– 29–

Тема НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

§1. Первообразная и неопределенный интеграл: основные определения и теоремы

В первом семестре мы подробно изучали операцию дифференцирования, которая играет важную роль, как в самом математическом анализе, так и в его приложениях. Не менее значительную роль играет и обратная операция – восстановление функции по ее производной. Эту операцию называют интегрированием.

Определение 1. Функция называется первообразной для функциина данном промежутке, если на этом промежутке выполняется равенство:

.

Например, для первообразная, ибо.

Всякий раз, когда математики вводят в рассмотрение операцию, обратную некоторой известной операции, возникают два вопроса:

1) всегда ли осуществима эта обратная операция?

2) однозначен ли результат этой операции?

Ответ на первый вопрос дает теорема существования первообразной, доказательство которой будет дано в теме «Определенный интеграл».

Теорема 1. Всякая непрерывная функция имеет первообразную.

Что касается второго вопроса, то ответ на него отрицательный: если у функции есть первообразная , то любая сумма , гдеconst будет первообразной для ,ибо , а. Интересен и такой пример: для функции первообразными являются функции ,и.Но в бесконечном множестве всех первообразных для любой функции существует определенный «порядок», устанавливаемый следующей теоремой.

Теорема 2. Пусть – некоторая первообразная для функции на промежутке .Тогда любая другая первообразная имеет вид ,где C – некоторая постоянная.

Доказательство. Вспомогательную функцию рассмотрим на промежутке и применим к ней теорему Лагранжа:

.

Но .Поэтому , т.е..Считая точку фиксированной, а точку – произвольной, получим const. Отсюда и следует, что , где – некоторая постоянная.

Определение 2. Совокупность всех первообразных для функции называется неопределенным интегралом от функции и обозначается символом .В этом обозначении: символ – знак интеграла, – подынтегральная функция, – подынтегральное выражение, x – переменная интегрирования.

Итак,

,

где , а – некоторая постоянная.

Отметим два свойства, непосредственно вытекающие из определения неопределенного интеграла:

, .

Неопределенный интеграл – это множество функций, и последнее равенство надо понимать так: производная каждой функции из этого множества совпадает с подынтегральной функцией.

С геометрической точки зрения неопределенный интеграл – это семейство кривых, каждая из которых получается путем сдвига одной из кривых вдоль оси .

Примем (пока без доказательства) два полезных свойства первообразных: 1) каждая первообразная нечетной функции – четна; 2) одна из первообразных четной функции – нечетна.

§2. Таблица основных интегралов

Равенство , равносильно равенству. Поэтому таблица интегралов – это таблица производных, прочитанная справа налево с некоторыми упрощениями и дополнениями.

1.,;;.

2..

3.;.

4..

5..

6..

7..

8..

9..

10..

11..

12.,.

13.,.

14.,,– “высокий” логарифм.

15.,, – “длинный” логарифм.

Всякую формулу интегрирования легко доказать дифференцированием. Например, формула 13:

.

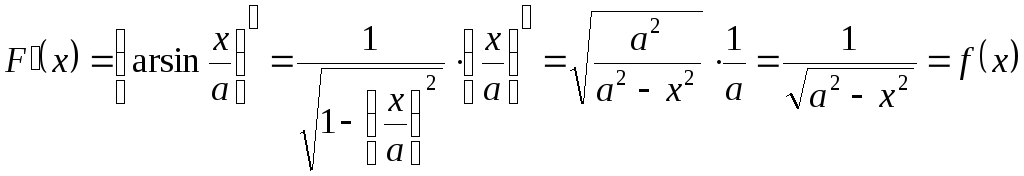Для простоты пишут вместоивместо.

Замечание. Учитывая свойства аркфункций, в формуле 12 вместо можно писать, а в формуле 13 вместописать.