–
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
Донецкий государственный технический университет методические указания
и задания к расчетно-графической работе
по разделу курса высшей математики
«МАТЕМАТИЧЕСКИЙ АНАЛИЗ.Часть 2»
(для студентов направления подготовки
и 6.030502 «Экономическая кибернетика»)
Раздел 1. Решение типовых задач
Таблица основных интегралов
1.
2.
.
3.
.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
1.1 Неопределённое интегрирование
Задача 1. Непосредственное интегрирование. Вычислить простейшие интегралы:
a)
b)
c)
d)
Решение. a) Простейшие изменения формулы записи подынтегральной функции приводят к табличному интегралу 14:
в) Раскрываем скобки, делим почленно числитель на знаменатель и используем линейность неопределённого интеграла ( интеграл от суммы равен сумме интегралов и постоянный множитель выносится за знак интеграла):
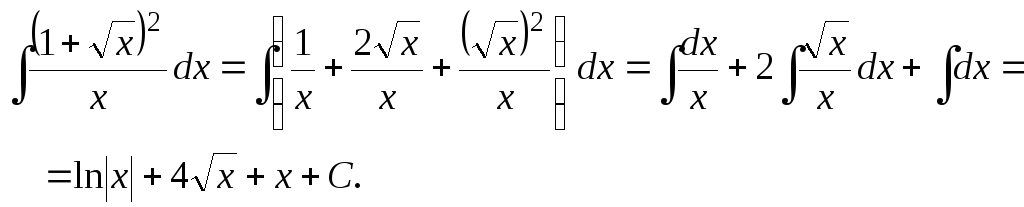
с) Этот интеграл
отличается от табличного интеграла 5
только тем, что в подынтегральной функции
переменная интегрирования
заменена линейной
функцией
.
Интегралы подобного вида будем называть
похожими на табличные. К ним применимо
следующее правило:
eсли
то
Итак, имеем
d) Выделение полного квадрата в подкоренном выражении знаменателя подынтегральной функции приводит нас к интегралу, похожему на табличный интеграл 13:
Задача 2.
Замена
переменной вида
.
Найти интегралы, используя метод
подведения под знак дифференциала:
-
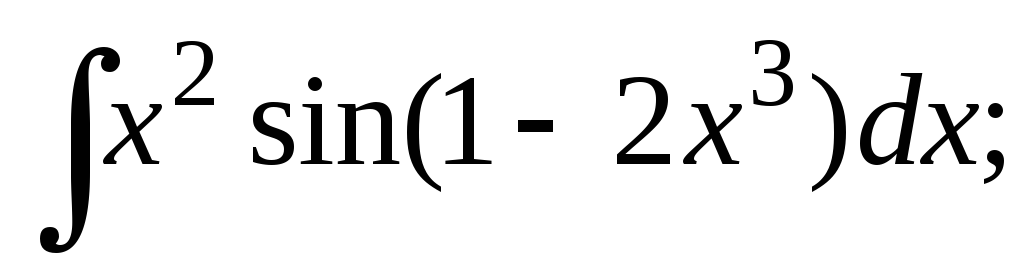b)
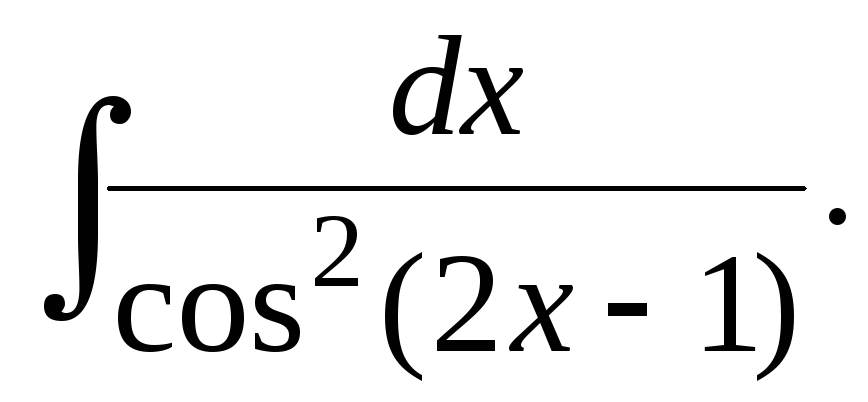
Решение.
a)
Чтобы выяснить вид функции
необходимо
представить подынтегральную функцию
в виде произведения сложной функции
и производной
и затем записать
в виде
.
В нашем случае:
-
Этот интеграл, вообще говоря, является похожим на табличный интеграл 6 и его можно вычислить, используя соответствующее правило. Или сделать замену:
,
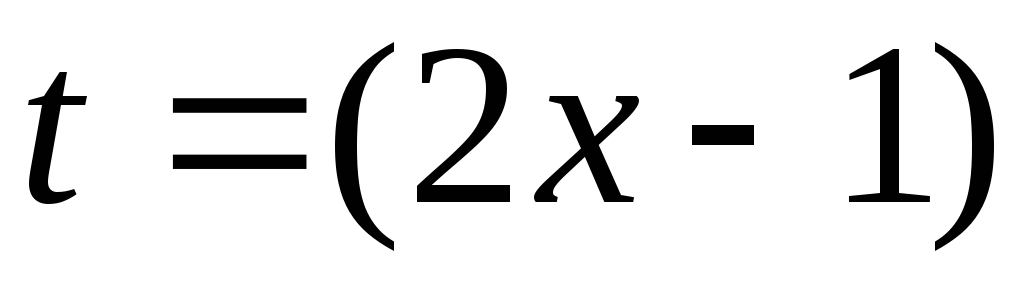тогда
,
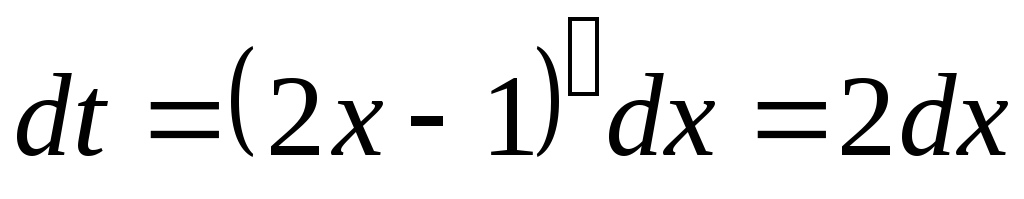откуда
.
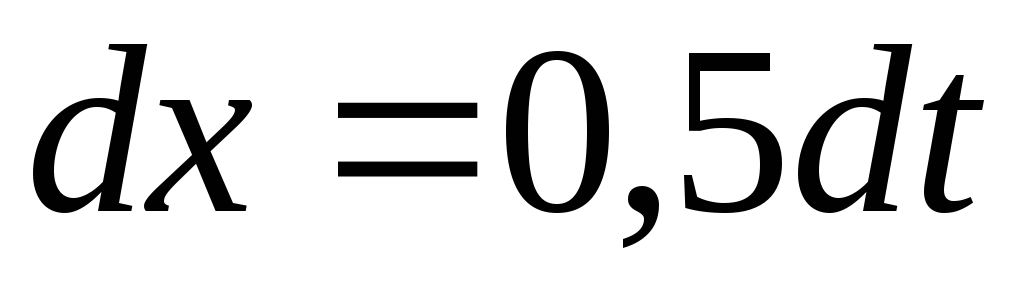Имеем для нашего интеграла:
Замечание 1. Вообще говоря, любую часть подынтегральной функции можно принять в качестве новой переменной. Например,
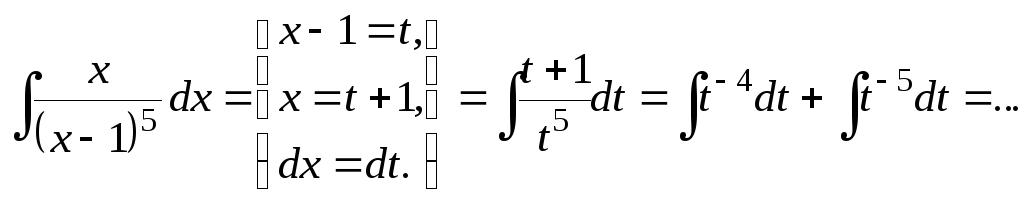
Сложность в таких
случаях состоит в том, что требуется
выразить
через
и найти
.
Замечание 2.
Второй вид замены переменной
,
где
– специально подобранная функция новой
переменной интегрирования, рассмотрим
в задачах 6
и 7.
Замечание 3. Делая в неопределенном интеграле замену переменной, не забывайте возвращаться к исходной переменой интегрирования.
Задача 3. Интегрирование по частям.
Вычислить интегралы:
a)
b)
c)
Решение. Метод интегрирования по частям базируется на формуле
Чтобы воспользоваться
этой формулой, необходимо подынтегральное
выражение представить в виде произведения
функции
,
для которой находим
,
и дифференциала
,
при этом функция
находится интегрированием:
.
Выбирая
и
,
необходимо руководствоваться двумя
требованиями: во-первых, интеграл
должен быть простым, а интеграл
– проще исходного
.
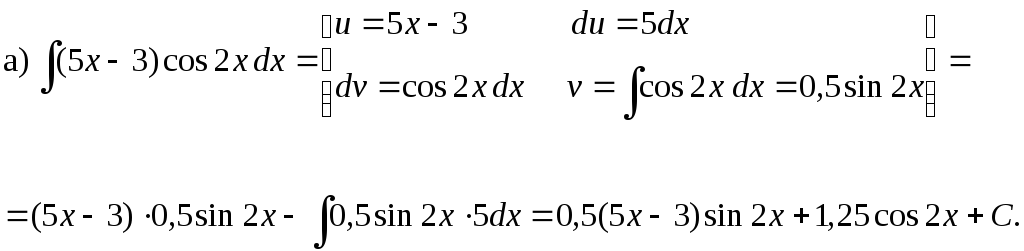
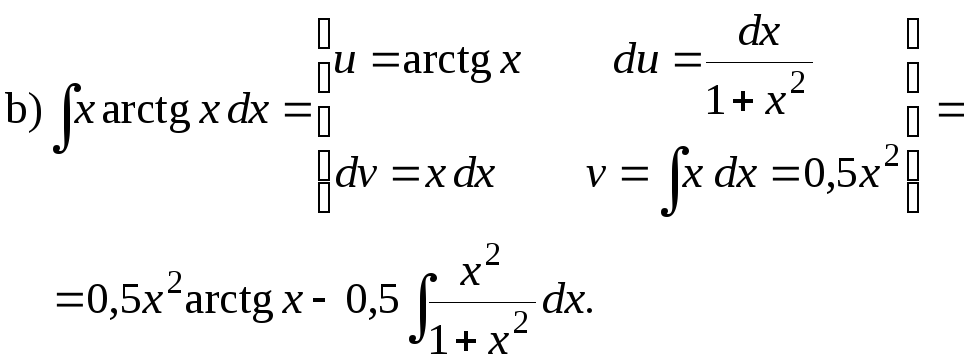
Функция
– это неправильная рациональная дробь.
Чтобы её проинтегрировать, необходимо
выделить целую часть путём деления
числителя на знаменатель «уголком». Но
в этом конкретном случае можно просто
в числитель добавить и вычесть единицу
и разделить почленно:
Окончательно:
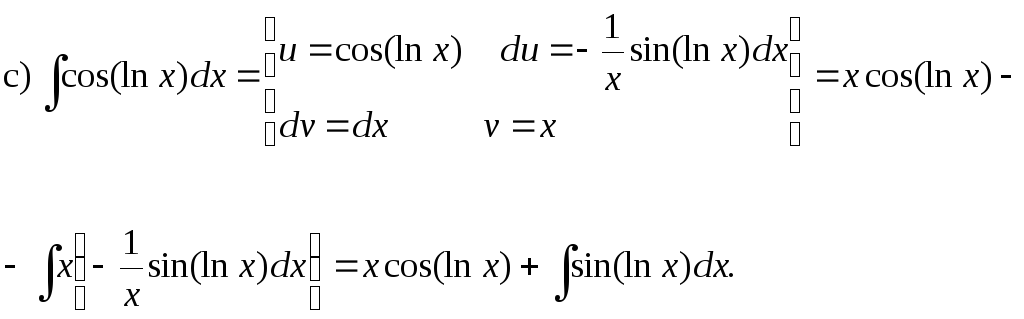
К получившемуся интегралу снова применяем метод интегрирования по частям
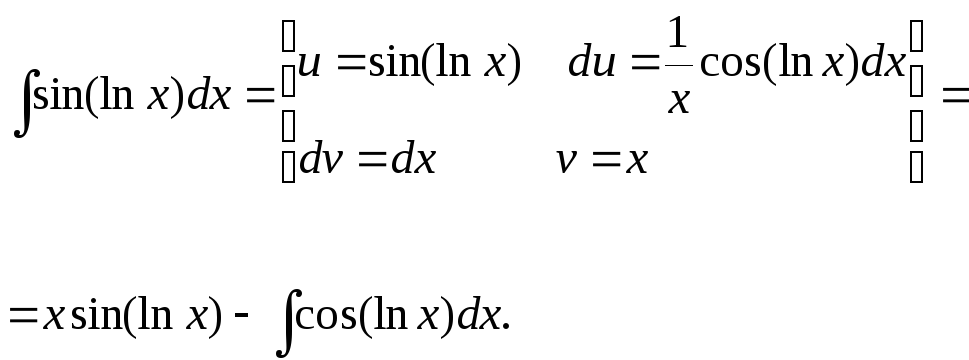
Обозначим искомый
интеграл
Тогда получим уравнение
.
Отсюда
.
Задача 4. Вычислить интегралы:
-
;
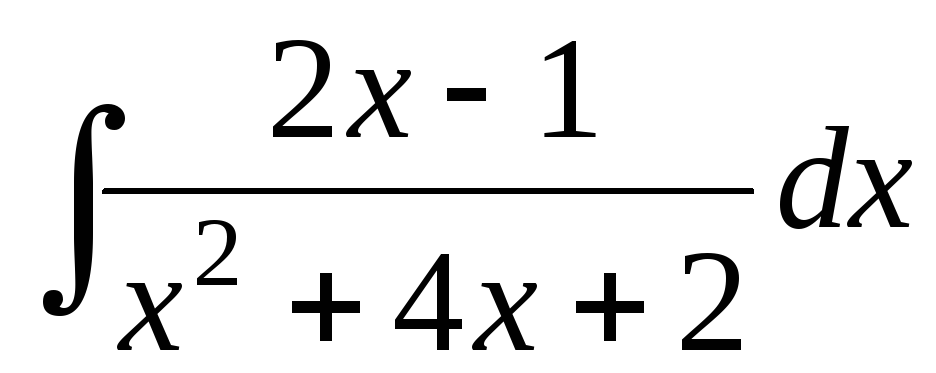b)
.
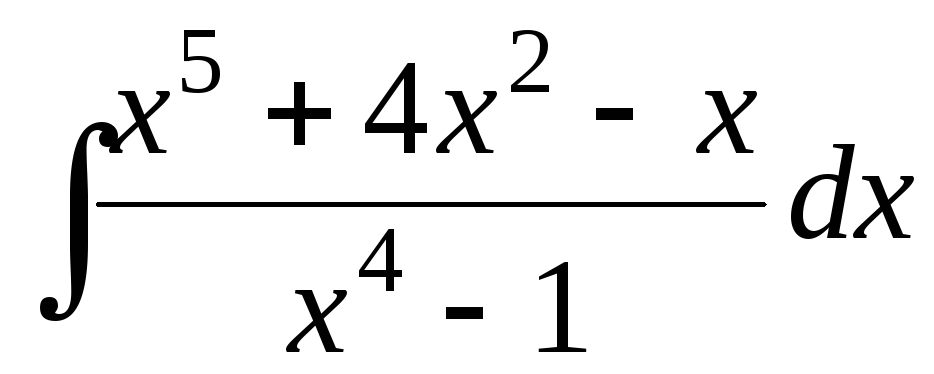Решение. a) В квадратном трёхчлене знаменателя подынтегральной функции выделяем полный квадрат и делаем замену переменной:
-
Подынтегральная функция – это неправильная рациональная дробь (отношение двух многочленов, причём степень числителя не меньше степени знаменателя). Выделяем целую часть этой дроби:
x
5
+4x2
– x
x4–1
x5–x x
4x2
Итак, для подынтегральной функции имеем
Второе слагаемое этой суммы (правильную дробь) можно разложить на простейшие дроби. Для этого сначала разложим знаменатель на множители
Такому разложению (два простых линейных множителей и один простой квадратичный множитель) соответствует такое формальное разложение на простейшие дроби:
.
В правой части этого равенства приведём сумму дробей к общему знаменателю и числитель полученной дроби приравняем числителю левой части:
Находим коэффициенты А, В, С и D. Сначала придадим переменной удобные значения:
Далее, приравняем
коэффициенты, стоящие при одинаковых
степенях
в левой и правой части:
Итак, окончательно имеем:
Теперь не трудно найти искомый интеграл:
Задача 5. Вычислить интегралы от тригонометрических выражений:
а)
b)
c)
Решение:
a)
Если подынтегральная функция такова,
что над тригонометрическими функциями
и
выполняются лишь
арифметические операции, то такой
интеграл рационализируется универсальной
тригонометрической подстановкой
.
Тогда
Для нашего интеграла имеем:
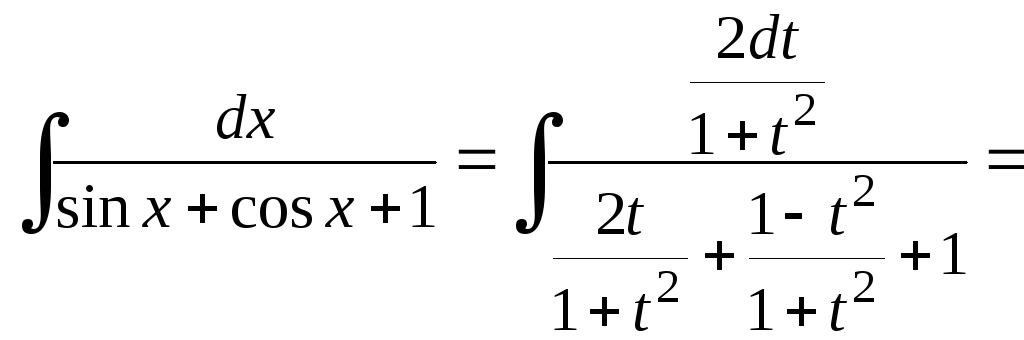
b)
Подстановка
в этом случае приводит к рациональной
функции сложного вида
Можно использовать
так называемую полууниверсальную
подстановку
(т.к.
и
входят в подынтегральную функцию в
чётных степенях). Тогда:
Но и при такой подстановке получим не совсем простую функцию
Лучше использовать формулы понижения степени:
Тогда
Получим для нашего интеграла:
с)
Используем основное тождество
и формулу синуса двойного угла
для преобразования подынтегральной
функции:
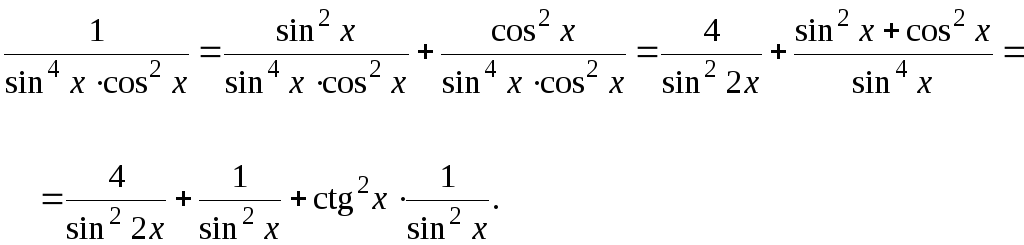
Находим интеграл:
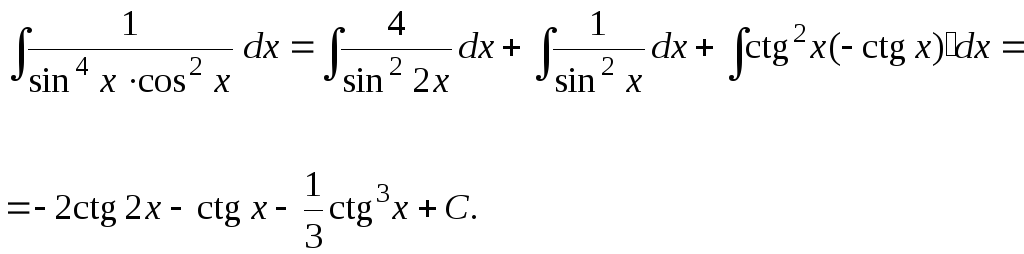
Задача 6. Найти интегралы путём приведения подынтегральных функций к рациональным функциям:
a)
b)
Решение:
а) Подкоренное выражение (одно и то же
в обоих корнях!) заменяем такой степенью
новой переменной, чтобы оба корня
извлеклись:
Тогда
и
.
Имеем для нашего интеграла:
в)
Некоторые (но не любые!) интегралы от
квадратичных иррациональностей, т.е.
содержащие радикалы вида
и
,
рационализируются простым и очевидным
образом: корень принимают в качестве
новой переменной интегрирования. В
нашем случае
Интеграл принимает вид:
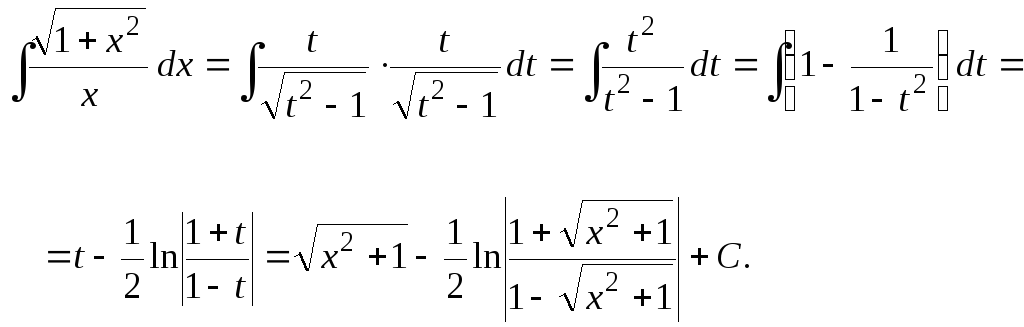
Задача 7. Найти интегралы, используя тригонометрические или гиперболические подстановки:
а)
b)
.
Решение:
а) Область определения подынтегральной
функции состоит из двух частей
.
Вообще говоря, в таком случае первообразная
может иметь разные выражения в этих
частях. Но данная подынтегральная
функция – чётная, следовательно, одна
из первообразных должна быть нечётная.
Рассмотрим случай
.
Заметим сразу, что замена
не приводит к «уничтожению» радикала
(убедитесь сами). Здесь переменную
интегрирования
необходимо заменить такой функцией
,
чтобы разность
была бы квадратом некоторой другой
функции. Например, пусть
,
причём
.
Тогда:
Получим для интеграла
Ответ можно
упростить, если воспользоваться известной
формулой
,
откуда
Итак, имеем для
Но функция
– нечётная, значит, полученный ответ
справедлив для всех
.
в) Радикал вида
можно «уничтожить» подстановкой
.
Но для данного конкретного интеграла
получим сложное для интегрирования
тригонометрическое выражение. Лучше
воспользоваться гиперболической
подстановкой
.
Тогда
Для данного интеграла получим
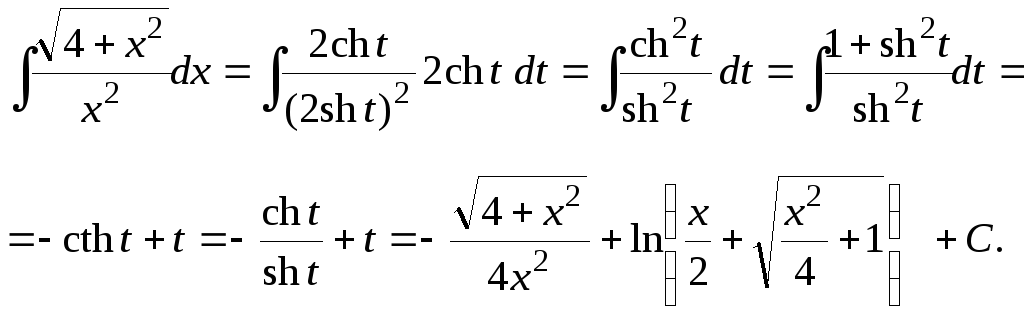
Замечание 4.
Радикалы вида
можно уничтожить подстановкой
или
,
причём для
.
Для других значений
лучше
всего использовать чётность– нечётность подынтегральной функции.
Задача 8. Найти интегралы, используя подстановки Чебышева и Эйлера:
а)
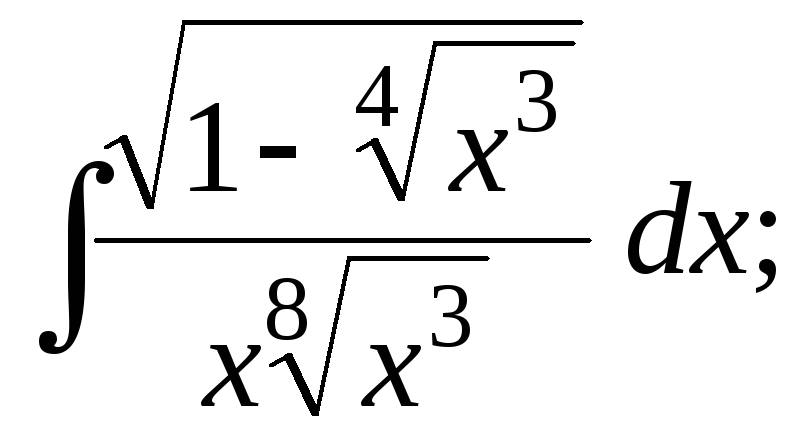b)
Решение. а) Подстановки Чебышева используются для интегрирования выражений вида (т.н. биномиальные дифференциалы)
,
где
–
рациональные числа. Если данную
подынтегральную функцию переписать в
стандартной форме, получим
т.е.
.
При этом число
– целое, значит, применима третья
подстановка Чебышева. Новая переменная
интегрирования
вводится соотношением
,
где
– знаменатель дроби
.
Предварительные вычисле-ния
для данного интеграла таковы:
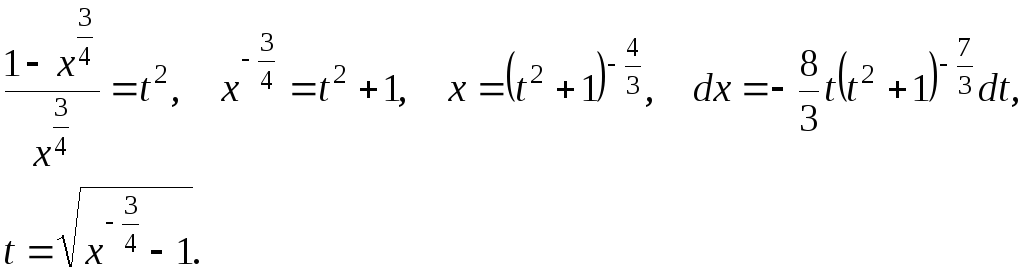
Получим для интеграла:
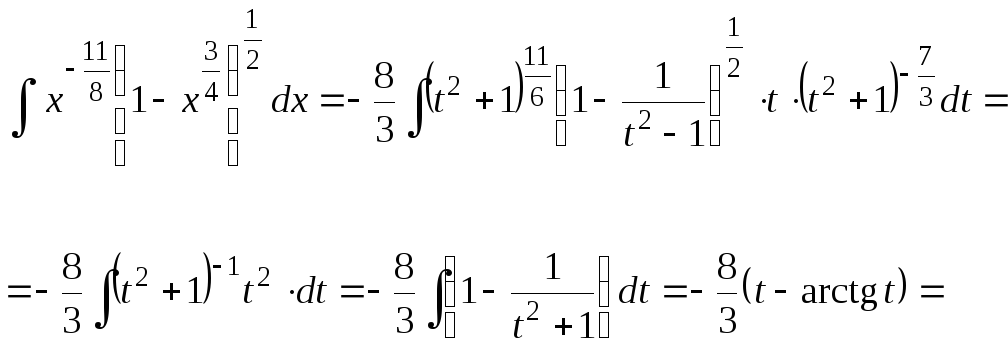
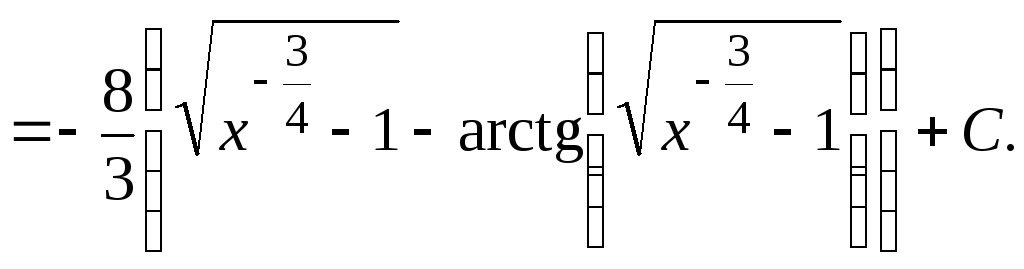
Замечание 5. Приведём ещё два случая интегрируемости биномиальных дифференциалов:
1)
2)
где
– знаменатель дроби
,
– НОК знаменателей дробей
и
.
b)
Подстановки Эйлера применяются для
рационализации интегралов, содержащих
квадратичную иррациональность
.
В нашем случае
,
поэтому применяем 1ю
подстановку
Эйлера. Новая переменная интегрирования
вводится соотношением
.
Предварительные вычисления:
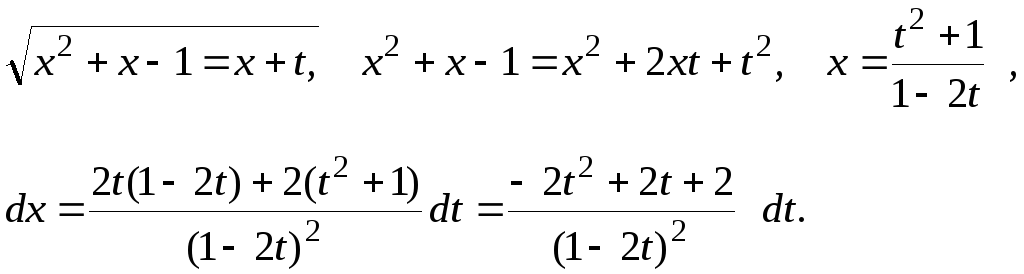
Имеем для интеграла:
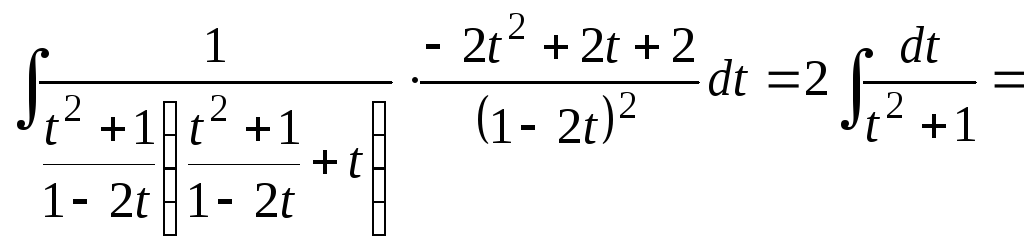
Замечание
6. Ещё две
подстановки Эйлера:
1)
2)
где
–
один из корней квадратного трёхчлена.