МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ

Министерство образования и науки Российской Федерации ГОУ ВПО «Тамбовский государственный технический университет»

МАТЕМАТИЧЕСКИЙ

ПРАКТИКУМ

І КУРС

Учебные задания для студентов 1 курса инженерных и экономических специальностей

Тамбов Издательство ТГТУ 2011

УДК 5(075.8) ББК В11я73-5

М-34

Утверждено редакционно-издательским советом университета

Рецензенты:

Доктор физико-математических наук, профессор кафедры РВС ТГТУ

С.М. Дзюба

Доктор физико-математических наук, профессор кафедры алгебры и геометрии ТГУ им. Г.Р. Державина

А.И. Булгаков

Составители:

А.В. Медведев, И.В. Петрова, В.А. Попов, Н.П. Пучков, А.И. Урусов, А.В. Щербакова

Математический практикум. І курс: Учебное пособие. / Сост.: А.В. Медведев, И.В. Петрова, В.А. Попов, Н.П. Пучков, А.И. Урусов, А.В. Щербакова. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2011. 191 с.

Даны задания по основным разделам учебных программ для технических и экономических специальностей, при этом они сопровождаются кратким теоретическим материалом и методами решения основных задач. Предложенные задачи являются типовыми, предназначены для аудиторной и самостоятельной работы студентов, и могут служить основой при составлении вариантов проверочных заданий.

Предназначено для студентов 1 курса инженерных и экономических специальностей.

УДК 5(075.8) ББК В11я73-5

© ГОУ ВПО «Тамбовский государственный

технический университет» (ТГТУ), 2011

1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.

1.1. Матрицы. Определители.

Числовой матрицей размерности m × n называется прямоугольная таблица, состоящая из m -строк и n -столбцов, на пересечении которых стоят числа, называемые элементами матрицы.

Матрицы принято обозначать большими латинскими буквами, а элементы

– соответствующими строчными буквами с индексами. Первый индекс указывает номер строки, а второй – номер столбца в котором стоит элемент. Если нужно указать размерность матрицы, то после обозначения матрицы через тире будем указывать эту размерность.

Две матрицы A = (aij ) (размерности m × n ) и B = (bij ) (размерности m1 n1 ) называются равными, если они имеют одинаковую размерность и равны их

элементы, стоящие на одинаковых местах, т.е. если:		a)m = m1,n = n1 ; b)
Равенство aij = bij справедливо для всех i, j таких, что i =1,m; j =1,n.
Если A = (aij ) – матрица размерности m × n	и m = n , то					матрица

называется квадратной, в противном случае матрица называется

прямоугольной.

Матрица, все элементы которой равны нулю, называется нулевой. Эту матрицу далее будем обозначать буквой O .

Матрица AT называется транспонированной по отношению к матрице A, если строки матрицы A являются столбцами матрицы AT с соответствующими

номерами, т.е. первая строка матрицы

A является первым столбцом матрицы

AT , вторая строка матрицы A является вторым столбцом матрицы AT , и т.д.

a

a

...

a

a

a

...

a

11

12

1n

11

21

m1

Таким образом, если

a21

a22 ...

a2n

T

a12

a22

...

am2

A = L

, то

A

= L

.

am2 ...

a2n

...

am1

amn

a1n

amn

Количество строк (которое равно количеству столбцов) квадратной матрицы называется порядком этой матрицы.

Главной диагональю квадратной матрицы называется диагональ, на которой расположены элементы aii . Другая диагональ матрицы называется

побочной диагональю.

Квадратная матрица называется диагональной, если aij = 0 для всех i, j

таких, что i ≠ j .

Квадратная матрица, у которой элементы, стоящие на главной диагонали равны 1, а остальные равны нулю, называется единичной матрицей.

Далее единичную матрицу будем обозначать буквой I .

Матрица A называется верхней треугольной матрицей, если aij = 0 для всех i, j таких, что i > j .

3

Матрица

A называется нижней треугольной матрицей, если

aij = 0

для

всех i, j таких, что i < j .

2

− 3

− 2

4

2

0

0

− 6

0 −1

Примеры матриц.

A =

4

; B =

0

;

; C =

−1

− 2

− 7

3

0

0

8

2

7

− 2

−1

0

0

1 0 0

D = 0 −1

3 ; F =

6

4

0 ;

I =

0 1 0 .

0

9

0 0 1

0 − 5

− 3 − 5

Здесь

A

–

прямоугольная

матрица размерности

3×2;

B

–

квадратная

матрица порядка 2; C – диагональная матрица; D – верхняя треугольная

матрица; F – нижняя треугольная матрица; I – единичная матрица.

Пусть далее матрицы

A = (aij ) и B = (bij ) - матрицы размерности m × n , а

α - некоторое число.

Матрица D = (dij )

размерности m × n элементы которой вычисляются по

формуле

dij = aijα , называется

произведением

матрицы A на число α и

обозначается

Aα . Таким образом

все элементы матрицы

Aα

получаются

умножением соответствующих элементов матрицы A на число α . Аналогично

def

определяется матрица αA: αA = (αaij ) .

Матрица

(−1) A = (−aij ) называется

противоположной

матрице

A и

обозначается

− A.

Матрица D = (dij )

размерности m × n элементы которой вычисляются по

формуле dij = aij

+ bij , называется суммой матриц A и B и обозначается A+ B .

Разность

матриц

A

и

B обозначается

как

A− B

и

определяется

def

формулой A− B = A+ (−1) B.

Пусть α, β - числа, A,B,C - матрицы размерности m × n . Тогда, используя свойства числовых операций и вышеприведенные определения, легко доказать справедливость следующих равенств:

A− A = O , A+ O = A, A+ B = B + A, A+ (B + C) = (A+ B) + C , αA = Aα ,

α(A+ B) = αA+αB ,	(α + β )A = αA+ βA,	(αβ)A = α(βA) . При этом
предполагается, что все рассматриваемые операции определены.
Пусть матрицы	A = (aij ) и B = (bij ) - матрицы размерности m × n и n × k

соответственно. Т.е. количество столбцов первой матрицы равно количеству строк второй.

Матрица D = (dij ) размерности m × k , элементы которой определяются равенством

def	n
dij =	∑ais bsj = ai1 b1 j + ai2 b2 j +... + ain bnj
	s=1

называется произведением матриц A и B обозначается как A B или как AB.

4

Справедливы следующие равенства (предполагаем, что соответствующие операции выполнимы): A I = A, I A = A, (AB)C = A(BC), (A+ B)C = AC + BC ,

A(B + C) = AB + AC , α(AB) = (αA)B = A(αB).

Обратим внимание на следующее обстоятельство: если оба произведения

AB и BA существуют, то вообще говоря AB ≠ BA.

1

−1

−1

2

Пример 1. Пусть даны матрицы

0

2

×3;

B =

3

-

A =

-

1

2

− 3 − 2

0 −1

3 − 4

. Так как размерность матрицы

AB равна 2 2, а

3×2; C =

- 2 2

1

2

матрицы BA - 3×3, то A B ≠ B A.

Вычислим

матрицу

D = A B − 2 C .

Сначала

(в

соответствии

с

определением произведения матриц) вычисляем A B .

1

−

1

−1

2

0

3

=

A B =

1

2 − 3

− 2

0

−1

1 (−1) + 0 3+ (−1) 0

1 2 + 0

1+ (

−1)

(−1)

−1

3

=

=

.

(−1) + (−3) 3+ (−2)

0 2 2 + (−3)

1+ (−2) (−1)

−11

2

3

Затем находим 2 C :

2 3

2 (−4)

6

−8

2 C =

=

.

2 1

4

2 2

2

Теперь можно вычислить D :

−1

3

6 −8

−

7 11

D =

−

=

.

−11

3

2

4

−13

−1

Квадратная

матрица

A

порядка

n

называется

обратимой,

если

существует такая матрица D порядка n что D A = I . В этом случае матрица D называется обратной к матрице A.

Матрица,	обратная к матрице A обозначается	A−1. Справедливы
следующие утверждения.
Теорема.	Если матрица A обратима, то обратима	и матрица A−1 и
(A−1)−1 = A.

Теорема. Если матрица A обратима, то A−1 A = A A−1 = I .

Каждой квадратной матрице по определенному закону можно поставить в соответствии число, которое называется определителем этой матрицы.

Если A = (aij )− матрица размерности n × n , то определитель этой матрицы обозначается либо det A, либо

5

	a11	a12	L a1n
	a21	a22	K a2n	.
	. . . . . . .
	an1	an2	L ann

Дадим определение определителя для матриц различной размерности.

def

• Пусть A = (a11 )−1 1 , тогда det A = a11 .

• Пусть A = (aij )− 2 2 , тогда

a

a

def

a

− a

a

det A =

11

12

= a

22

21

.

a21

a22

11

12

• Пусть A = (aij )− 3 3 , тогда

a11

a12

a13

def

det A =

a21

a22

a23

= (a11 a22 a33 + a12 a23 a31 + a13 a21 a32 )−

a31

a32

a33

− (a13 a22 a31 + a12 a21 a33 + a11 a23 a32 ).

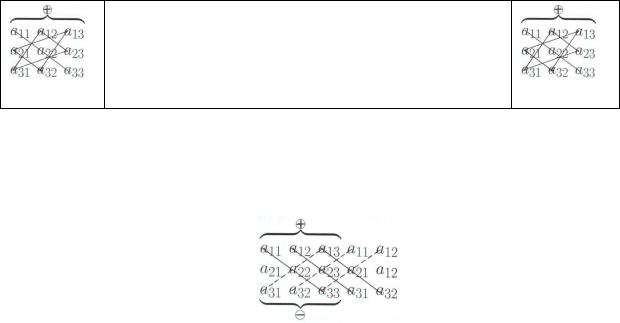
Чтобы запомнить последнюю формулу можно воспользоваться правилом треугольников: слагаемые, заключенные в первую пару круглых скобок, получены путем перемножения элементов, стоящих на главной диагонали, (первое слагаемое), а текже перемножением элементов, стоящих в вершинах треугольников, основания которых параллельны главной диагонали (два других слагаемых). Аналогично получены слагаемые, заключенные во вторую пару круглых скобок: первое слагаемое - произведение элементов, стоящих на побочной диагонали, а два других слагаемых - произведение элементов, стоящих в вершинах треугольников, основания которых параллельны побочной диагонали.

На рисунке слева схематически указано правило вычисления первой группы слагаемых,

а справа - второй группы слагаемых.

При некоторой тренировке вычисление определителя матрицы третьего порядка производится достаточно быстро.

Можно воспользоваться также правилом Саррюса (приписыванием двух первых столбцов), которое ясно из нижеследующего рисунка :

6

Пусть A = (aij ) - матрица размерности n × n . Минором Mij элемента aij

(минором Mij соответствующим элементу aij ) называется определитель матрицы, полученной из матрицы A вычеркиванием i -ой строки и j -ого столбца. Алгебраическим дополнением Aij элемента aij (алгебраическим дополнением Aij соответствующим элементу aij ) называется величина

(−1)i+ j M	ij	, т.е. A = (−1)i+ j M		ij	.
		ij
Теперь дадим			определение			определителя	для матрицы	произвольной
						def
размерности n × n , где n ≥ 2 : det A = ∑ns=1a1s A1s .
(Эта		формула	называется			формулой	вычисления	определителя

разложением по элементам 1-ой строки).

Легко показать, что это определение не противоречит предыдущим определениям.

Свойства определителей. Далее строку или столбец будем называть «ряд». 1. При транспонировании, т.е. при замене каждой строки определителя

столбцом с тем же номером, определитель не меняется.

Пример 2.	Пусть	1		2		1		3
		A =			, тогда	AT =			. Легко проверить, что
			3	4			2	4

detA = detAT .

2. При перестановке двух строк или двух столбцов определитель лишь меняет знак.

Пример 3. Очевидны следующие равенства:	1	2	=	−	2	1	;	1	2	=
	3	4			4	3		3	4

−3 4 .

1 2

3.Если все элементы некоторого ряда равны нулю, то и определитель равен нулю.

4.Если элементы какого-либо ряда умножить на одно и то же число, то и определитель умножится на это число.

		2		1 (−2)	2 (−2)		1	2	(−2)		.
Пример 4. − 2	1		=			=
	3	4		3	4		3	4	(−2)

Обратите внимание на следующее: при умножении матрицы на число надо все элементы этой матрицы умножить на данное число, если же умножаем определитель на число, то на это число надо умножить элементы

какого-либо одного ряда!
5.	Если элементы двух параллельных рядов пропорциональны, то
определитель равен нулю.
			2		1	2		= 7		1	2
Пример 5.		1		=								= 0.
		7	14		7 1	7 2				1	2
6.	Если каждый			элемент		k-ого ряда						определителя представляет собой

7

сумму двух слагаемых, то этот определитель может быть представлен в виде суммы двух определителей, первый из которых имеет в k-ом ряду первые из упомянутых слагаемых, а второй имеет в k-ом ряду вторые из упомянутых слагаемых, в остальных рядах эти определители имеют те же элементы, что и

исходный определитель.

Пример 6.

		5		=		1+ (−1) 2 + 3			=		1	2		+		−1 3			= (4 − 6) + (−4 − 9) = −15 .
−15 =	0
	3	4				3	4				3	4				3	4

7. Если элементы какого-либо ряда умножить на одно и то же число и прибавить к соответствующим элементам другого параллельного ряда, то

определитель не изменится.
Пример 7. Легко проверить равенство		2		=		1	0		. Здесь второй
	1
	3	4				3	− 2

определитель получен из первого умножением элементов первого столбца на -2

	и прибавлением к соответствующим элементам второго столбца, т.е.										1	2	=
											3	4
			2 +1 (−2)		=		1	0		.
		1
		3	4 + 3 (−2)				3	− 2

8. Сумма произведений элементов некоторого ряда на алгабраические дополнения этих элементов равна определителю. Т.е. справедливы равенства (в скобках приведено название этих формул):

det A = ∑ns=1ais Ais (вычисление определителя разложением по элементам i- ой строки).

det A = ∑ns=1asj Asj (вычисление определителя разложением по элементам j-

ого столбца).

Пример 8. Вычислим определитель некоторой матрицы разложением по элементам первой строки.

− 2 4 3

− 3	9		6 = −2 A11 + 4 A12 + 3 A13 =
− 7	3		4
= −2 (−1)1+1 M						11	+ 4 (−1)1+2 M					12		+ 3 (−1)1+3	M	13	=
			6		− 3			6		− 3	9
= −2		9		− 4					+ 3				= −2 (36 −18) − 4 (−12 + 42) + 3 (−9 + 63) =
		3	4		− 7			4		− 7	3

= −36 −120 +162 = 6.

Таким же образом можно вычислять определители разложением по любому столбцу или по любой строке.

9. Сумма произведений элементов некоторого ряда на алгабраические дополнения соответствующих элементов другого параллельного ряда равна нулю.

8

Т.е. ∑ns=1ais Ajs = 0 , ∑ns=1asj Asi = 0 , если i ≠ j .

Вычисление определителя получением нулей в какой-либо строке или какомлибо столбце.

Умножая элементы строк или столбцов на определенные множители, а затем складывая строки или столбцы, можно добиться того, что все элементы некоторого ряда, за исключением одного, будут равны нулю, а тогда вычисление исходного определителя сводится к вычислению одного определителя меньшего порядка. Таким образом, систематическое применение сначала седьмого свойства определителей, а затем восьмого свойства определителей позволяет свести вычисление определителя n -ого порядка к вычислению одного определителя (n −1) -ого порядка, вычисление которого в свою очередь можно свести к вычислению определителя (n − 2)-ого порядка и т.д.

Договоримся о следующих обозначениях. Если элементы какого-либо ряда будем умножать на число, то это число будем записывать в круглых скобках напротив этого ряда, а стрелочкой, направленной к другому параллельному ряду, будем показывать к соответствующим элементам какого ряда будем

прибавлять полученные произведения.
		2	− 3		1	2	− 3+1 3		1	2	0
	1
Пример 9.	− 2	3	4	=	− 2	3	4 − 2 3	=	− 2	3	− 2	.
	3	− 4	5		3	− 4	5+ 3 3		3	− 4	14
(3)			↑

Пример 10.

1	2	− 3		(−2)		1	2	− 3		1	2	− 3
− 2	3	4			=	− 2	3	4	=	− 2	3	4		.
3	− 4	5		←		3+1 (−2)	− 4 + 2 (−2)	5− 3 (−2)		1	− 8	11

В примере 9 элементы 1-ого столбца умножаем на 3 и прибавляем к соответствующим элементам 3-его столбца, а в примере 10 - элементы 1-ой строки умножаем на -2 и прибавляем к соответствующим элементам 3-ей строки.

Из 7-го свойства определителей следует, что если элементы i-ого ряда умножить на одно и то же число и прибавить к соответствующим элементам j- ого параллельного ряда, затем элементы i-ого ряда умножить на одно и то же число и прибавить к соответствующим элементам k-ого параллельного ряда, то определитель не изменится (предполагаем, что числа i,j,k попарно не равны друг другу). Т.е. элементы какого-то выбранного ряда можно умножать на различные множители и прибавлять к соответствующим элементам других параллельных рядов, при этом величина определителя не изменится. Например, далее показано что элементы первого столбца умножили на 3 и прибавили к соответствующим элементам второго столбца, затем вновь элементы первого столбца умножили на 2 и прибавили к соответствующим элементам третьего

9

столбца, после чего применили формулу вычисления определителя разложением по элементам второй строки.

− 2 4 3

− 2 4 − 2 3

3− 2 2

det A =

− 3

9 6

=

− 3 9 − 3 3

6 − 3 2

=

− 7 3 4

− 7 3− 7 3

4 − 7 2

(3)

↑

(2)

↑

− 2

− 2

−1

= −3 (−1)2+1

− 2

−1

=

− 3

0

0

= −3

A + 0

A + 0 A

= 6.

21

22

23

−18

−10

− 7

−18

−10

Вычислим определитель этой же матрицы получением нулей во втором столбце и последующим разложением по элементам этого столбца.

	− 2	4	3		←
det A =	− 3	9	6			← =
	− 7	3	4		(−1)	(−3)

=(умножим	элементы	третьей строки на	-1 и прибавим к
соответствующим	элементам	первой строки, затем	умножим элементы

третьей строки на -3 и прибавим к соответствующим элементам второй строки)=

		1	−1		(−3)
	5
=	18	0	− 6			=
	− 7	3	4				←
=(теперь			умножим элементы первой строки на -3 и прибавим к
соответствующим элементам третьей строки)=
		1	−1
	5
=	18	0	− 6				=
	− 22	0	7

=(применяем формулу вычисления определителя разложением по

элементам второго столбца)=
=1 A + 0 A + 0 A = (−1)1+2									− 6		=
			M	12	= −M	12	= −	18
12	22	32						− 22	7

=− (18 7 − (−22) (−6)) = 6.

Вобщем случае алгоритм получения нулей в j-ом столбце выглядит

следующим образом: в j-ом столбце выбираем какой-нибудь элемент, который отличен от нуля. Пусть это будет akj , т.е. akj ≠ 0 . Тогда все элемнты строки, в

которой находится выбранный элемент (в нашем случае это k-ая строка) умножаем на (−asj/akj ) и прибавляем к соответствующим элементам s-ой

строки (s ≠ k) , в результате в s-ой строке в j-ом столбце получаем нуль.

10