ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение Высшего профессионального образования

¾Тамбовский государственный технический университет¿

Элементы линейной алгебры

Учебно-методические рекомендации для студентов 1 курса заочного отделения

Тамбов 2010

УДК 512.64 ББК В143я73-2 У73

Утверждено Редакционно-издательским советом университета

Р е ц е н з е н т д.ф.-м.н. А.И. Булгаков

С о с т а в и т е л ь А.И. Урусов

У73 Элементы линейной алгебры. Учебно-методические рекомендации для студентов 1 курса заочного отделения. / Сост. А. И. Урусов. Тамбов: Изд-во Тамб. Гос. Техн. Ун-та, 2010. 18 с.

Кратко изложены основные понятия теории матриц и определителей. Приведены три метода решения систем линейных алгебраических уравнений. Основные понятия и методы сопроваждаются примерами, поясняющими эти понятия и методы. Предназначены для студентов 1 курса технических специальностей заочного отделения.

c ГОУ ВПО "Тамбовский государственный технический университет"(ТГТУ), 2010

Сводка обозначений и соглашений.

R множество вещественных чисел.

A = B из утверждения A следует утверждение B.

def

A = B выражение B является определением A.

Матрицы обозначаются большими латинскими буквами, а элементы этих матриц соответствующими строчными буквами с индексами.

O нулевая матрица.

I единичная матрица.

AT матрица, транспонированная по отношению к матрице A. A−1 матрица, обратная к матрице A.

DET A определитель матрицы A.

Матрицы.

Далее рассматриваем только вещественные числа, т.е. элементы множества R.

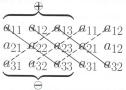
Определение. Числовой матрицей размерности m ×n называется прямоугольная таблица, состоящая из m-строк и n-столбцов, на пересечении которых стоят числа, называемые элементами матрицы.

Матрицы принято обозначать большими латинскими буквами, а элементы соответствующими строчными буквами с индексами. Первый индекс указывает номер строки, а второй номер столбца в котором стоит элемент. Если нужно указать размерность матрицы, то после обозначения матрицы через тире будем указывать эту размерность.

Примеры.

A = (aij ) − m × n Матрица A размерности m × n, aij элементы этой матрицы, i номер строки, в которой стоит элемент aij ; j номер столбца, в котором стоит элемент aij .

B = (bij ) =	−2	−1	−9	. Это матрица размерности 2 × 3, b11 = −3, b12 = 0, b13 = 7, b21 = 2,
	3	0	7

b22 = −1, b23 = −9.

Определение. Две матрицы A = (aij ) (размерности m × n) и B = (bij ) (размерности m1 × n1) называются равными, если они имеют одинаковую размерность и равны их элементы, стоящие на одинаковых местах, т.е. если: a) m = m1, n = n1; b) Равенство aij = bij справедливо для всех i, j таких, что i = 1, m; j = 1, n.

Определение. Если A = (aij ) матрица размерности m × n и m = n, то матрица называется квадратной, в противном случае матрица называется прямоугольной.

Определение. Матрица, все элементы которой равны нулю, называется нулевой. Эту матрицу далее будем обозначать буквой O.

Определение. Матрица AT называется транспонированной по отношению к матрице A, если строки матрицы A являются столбцами матрицы AT с соответствующими номерами, т.е. первая строка матрицы A является первым столбцом матрицы AT , вторая строка матрицы A является вторым столбцом матрицы AT , и т.д.

a11

a12

...

a1n

, то AT =

a11

a21

...

am1

.

Таким образом, если A =

a21

a22

...

a2n

a12

a22

...

am2

am

1

am

2

...

amn

a n

a

n

...

amn

1

2

. . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . .

Определение. Количество строк (которое равно количеству столбцов) квадратной матрицы называется порядком этой матрицы.

Определение. Главной диагональю квадратной матрицы называется диагональ, на которой расположены элементы aii. Другая диагональ матрицы называется побочной диагональю.

Определение. Квадратная матрица называется диагональной, если aij = 0 дла всех i, j таких, что i 6= j.

Определение. Квадратная матрица, у которой элементы, стоящие на главной диагонали равны 1, а остальные равны нулю, называется единичной матрицей.

Далее единичную матрицу будем обозначать буквой I.

Определение. Матрица A называется верхней треугольной матрицей, если aij = 0 дла всех i, j таких, что i > j.

3

Определение. Матрица A называется нижней треугольной матрицей, если aij = 0 дла всех i, j таких, что i < j.

Примеры матриц. A =					−6	4	; B =		−7	3	; C =			0	−1	0	;
					2	−3				4				2	0	0
					−1	−2								0	0	8
									−2
D =	2	7	−2			−1		0	; I =		0 1
	0	−1	3	; F =		6	4						0 .
							0	0			1	0	0
	0	0	−5			9	−3	−5			0	0	1

Здесь A прямоугольная матрица размерности 3 × 2; B квадратная матрица порядка 2; C диагональная матрица; D верхняя треугольная матрица; F нижняя треугольная матрица; I единичная матрица.

Операции над матрицами.

Умножение матрицы на число и сложение матриц.

Пусть далее матрицы A = (aij ) и B = (bij ) - матрицы размерности m × n, а α - некоторое число. Определение. Матрица D = (dij ) размерности m × n элементы которой вычисляются по формуле

dij = aij α, называется произведением матрицы A на число α и обозначается Aα. Таким образом все элементы матрицы Aα получаются умножением соответствующих элементов матрицы A на число α.

def

Аналогично определяется матрица αA: αA = (αaij ).

Определение. Матрица (−1) · A = (−aij ) называется противоположной матрице A и обозначается

−A.

Определение. Матрица D = (dij ) размерности m × n элементы которой вычисляются по формуле dij = aij + bij , называется суммой матриц A и B и обозначается A + B.

def

Разность матриц A и B обозначается как A − B и определяется формулой A − B = A + (−1) · B. Пусть α, β - числа, A, B, C - матрицы размерности m × n. Тогда, используя свойства числовых

операций и вышеприведенные определения, легко доказать справедливость следующих равенств:

A − A = O, A + O = A, A + B = B + A, A + (B + C) = (A + B) + C, αA = Aα, α(A + B) = αA + αB,

(α + β)A = αA + βA, (αβ)A = α(βA). При этом предполагается, что все рассматриваемые операции определены.

Умножение матриц.

Пусть матрицы A = (aij ) и B = (bij ) - матрицы размерности m × n и n × k соответственно. Т.е. количество столбцов первой матрицы равно количеству строк второй.

Определение. Матрица D = (dij ) размерности m ×k, элементы которой определяются равенством

n

def X

dij = ais · bsj = ai1 · b1j + ai2 · b2j + ... + ain · bnj s=1

называется произведением матриц A и B обозначается как A · B или как AB.

Справедливы следующие равенства (предполагаем, что соответствующие операции выполнимы):

A·I = A, I·A = A, (AB)C=A(BC), (A+B)C = AC+BC, A(B+C) = AB+AC, α(AB) = (αA)B = A(αB). Обратим внимание на следующее обстоятельство: если оба произведения AB и BA существуют, то

вообще говоря AB =6 BA.
			1	0	−1	- 2 × 3; B =		−1	2	- 3 × 2; C =
	Пример. Пусть даны матрицы A =							3	1
			2	−3	−2
								0	−1
	3	−4
	1	2 - 2 ×2. Так как размерность матрицы AB равна 2 ×2, а матрицы BA - 3 ×3, то A ·B 6= B ·A.
	Вычислим матрицу D = A·B −2 ·C. Сначала (в соответствии с определением произведения матриц)
вычисляем A · B.
			1	0 −1		−1	2
		A · B =			·	3	1 =
			2 −3 −2
						0	−1

4

=	1 · (−1) + 0 · 3 + (−1) · 0			1 · 2 + 0 · 1 + (−1) · (−1)				=	−1	3
	2 · (−1) + (−3) · 3 + (−2) · 0 2 · 2 + (−3) · 1 + (−2) · (−1)								−11	3
.
Затем находим 2 · C:
	2	3	2		(−4)	6	−8
	2 · C = 2 ··	1		·	2 · 2 =	2	4

.

Теперь можно вычислить D:

D =	−11	3	−	2	4	=	−13	−1
	−1	3		6	−8		−7	11

.

Определение. Квадратная матрица A порядка n называется обратимой, если существует такая матрица D порядка n что D · A = I. В этом случае матрица D называется обратной к матрице A. Матрица, обратная к матрице A обозначается A−1. Справедливы следующие утверждения.

Теорема. Если матрица A обратима, то обратима и матрица A−1 и (A−1)−1 = A. Теорема. Если матрица A обратима, то A−1 · A = A · A−1 = I.

Определители

Каждой квадратной матрице по определенному закону можно поставить в соответствии число, которое называется определителем этой матрицы.

Если A = (aij ) − матрица размерности n × n , то определитель этой матрицы обозначается либо DET A , либо

	a21		a22		. . . a2n
	a11		a12		· · ·	a1n
. . .					. . . .
	an		an		· · ·	ann
		1		2

Дадим определение определителя для матриц различной размерности.

def

1. Пусть A = (a11) − 1 × 1 , тогда DET A = a11 .

2. Пусть A = (aij ) − 2 × 2 , тогда

DET A =

a11

a12

def

· a22 − a12 · a21.

a21

a22

= a11

3. Пусть A = (aij ) − 3 × 3 , тогда

DET A =

a21

a22

a23

= (a11 · a22 · a33 + a12 · a23 · a31 + a13 · a21 · a32) −

a11

a12

a13

def

a

a

a

− (a13 ·

22

31

12 · a21

· a33

11

23

32

31

32

33

a · a + a

+ a · a · a ) .

Чтобы запомнить последнюю формулу можно воспользоваться правилом треугольников: слагаемые, заключенные в первую пару круглых скобок, получены путем перемножения элементов, стоящих на главной диагонали, (первое слагаемое), а текже перемножением элементов, стоящих в вершинах треугольников, основания которых параллельны главной диагонали (два других слагаемых). Аналогично получены слагаемые, заключенные во вторую пару круглых скобок: первое слагаемое - произведение элементов, стоящих на побочной диагонали, а два других слагаемых - произведение элементов, стоящих в вершинах треугольников, основания которых параллельны побочной диагонали.

На рисунке слева схематически указано правило вычисления первой группы слагаемых, а справа - второй группы слагаемых.

5

При некоторой тренировке вычисление определителя матрицы третьего порядка производится достаточно быстро.

Можно воспользоваться также правилом Саррюса (приписыванием двух первых столбцов), которое ясно из нижеследующего рисунка :

Определение. Пусть A = (aij ) - матрица размерности n × n . Минором Mij элемента aij (минором Mij соответствующим элементу aij ) называется определитель матрицы, полученной из матрицы A вычеркиванием i -ой строки и j -ого столбца. Алгебраическим дополнением Aij элемента aij (алгебраическим дополнением Aij соответствующим элементу aij ) называется величина (−1)i+j Mij , т.е.

Aij = (−1)i+j Mij .

Теперь дадим определение определителя для матрицы произвольной размерности n × n, где n ≥ 2:

		def		n
Определение.		DET A =		s=1 a1s · A1s .
(Эта формула	называется формулой вычисления определителя разложением по элементам 1-ой
			P

строки).

Легко показать, что это определение не противоречит предыдущим определениям.

Свойства определителей.

Далее строку или столбец будем называть ¾ряд¿.

1. При транспонировании, т.е. при замене каждой строки определителя столбцом с тем же номером,

определитель не меняется.
1	2		1		3
Пример. Пусть A = 3	4 , тогда AT =	2			4 . Легко проверить, что detA = detAT .
2. При перестановке двух строк или двух столбцов определитель лишь меняет знак.
Пример. Очевидны следующие равенства:			3		4		= −	4		3 ;		3		4	= −	1		2 .
				1	2				2	1			1	2			3	4

3.Если все элементы некоторого ряда равны нулю, то и определитель равен нулю.

4.Если элементы какого-либо ряда умножить на одно и то же число, то и определитель умножится

на это число.					3			4	=		3		4		=		3		4 · (−2) .
Пример. −2 ·
Обратите						1 2				1 · (−2) 2 · (−2)								1 2 · (−2)
матрицы
				внимание на следующее: при умножении матрицы на число надо все элементы этой
	умножить на данное число, если же умножаем определитель на число, то на это число
надо умножить элементы какого-либо одного ряда!
5. Если элементы двух параллельных рядов пропорциональны, то определитель равен нулю.
Пример.		7			14			= 7 · 1			7 · 2		= 7 · 1		2 = 0.
6. Если			1		2				1		2			1	2

каждый элемент k-ого ряда определителя представляет собой сумму двух слагаемых, то этот определитель может быть представлен в виде суммы двух определителей, первый из которых имеет в k-ом ряду первые из упомянутых слагаемых, а второй имеет в k-ом ряду вторые из упомянутых слагаемых, в остальных рядах эти определители имеют те же элементы, что и исходный определитель.

Пример. −15 =					3			4		=	3				4			=	3			4		+		3 4 = (4 − 6) + (−4 − 9) = −15.
7. Если						0 5					1 + (−1) 2 + 3									1 2						−1 3
	элементы какого-либо ряда умножить на одно и то же число и прибавить к соответствующим
					параллельного ряда, то определитель не изменится.
элементам другого
Пример. Легко проверить равенство															1	2					1		0
														3		4 = 3 −2 . Здесь второй определитель получен из перво-
		1 2						1 2 + 1 · (−2)							1			0
го умножением элементов первого												столбца на -2 и прибавлением к соответствующим элементам второго
столбца, т.е. 3			4		=		3			4 + 3 · (−2) =				3			−2 .

6

8. Сумма произведений элементов некоторого ряда на алгабраические дополнения этих элементов равна определителю. Т.е. справедливы равенства (в скобках приведено название этих формул):

DET A =

n

s=1 ais · Ais (вычисление определителя разложением по элементам i-ой строки).

P

n

DET A = Ps=1 asj · Asj (вычисление определителя разложением по элементам j-ого столбца).

Пример. Вычислим определитель некоторой матрицы разложением по элементам первой строки.

−3

9

6

= −2 · A11 + 4 · A12 + 3 · A13 = −2 · (−1)1+1 · M11 + 4 · (−1)1+2 · M12 + 3 · (−1)1+3 · M13 =

−2

4

3

−7

3

4

−2 ·

9

− 4 ·

−

3 6

+ 3 ·

3 9

= −2 · (36 − 18) − 4 · (−12 + 42) + 3 · (−9 + 63) =

=

3

−

−7 4

−7 3

= −36

6

162 =

6.

− 120 +

4

Таким же образом можно вычислять определители разложением по любому столбцу или по любой строке.

9. Сумма произведений элементов некоторого ряда на алгабраические дополнения соответствующих элементов другого параллельного ряда равна нулю.

n	n
Т.е. Ps=1 ais · Ajs = 0	, Ps=1 asj · Asi = 0	, если i 6= j .

Вычисление определителя получением нулей в какой-либо строке или каком-либо столбце.

Умножая элементы строк или столбцов на определенные множители, а затем складывая строки или столбцы, можно добиться того, что все элементы некоторого ряда, за исключением одного, будут равны нулю, а тогда вычисление исходного определителя сводится к вычислению одного определителя меньшего порядка. Таким образом, систематическое применение сначала седьмого свойства определителей, а затем восьмого свойства определителей позволяет свести вычисление определителя n-ого порядка к вычислению одного определителя (n − 1)-ого порядка, вычисление которого в свою очередь можно свести к вычислению определителя (n − 2)-ого порядка и т.д.

Договоримся о следующих обозначениях. Если элементы какого-либо ряда будем умножать на число, то это число будем записывать в круглых скобках напротив этого ряда, а стрелочкой, направленной к другому параллельному ряду, будем показывать к соответствующим элементам какого ряда будем

прибавлять полученные произведения.
				1			2		3				1	2	3 + 1 3				1	2		0	.
Примеры.				−2			3		−4		=		−2	3	−4 − 2 ·· 3		=		−2	3	−2
				3 −4					5				3 −4		5 + 3 · 3				3 −4 14
				(3)					↑
	1	2		3		(		2)						1			2			3		=		1	2	3	.
	−2	3		−4			−		=					−2			3			−4				−2	3	−4
	3 −4			5			←				3 + 1 · (−2) −4 + 2 · (−2) 5 − 3 · (−2)													1 −8 11

там 3-его столбца, а во втором - элементы 1-ой строки умножаем на -2 и прибавляем к соответствующим

В первом примере элементы 1-ого столбца умножаем на 3 и прибавляем к соответствующим элемен-

элементам 3-ей строки.

Из 7-го свойства определителей следует, что если элементы i-ого ряда умножить на одно и то же число и прибавить к соответствующим элементам j-ого параллельного ряда, затем элементы i-ого ряда умножить на одно и то же число и прибавить к соответствующим элементам k-ого параллельного ряда, то определитель не изменится (предполагаем, что числа i,j,k попарно не равны друг другу). Т.е. элементы какого-то выбранного ряда можно умножать на различные множители и прибавлять к соответствующим элементам других параллельных рядов, при этом величина определителя не изменится. Например, далее показано что элементы первого столбца умножили на 3 и прибавили к соответствующим элементам второго столбца, затем вновь элементы первого столбца умножили на 2 и прибавили к соответствующим элементам третьего столбца, после чего применили формулу вычисления опреде-

лителя разложением по элементам второй строки.									=
DET A =	−3	9	6		=	−3	9 − 3 · 3	6 − 3 · 2
	−2	4	3			−2	4 − 2 · 3	3 − 2 · 2
	−7	3	4			−7	3 − 7 · 3	4 − 7 · 2

(3)↑

(2)↑

7

=	−3	0	0		= −3 ·A21 + 0 ·A22 + 0 ·A23 = −3 ·(−1)2+1 · −18		−10	= 6.
	−2	−2	−1			−2	−1
	−7	−18	−10

Вычислим определитель этой же матрицы получением нулей во втором столбце и последующим

разложением по элементам этого столбца.

умножим элементы третьей строки на -1 и прибавим

−2

4

3

←

к соответствующим элементам

затем =

DET A =

−7 3 4

(−1) (−3)

первой

строки,

умножим элементы третьей строки на -3 и прибавим к

соответствующим элементам второй строки

5

1

−1

(−3)

теперь

умножим элементы

первой

5

1

−1

=

18

0

−6

=

строки на -3 и прибавим к соответ-! =

18

0

−6

=

−7

3

4

←

ствующим элементам третьей строки

−22

0

7

1+2

18

−6

=(применяем формулу вычисления определителя разложением по элементам второго столбца)=

= 1 · A12

+ 0 · A22 + 0 · A32

= (−1)

· M12 = −M12

= −

−22

7

= −(18 · 7 − (−22) · (−6)) = 6.

В общем случае алгоритм получения нулей в j-ом

столбце выглядит следующим образом: в j-ом

, т.е. a

=6 0.

столбце выбираем какой-нибудь элемент, который отличен от нуля.

Пусть это будет a

kj

kj

Тогда все элемнты строки, в которой находится выбранный элемент (в нашем случае это k-ая строка) умножаем на (−asj /akj ) и прибавляем к соответствующим элементам s-ой строки (s =6 k), в результате в s-ой строке в j-ом столбце получаем нуль. Аналогично выглядит алгорит получения нулей в строке.

Примеры. Вычислим определитель некоторой матрицы получением нулей в первом столбце и раз-

ложением по элементам этого столбца:

−3

= 2 · A11 + 0 · A21 + 0 · A31 = 2 · (−1)1+1 · M11 =

5

6

7

←

=

0 −3/2

2 3

4

(−5/2) (3/2)

2

3

4

−3 2 −5

←

0 13/2

1

=

2 ·

−3/2

−3

=

−3 −3

=

−3 + 39 = 36.

13/2

1

13 1

по

Теперь вычислим определитель этой же матрицы получением нулей во второй строке и разложением

элементам этой строки:

7 + 5 · (−7/5)

=

5

0

0 =

5

6

7

=

5 6 + 5 · (−6/5)

2

3

4

2 3 + 2 · (−6/5)

4 + 2 · (−7/5)

2 3/5

6/5

−3

2 −5

−3 2 − 3 · (−6/5) −5 − 3 · (−7/5)

−3 28/5 −4/5

(−6/5) ↑

(−7/5)

↑

28/5 −4/5

= 5 ·A21 + 0 ·A22 + 0 ·A23 = 5 ·(−1)2+1 ·

= −5(−12/25 −168/25) = 36.

3/5

6/5

Эти примеры показывают, что при

использовании вышеописанного алгоритма получения нулей в

строке или столбце (даже если все

элементы исходной матрицы были целыми числами) будет получена

матрица, некоторые элементы которой будут дробными числами. В случае когда элементы исходной матрицы целые числа можно изменить алгоритм получения нулей так чтобы иметь дело только с целыми числами. Пусть требуется получить нули в каком-либо ряде. Тогда сначала надо в этом ряде получить 1 или -1, а затем применить описанный выше алгоритм.

Пример. Вычислим определитель предыдущей матрицы получением нулей в первом столбце и разложением по элементам этого столбца, при этом все преобразования будем проводить так, чтобы иметь дело только с целыми числами. Для этого сначала получим, например, -1 в этом столбце:

	5	6	7		←	=	−1 −3 −5 .
	2	3	4	(−3)			2	3	4
	−3	2 −5					−3	2 −5
	Теперь
			получаем нули в первом столбце и применяем формулу вычисления определителя разложе-
нием по элементам этого столбца:									−3	−5	= 0 · A11 − 1 · A21 + 0 · A31 = −1 · (−1)2+1 · M21 =
	−1	−3	−5		(2)	(−3) =		−1
	2	3	4		←	←		0	−3	−6
	−3	2 −5						0 11 10

−3 −6

=	11	10	= −30 + 66 = 36.

8

Теорема об обратной матрице.

Справедливы следующие утверждения.

Теорема. Пусть A квадратная матрица порядка n . Для того, чтобы существовала обратная матрица A−1 необходимо и достаточно, чтобы DET A =6 0 .

Теорема. Пусть A квадратная матрица порядка n и DET A 6= 0 . Тогда

A−1 = 1		A12			A22		· · ·	An2
			A11		A21		· · ·	An1
	DET A		A	n .	A	n	· · ·	Ann
			1		2
			. . . . . . . . . .

.

Т.е. столбцами матрицы DET A ·A−1 являются алгебраические дополнения к элементам соответствующей строки матрицы A .

Покажем как вычисляется обратная матрица на следующем примере. Пусть

A =

2

1

2

. Тогда DET A = (−6 − 4 − 18) − (−4 − 9 − 12) = −3 6= 0, следовательно A−1

−3

−1

−2

−2

3

−3

существует. Находим алгебраические дополнения:

= −3, A12 = (−1)1+2M12 = −

= 5,

1

2

3

2

A11 = (−1)1+1M11

=

−3

−3

−2

−3

1+3

3

−1

2+1

1

−2

=

= 7,

= −

A13 = (−1) M13

−2

3

A21 = (−1) M21

−3

= −3,

3

2+2

=

−2

−2

= 2,

2+3

= −

−2 1

= 4,

A22 = (−1) M22

−2 −3

A23 = (−1) M23

−2 3

3+1

1

−2

3+2

−2 −2

=

= 0,

= −

= −2,

A31 = (−1) M31

−1

2

A32 = (−1) M32

3

2

A33 = (−1)3+3M33

=

−2

1

= −1.

Следовательно,

3

−1

A−1 = −3

−2 .

5

2

1

−3

−3

0

Действительно, A−1 · A = −3 ·

7

4

−1

=

5

2

−2

·

3

−1

2

1

−3

−3

0

−2

1

−2

7

4

−1

−3(−2) − 3 ·

= −3 ·

5(−2) + 2 · 3 − 2(−2)

−2

3

−3

5 · 1 + 2(−1) − 2 · 3

5(−2) + 2 · 2 − 2(−3) =

1

−3(−2) − 3 · 3 + 0(−2) −3 · 1 − 3(−1) + 0 · 3

2 + 0(−3)

−3

0

0

7 · 1 + 4(−1) − 1 · 3

7(−2) + 4 · 2 − 1(−3)

= −3 ·

7(−2) + 4 · 3 − 1(−2)

0 −3

0 = I .

1

0

0

−3

Ранг матрицы.

Пусть A = (aij ) - матрица размерности m × n. Выделим в этой матрице произвольные k строк и k столбцов. Элементы, стоящие на пересечении выделенных строк и столбцов образуют квадратную матрицу порядка k, определитель которой будем называть минором k-ого порядка. Очевидно, что матрица A обладает минорами любого пордка от 1 до наименьшего из чисел m и n. Если матрица A не является нулевой, то среди всех отличных от нуля миноров этой матрицы найдется хотя бы один, порядок которого будет наибольшим.

Определение. Рангом ненулевой матрицы называется наибольший из порядков отличных от нуля миноров данной матрицы. Ранг нулевой матрицы равен нулю по определению.

Ранг матрицы A обозначается через r(A). Очевидно, что выполнены неравенства 0 ≤ r(A) ≤ min(m, n).

9

Примеры. Пусть				A =	0	1	3	, так как	0	1
					2	0	1		2	0 = −2 =6 0, следовательно r(A) = 2.
Пусть B =	2	0	0	2					второго		порядка этой матрицы равны нулю, а, например,
	3	0	0	3 , так как все миноры

b11 = 2 6= 0, то есть имеется ненулевой минор первого порядка, следовательно r(B) = 1.

Системы линейных алгебраических уравнений

Система уравнений вида

a11 · x1 + a12 · x2 + ... + a1n · xn = d1

a21

1

22

2 ...

2n

n

2

(1)

· x

+ a

· x

· x

= d

am1 · x1 + am2 · x2 + ... + amn · xn = dm

называется системой m

линейных алгебраических уравнений с n неизвестными.

Если m < n, то система (1) называется недоопределенной.

Если m > n, то система (1) называется переопределенной.

Если d1 = d2 = ... = dm = 0 , то система (1) называется однородной.

Числа aij (i = 1; m, j = 1; n) называются коэффициентами системы (1), а матрица A = (aij ) - m × n называется основной матрицей системы (1).

a11

a12

· · ·

a1n

d1

−

am

am

· · ·

amn

dm

Матрицу A=

a21

a22

· · ·

a2n

d2

будем называть расширенной матрицей системы (1).

1

2

. . . . . . . . . . . . . . . . . . . . . . . . . .

d1

...

− m × 1

Числа di, i = 1; m называются свободными членами системы (1), а матрица D =

- матрицей свободных членов системы (1).

dm

x1, ..., xn - неизвестные.

Решить систему это значит найти все такие наборы чисел z1, ..., zn , подстановка которых во все уравнения системы вместо неизвестных x1, ..., xn превращает эти уравнения в верные равенства.

Система (1) может иметь единственное решение, бесчисленное множество решений и не иметь ни одного решения.

Однородная система уравнений всегда имеет хотя бы одно решение.

		x1
Если X =	xn			−n ×1 , то систему уравнений (1) можно записать в матричном виде следующим
	x2
		...
образом:
				A · X = D.	(2)

Таким образом уравнение (2) представляет собой матричную запись системы (1).

Теорема. (Теорема Кронекера-Капелли) Система линейных алгебраических уравнений имеет решение тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы.

Матричный способ решения системы

Пусть m = n и A−1 существует, тогда умножаем обе части равенства (2) слева на A−1 :

	A−1 · A · X = A−1 · D I · X = A−1 · D X = A−1 · D.
Полученная формула X = A−1 · D позволяет найти решение системы.
Пример. Решим следующую систему линейных алгебраических уравнений матричным методом
		6x1	+ 5x2	− 2x3	= 5,	(3)
		2x1	+ 6x2	− 5x3	= −20,
	−4x1		+ 2x2	+ 3x3	= −16.
Систему (3) запишем в	матричном виде:
			A · X = B,			(4)

10