SPD_Lektsii / СПД Лекция 4

Навчальна дисципліна	Системи передачі даних
Модуль 1	Завадостійке кодування
Змістовий модуль № 1	Коректувальні коди в однобічних системах передачі даних
Тема 3	Циклічні коди

Лекція № 4 Коди Боуза-Чоудхурі-Хоквінгема

ПЛАН ЛЕКЦІЇ

Навчальні питання:

1.Коди Боуза-Чоудхурі-Хоквінгема.

2.Кодування циклічних кодів БЧХ.

3.Декодування циклічних кодів БЧХ.

Навчально-матеріальне забезпечення:

1.ПЕОМ, мультимедійний проектор.

2.Презентація у форматі PowerPoint.

Навчальна література:

1. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: перевод с англ./ под ред.

Добрушина В.Л. – М.: «Мир», 1976 г. – 600 с.

1. Коди Боуза-Чоудхурі-Хоквінгема.

Коди Боуза-Чоудхурі-Хоквінгема (БЧХ) являють собою великий клас кодів, здатних виправляти кілька помилок. Вони займають помітне місце в теорії та практиці кодування. Інтерес до кодів БЧХ визначається щонайменше 3-ма наступними обставинами:

серед кодів БЧХ при невеликих довжинах ( n 511) існують гарні (але, як правило, не кращі з відомих) коди;

відомі відносно прості та конструктивні методи їхнього кодування та декодування;

повне розуміння побудови кодів БЧХ є найкращою відправною точкою для вивчення багатьох інших класів кодів.

Коди БЧХ незалежно відкрили Хоквингем (1959 р.) і Боуз і Рой-Чоудхури (1960 р.), що довели низку теорем, що встановлюють існування таких ЦК, у яких мінімізується число перевірочних символів, а також указують шлях пошуку утворюючих поліномів для цих кодів.

Коригувальні властивості ЦК можуть бути визначені на підставі наступної теореми: для будь-

яких значень m і tu існує ЦК довжиною n 2m 1, що виправляє всі помилки кратності tu і менш

( tu m ) і має не більш n k m tu перевірочних символів.
Метод побудови кодів БЧХ базується на тому, що утворюючий багаточлен G(x)		кодів БЧХ с
параметрами ( n, m ) і d БЧХ 2tu 1 визначається виразом:
G(x) НЗК 1(x), 3 (x), 5 (x), , БЧХ 2 (x) ,		(1)
де НЗК – найменше загальне кратне,	(x) – мінімальні багаточлени елементів і , тобто коренів
і
мінімального ступеня, dБЧХ – конструктивна мінімальна кодова відстань (для		кодів БЧХ
d БЧХ d0 ).

Як видно, основна задача при виборі того чи іншого ЦК, перш за все, зводиться до визначення утворюючого багаточлена G(x) , від вибору якого залежить корегувальна здатність

коду. Тобто, коди БЧХ будуються по заданій довжині кодового слова n і кратності помилок, що виправляються, при цьому кількість інформаційних розрядів k не відомо поки не обраний утворюючий поліном. Згідно з (1) утворюючі багаточлени можливих кодів БЧХ визначаються добутком мінімальних багаточленів з непарними індексами:

GБЧХ (x) 1(x), 3 (x), 5 (x), 7 (x), 11(x), 15 (x) .

Так, наприклад, при n 15, m 4 і різних tu число перевірочних символів буде дорівнює: tu 1, n k m tu 4 1 4 ; tu 2 , n k m tu 4 2 8 ; tu 3 , n k m tu 4 3 12.

Відповідні коди ( n, k ) будуть (15,11), (15,7), (15,3). Нагадаємо, що мінімальна кодова відстань dmin 2tu 1 і, стосовно, до ЦК вона частіше називається конструктивною відстанню. Якщо tu або величини dБЧХ вибрати занадто великими, то результуючий код буде тривіальним – у ньому

буде лише один r n або ні одного інформаційного символу.

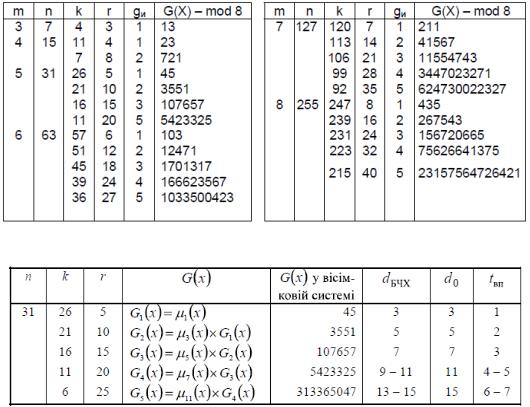
У табл. 1 і 2 дані параметри та утворюючі поліноми деяких кодів БЧХ. Коди БЧХ прийнято ділити на короткі ( n 127) і довгі ( n 127 ). Серед коротких кодів, код БЧХ (63, 39) з d0 =9 використовується також у системі ІНМАРСАТ. Поліноми приведені у восьмеричній формі запису, старший ступінь розташований ліворуч. Наприклад, коду (15, 7) відповідають двійковому

представленню 111010001 і багаточлен G(x) х8 х7 х6 х4 1 .

Коди БЧХ із довжиною 2m 1 називають примітивними кодами БЧХ. До них, зокрема, відносяться класичні коди Хемінга, що виправляють однократні помилки. До кодів БЧХ

відносяться також коди, довжина n яких є дільником 2m 1. Наприклад, код Голея (23, 12, 7) також

належить до класу кодів	БЧХ, оскільки при m 11 примітивний код БЧХ має		довжину n
n 2m 1 211 1 2047,	причому це значення без залишку ділиться на довжину коду Голея
n 23 (2047 : 23 = 89), що відноситься до непримітивних БЧХ-кодів.
На підставі даних табл. 1 можна побудувати графіки залежності швидкості передачі B k / n
від значення швидкості виправлення помилок v tu / n ,		що приведені в [1]. Якщо відношення
tu / n залишається постійним, то швидкість передачі B		прагне до нуля, коли n	необмежено
зростає.
			Таблиця 1
Параметри та утворюючі поліноми деяких кодів БЧХ

Таблиця 2

Параметри кодів БЧХ довжини 31

Як відзначалося вище, всі примітивні коди БЧХ мають конструктивну відстань d БЧХ 2tu 1. Мінімальну кодову відстань наведених в табл. 1 і 2 кодів можна збільшити,

вводячи при обчисленні G(x) мінімальний багаточлен 0 (x) x 1 ( G1(x) 0 (x) GБЧХ (x) ). Основою для побудови кодів БЧХ може слугувати табл. 2. Описана вище процедура дає

можливість отримати утворюючі багаточлени примітивних кодів довжиною n 2m 1, що мають зростаючий степінь G(x) і більш високу корегувальну здатність. Наприклад, щоб збільшити

відстань до 2tu 2 , потрібно основний утворюючий поліном БЧХ-коду помножити на біном x 1, тобто G1(x) (x 1) GБЧХ (x) , що спричинить за собою додаток до коду одного перевірочного

символу, який забезпечує перевірку на парність всіх символів БЧХ-коду. Таким чином, утворюється розширений БЧХ-код. Адекватно можна одержати укорочений (усічений) БЧХ-код відповідно до наступного алгоритму.

Укорочені циклічні коди. Оскільки ЦК породжуються дільниками бінома xn 1, то для більшої частини значень n і k мається відносно мало кодів, що задовольняють усім властивостям ЦК. Тому, природно спробувати знайти серед лінійних кодів такі, які хоча й не є в дійсності циклічними, володіють схожою математичною структурою та настільки ж легко реалізуються.

Укорочені ЦК одержують з повних ЦК, використовуючи для передачі інформації тільки КК повного коду, що містять ліворуч l нулів. Це дає можливість побудувати УЦК ( n l, k l ) шляхом

виключення перших l стовпців і l рядків з матриці, що породжує. Отриманий код не буде строго циклічним, тому що циклічний зсув не завжди буде приводити до одержання чергової дозволеної КК. Тому, укорочені (усічені) ЦК часто називають псевдоциклічними або квазициклічними. Укорочені ЦК зберігають основні властивості класичних ЦК, до числа яких відносяться наступні:

1. УЦК утворяться дільниками бінома xn 1 – утворюючими поліномами G(x) такими ж, як у повних ЦК;

2.УЦК відносяться до класу лінійних (групових) кодів, для яких сума дозволених кодових комбінацій УЦК також є дозволеною кодовою комбінацією;

3.УЦК володіє такою же мінімальним (конструктивним) кодовою відстанню як у вихідного ЦК, і таким же числом перевірочних символів, але не може бути щільно упакованим;

4.УЦК виправляє таке ж число помилок, що і ЦК;

5.при побудові кодеків УЦК використовуються ті ж схеми, що і для класичних ЦК, за умови, що кожному усіченому коду попереду приписується l нулів.

2. Кодування циклічних кодів БЧХ.

Більшість циклічних кодів використовують один алгоритм побудови завадостійких кодових комбінацій, а відрізняються лише методикою вибору утворюючого багаточлена. У БЧХ-коді побудова утворюючого багаточлена, в основному, залежить від двох параметрів: від довжини КК n і від числа помилок, що tu виправляються. Особливістю коду є те, що для виправлення числа

помилок tu 2 ще недостатньо умови, що між комбінаціями коду мінімальна кодова відстань

dmin 2tu 1. Необхідно також, щоб довжина коду n задовольняла умові:
n 2h 1,	(1)

де h – будь-яке ціле число.

При цьому n завжди буде непарним числом і приймати значення: 1, 3, 7, 15, 31, 63, 127 і т. ін., тобто не всі m можуть бути задані користувачем. Обрана за формулою (1) величина n визначає число контрольних символів r:

r h tu tu log2 (n 1) .

(2)

При рішенні задачі вибору припустимого числа інформаційних символів при заданих коригувальних властивостях зручно користатися таблицею, у якій приведені співвідношення коригувальних і інформаційних розрядів для БЧХ кодів.

Побудова утворюючого багаточлена G(x) виконується за допомогою мінімальних багаточленів (x) . Утворюючий багаточлен являє собою добуток непарних мінімальних

багаточленів і є їх найменшим загальним кратної (НЗК). Максимальний порядок мінімальних багаточленів:

p 2tu 1 .		(3)
Порядок багаточлена використовується при визначенні числа співмножників. Для побудови
G(x) використовуються тільки непарні багаточлени.	Наприклад,	при tu 6 ними будуть:
1(x), 3 (x), 5 (x), 7 (x), 9 (x), 11(x) . Старший з них	має порядок	p 2 6 1 11. Число їх

дорівнює 6, тобто дорівнює числу помилок, що виправляються. Число мінімальних багаточленів, що беруть участь у побудові утворюючого багаточлена:

V tu ,	(4)
а старший ступінь:
v h .	(5)

указує рядок у таблиці мінімальних багаточленів, з якої звичайно вибирається багаточлен для побудови G(x) . Для побудови утворюючого багаточлена використовуються тільки непарні

багаточлени ступеня v . Іноді, допускається використання багаточленів і меншого ступеня. Ступінь утворюючого багаточлена, отриманого в результаті перемножування обраних мінімальних багаточленів:

b r v tu h tu .	(6)
У загальному вигляді, G(x) НЗК 1(x), 3 (x), 5 (x), , БЧХ 2 (x) . Приклад:	Розглянемо

побудову циклічного коду довжиною в 15 розрядів, що виправляє одну або 2 помилки. Згідно (1),

n 2h 1, відкіля	h log (n 1) log 16 4 .		Число контрольних символів r, згідно (2),
	2	2
r tu log2 (n 1) 2 log2 16 2 4 8 .		Порядок старшого з мінімальних багаточленів, згідно (3)
p 2tu 1 2 2 1 3 . Кількість мінімальних			багаточленів, що беруть участь у побудові
утворюючого багаточлена, згідно (4),		V tu 2 ,	старший ступінь, згідно (5), v h 4 . Ступінь

утворюючого багаточлена, згідно (6), b k 8.

З таблиці мінімальних багаточленів вибираємо багаточлени ступеня v 4 , з них вибираємо два (V 2 ) мінімальних багаточлени, порядок старшого з який дорівнює 3 ( p 3 ), тобто

вибираємо мінімальні багаточлени p1 і p3 :

G(x) 1(x) 3 (x) 10011 11111 111010001 x8 x7 x6 x4 1 .

Число інформаційних розрядів n r 15 8 7 .

Перший рядок утворюючої матриці виходить шляхом додавання ліворуч від G(x) такого

числа нулів, щоб загальна довжина кодової комбінації був дорівнює n. Утворююча матриця виходить у результаті m кратного циклічного зсуву КК, що відповідає першому рядку утворюючої матриці:

000000111010001000001110100010000011101000100

С(15,7) 000111010001000 .001110100010000011101000100000111010001000000

Інші комбінації коду находять шляхом підсумовування всіких сполучень рядків утворюючої матриці. Таким чином, ми одержали набір КК для приведеного вище прикладу, що складає з 128 елементів.

На практиці, іноді потрібно закодувати в БЧХ-коді одну або кілька інформаційних посилок, для цього надходимо в такий спосіб:

1) вибираємо утворюючий багаточлен (методика вибору утворюючого багаточлена описана вище);

2)інформаційну комбінацію множимо на одночлен того ж ступеня, що й утворюючий багаточлен;

3)ділимо отриману комбінацію на утворюючий багаточлен;

4)підсумовуємо залишок від ділення з інформаційною комбінацією, помноженою на одночлен того ж ступеня, що й утворюючий багаточлен.

Наприклад, інформаційну комбінацію виду 1001101 закодувати в БЧХ-коді, так щоб код був здатний виправляти помилки кратності 2.

1. Інформаційна посилка 7-розрядна та коригувальні здібності коду рівні 2, отже, для цього випадку підходить багаточлен, обраний у попередньому прикладі.

2. Множимо 1001101 на x8 (100000000), маємо 1001101100000000 10011010000000.

3.Поділимо 100110100000000 на 111010001, у результаті ділення по модулю два, одержуємо залишок рівний 11000010.

4. Підсумовуємо:

10011010000000011000010 ,

100110111000010

100110111000010 – шукана комбінація. Причому, старших 7 розрядів інформаційні, а що залишилися 8 – контрольні.

Відзначимо наступні важливі властивості БЧХ-коду:

1. Максимальна кодова відстань dmax 2tu 1 1, таким чином, максимальна кодова відстань залежить від h.

2.Число інформаційних розрядів, що може бути використане при заданому числі h і максимальній кодовій відстані, виражається як ( h 1).

3.Декодування циклічних кодів БЧХ.

Виявлення і виправлення помилок відбувається по залишках від ділення прийнятої комбінації F (x) на утворюючий багаточлен G(x) . Якщо прийнята комбінація ділеться на

утворюючий багаточлен без залишку, то код прийнятий безпомилково. Залишок від розподілу свідчить про помилку, але не вказує, яку саме. Щоб знайти помилковий розряд і виправити його в циклічних кодах, прийнято здійснювати наступні процедури:

1)прийнята комбінація поділяється на утворюючий багаточлен;

2)підраховується кількість одиниць у залишку (вага залишку). Якщо W tu , де tu –

припустиме число помилок, що виправляються даним кодом, то прийнята комбінація складається по модулю 2 з отриманим залишком. Сума дасть виправлену комбінацію. Якщо W tu , то:

3) робимо циклічний зсув вліво прийнятої комбінації, поділяємо отриману в результаті циклічного зрушення комбінацію на утворюючий багаточлен G(x) . Якщо в залишку W tu , то

складаємо ділене з залишком. Потім робимо циклічний зсув вправо отриманої комбінації. Отримана комбінація вже не містить помилок. Якщо після першого циклічного зсуву та наступного ділення залишок виходить таким, що його вага W tu , то:

4)повторюється процедура п. 3) доти, поки не буде W tu . У цьому випадку,

5)виконується циклічний зсув вправо на стільки розрядів, на скількох була зсунута підсумована з останнім залишком комбінація щодо прийнятої комбінації. У результаті одержимо виправлену комбінацію.

Розглянемо процес виправлення помилок у БЧХ-коді (15,7). На приймальному кінці можуть бути прийняті наступні комбінації:

Варіант 1: Прийнятий комбінація: 111001100000100.

Крок 1. Ділимо прийняту комбінацію на утворюючий багаточлен:

.

Крок 2. Порівнюємо залишок з числом помилок, що здатний виправляти код. W 0 tu –

залишок дорівнює нулю, отже, прийнята комбінація не містить помилок. Варіант 2: Прийнята комбінація: 111001100010100.

.

W tu , отже,

.

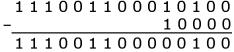Отримана після відповідного числа циклічних зрушень комбінація, не містить помилок

111001100000100.

Теоретично БЧХ-коди можуть виправляти довільна кількість помилок, однак з ростом кратності помилки значно зростає довжина коду, що неминуче веде до зменшення швидкості передачі та ускладненню приймально-передавальної апаратури.

Розробив:
доцент кафедри КІ
к.т.н., доцент	Слюсарь І.І.