SPD_Lektsii / СПД Лекция 5

Навчальна дисципліна		Системи передачі даних
Модуль 1		Завадостійке кодування
Змістовий модуль № 1		Коректувальні коди в однобічних системах передачі даних
Тема 4		Згорткові коди
Лекція № 5	Згорткові коди.

ПЛАН ЛЕКЦІЇ

Навчальні питання:

1.Синтез згорткових кодів.

2.Кодування з використанням ЗК.

3.Синдромне декодування ЗК.

4.Кодове дерево та решітчаста діаграма.

5.Алгоритм Вітербі.

6.Алгоритми пошуку по решітці.

Навчально-матеріальне забезпечення:

1.ПЕОМ, мультимедійний проектор.

2.Презентація у форматі PowerPoint.

Навчальна література:

1.Воробієнко П.П., Нікітюк Л.А., Резніченко П.І. Телекомунікаційні та інформаційні мережі: Підруч. для ВНЗ. – К.: Саммит-книга, 2010. – С. 62–94.

2.Олифер В.Г., Олифер H.A. Компьютерные сети. Принцип, технологии, протоколы: Учебник для вузов. 4-е изд. – СПб.: «Питер», 2010. – С. 118–156.

1. Синтез згорткових кодів.

У 1995 р. П. Елайєс запропонував згорткові коди (ЗК), які він розглядав як спосіб безперервної обробки інформації, а також довів застосування до них основної теореми Шенона. Того ж року радянським ученим Л.М. Фінком і В.І. Шляпоберським був уперше запропонований ЗК для виправлення пакетів помилок. Пізніше з’явилася більш докладна стаття Хегельбергера, що викликала появу інших робіт, присвячених ЗК для виправлення пакетів помилок. Хегельбергер увів назву «рекурентні коди» для кодів, в яких перевірочні символи на всій довжині кодової послідовності підпорядковуються тому самому рекурентному співвідношенню.

Одночасно з цим з’явилися статті, що описують виправлення незалежних помилок за допомогою ЗК. Особливо потрібно відзначити роботу Мессі, який запропонував для декодування ЗК простий та ефективний спосіб порогового декодування. У вищевказаних джерелах описуються методи декодування, засновані на використанні алгебраїчної структури кодів. Такі методи прийнято називати

алгебраїчними.

Паралельно розвивалося імовірнісне декодування ЗК, засноване на добірці кодової послідовності та перевірці правильності вибору за функцією правдоподібності. Стосовно до цієї групи послідовне декодування та деякі інші ймовірнісні алгоритми декодування ЗК виявилися єдиними способами декодування, що задовольняють умовам теореми Шенона.

Почнемо вивчення ЗК з опису способів їхнього подання. ЗК складніші для дослідження, ніж блокові коди. Для різних алгоритмів декодування зручно використовувати та різні способи подання ЗК. У зв’язку з тим, що ці способи призначені для опису тих самих кодів, доцільно навести співвідношення, що однозначно зв’язують всі способи подання між собою. Розглянемо приклад. На рис. 1 зображений кодер найпростішого ЗК. Символи xi,1 можуть набувати тільки

двох значень: 0 і 1. Кодер будемо вважати таким, що складається з таких основних елементів: розряду затримки (позначений прямокутником), і суматора mod2 ( ), що виконує операції за правилом: 0 1 1 і 1 1 0 .

Послідовність інформаційних символів xi,1 надходить на перший «контакт» (розряд)

вихідного розподілювача Р, а на другий розряд Р подається послідовність перевірочних символів xi,2 . У даному позначенні перший індекс відповідає номеру символу в послідовності, а 2-ий

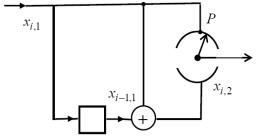
індекс – номеру самої послідовності. Вихідний розподілювач здійснює перемежування послідовностей, і в канал вони надходять у наступному вигляді: xi,1, xi,2 , xi 1,1, xi 1,2 , xi 2,2 , .

Послідовність символів з однаковим першим номером утворить «маленький» блок ЗК, ми будемо надалі називати його елементарним блоком (ЕБ). У кодері (див. рис. 1) інформаційні символи надходять у канал незмінними; такі коди та кодери за аналогією з блоковими називаються

систематичними. У наведеному прикладі перевірочні символи	xi,2 виражаються через
інформаційні за допомогою лінійного перевірочного співвідношення:
xi,2 xi,1 xi 1,1 ,	(1)

де самі символи складаються за модулем 2, а знак «–» в індексі має звичайне значення.

Рис. 1. Кодер найпростішого ЗК

Даний код дозволяє виправляти одиничні помилки, під якими ми будемо розуміти зміни значень переданих символів, що відбуваються на відносно великій відстані один від одного. Якщо рівняння (1) не виконується 2 рази підряд, то найбільш імовірно, що спотворено інформаційний символ xi,1 , оскільки рівняння (1) не виконується для xi,1 та xi 1,1, тобто для і-го і ( i 1)-го тактів часу. Якщо ж рівняння не виконується в і-му такті, а в ( i 1)-му та ( i 1)-му тактах виконується, то найімовірніше спотворений перевірочний символ xi,2 . Якщо ж спотворено два символи в

одному ЕБ або двох сусідніх ЕБ, то в наведеному коді неможливо зробити виправлення та потрібно застосовувати більш складні коди.

У лінійному систематичному блоковому коді розмірності ( n, k ) перевірочні символи блоку зв’язані n k перевірочними співвідношеннями з k інформаційними символами:

n k
xn k j	(ai, j xi ) для j 1,2, , n k ,	(2)
i 1
де xi – інформаційні символи, коли 1 i k ,	і перевірочні, якщо k 1 i n .
Основна ідея використання блокових кодів досить проста. Виберемо		множину з k

дискретних символів повідомлення, призначених для передачі, до них додаємо n k перевірочних символів, сформованих зазначеним способом, і передаємо символи всі разом у вигляді блока з п канальних символів. Якщо завади в каналі спотворюють малу частину цих п символів, то й n k перевірочних символів дають на приймальній стороні достатньо інформації, що дозволяє виявити або виправити помилки, які відбулися в каналі. У блокових кодах n k перевірочних символів будь-якого блока не пов’язані ніякою функціональною залежністю із символами сусідніх блоків.

ЗК також можна розділити на елементарні блоки (ЕБ) довжиною b , що складаються з кодових символів xi, j , (1,2, ,b ), де індекси позначають відповідно номер ЕБ у кодовій

послідовності та порядковий номер символу всередині ЕБ. ЗК використовується для перетворення інформаційної послідовності Z , що розбивається на ЕБ довжиною b k , тобто:

Z zi,1, zi,2 , , zi,b k , zi 1,1, zi 1,2 , , zi 1,b k , zi 2,1, zi 2,2 , , zi 2,b k .

Будемо вважати інформаційну послідовність Z , що складається з b k підпослідовностей

Z j , кожна з яких складається з символів zi, j , з однаковим 2-им індексом.
Більша частина матеріалу відноситься до двійкового поля, тобто	xi, j 0,1 . Будемо
відзначати щоразу окремо результати, що відносяться до поля Галуа GF (q)	або до розширеного

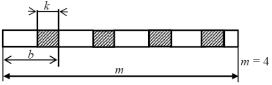
двійкового поля GF (21) . Надаємо спочатку визначення систематичного ЗК, на початку кожного

ЕБ якого є b k інформаційних символів, а в його кінці k перевірочних символів (рис. 2).

У зв’язку з введенням поняття елементарного блоку (ЕБ), при аналізі ЗК на відміну від блокових кодів, інформаційні елементи позначені символом k , а перевірочні m .

Рис. 2. Структура ЗК

Визначення 1. Систематичним згортковим b,b k К -кодом назвемо відображення множини

інформаційних послідовностей Z {zi, j } ( j 1,2, ,b k)						на множину кодових послідовностей
X {xi, j } ; послідовність X розділена на ЕБ довжиною b символів									( j 1,2, ,b) , містить у собі
незмінними символи інформаційної послідовності, тобто					xi, j* , для				( j* 1,2, ,b k ) , а символи
кожного з K сусідніх ЕБ	пов’язані між собою			за	допомогою				k	лінійних перевірочних
співвідношень:
			K 1 b	(a		x		) 0 ,
					j		i , j				(3)
			0 j 1	,
де 1,2, , m , коефіцієнти	a	, j	взяті з того ж поля,		що й символи					x	а знак означає
										i, j

підсумовування в цьому полі.

Число символів у К ЕБ, символи яких пов’язані перевірочними співвідношеннями (3),

називається кодовим обмеженням A :

A K b .

У виразі (3) не завжди можна в явному вигляді виразити перевірочні символи xi, j для b m 1 j b через інформаційні. Систематичні коди, в яких це здійснюване, тобто:

		K 1 b		(a	x
x	i,b m						) ,	(4)
		0 j 1		, j	i , j
будемо називати модульними.
Для b,b k К -ЗК, в яких є єдине значення			1 , будемо опускати індекс					у позначенні
коефіцієнтів. Якщо К 1 , то ЗК переходить у блоковий код,						для якого завжди можна подати

вираз (3) у вигляді (4), оскільки друге додавання відсутнє.

Таким чином, у систематичних ЗК інформаційні символи залишаються незмінними, а кожний з m перевірочних символів будь-якого ЕБ є лінійною функцією символів К сусіднього

ЕБ: даного й К 1 раніше переданих. У несистематичному ЗК всі b символів ЕБ є лінійними функціями сусідніх К b m символів інформаційної послідовності. Точне визначення

несистематичних ЗК подається нижче, а тут відзначимо лише, що вираз (3) справедливий і для них, однак, як буде показано нижче (3) однозначно визначає систематичний ЗК і не може однозначно визначити несистематичний код.

Приклад 1. Вираз (2) є перевірочним співвідношенням типу (4) для модульного 2,1 2 -коду. Приклад 2. 3,1 2 -код, що подається рівняннями:

xi,1 xi,3 xi 1,3 0 ( 1 )

xi,2 xi 1,1 xi 1,2 xi 1,3 0 ( 2 )

має наступні значення коефіцієнтів a , j :

a0(1,1) a0(1,3) a1(,13) a0(2,2) a1(,21) a1(,22) a1(,23) 1; a0(1,)2 a1(,11) a1(,12) a0(2,1) a0(2,3) 0

і не є модульним.

2. Кодування з використанням ЗК.

Основними характеристиками ЗК є величини:

k0 – розмір кадру інформаційних символів;

n0 – розмір кадру кодових символів;

m – довжина пам’яті коду;

k (m 1) k0 – інформаційна довжина слова;

n (m 1) n0 – кодова довжина блоку – це довжина кодової послідовності, на якій

зберігається вплив одного кадру інформаційних символів.

Нарешті, ЗК має ще один важливий параметр – швидкість R k / n , що характеризує ступінь надмірності коду, яка вводиться для забезпечення властивостей коду, що виправляють.

Як і блокові, ЗК можуть бути систематичними, несистематичними та позначаються як лінійні ЗК (n, k ) . Систематичним ЗК є такий код, для якого у вихідній послідовності кодових символів

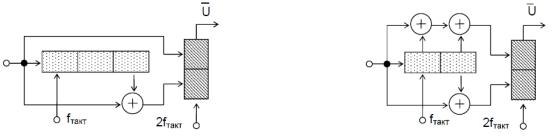
міститься без зміни його послідовність інформаційних символів, що породила. Інакше, ЗК є несистематичним. Приклади схем кодерів для систематичного (8,4) і несистематичного ЗК (6,3) приведені на рис. 3 і 4.

Рис. 3. Рис. 4.

Можливі різні способи опису ЗК, наприклад, за допомогою утворюючої матриці. Однак, у силу нескінченності КК і утворююча матриця буде мати нескінченні розміри. Точніше, вона буде складатися з нескінченного числа матриць G для звичайного блокового коду, розташованих уздовж головної діагоналі напівнескінченної матриці. Вся інша її частина заповнюється нулями. Однак, більш зручним способом опису ЗК є його завдання за допомогою імпульсної перехідної характеристики (ІПХ) еквівалентного фільтра або відповідного їй утворюючого полінома. ІПХ

фільтра (а кодер ЗК, по суті справи,	є фільтром) є реакція на одиничний вплив вигляду
(10000... Для кодерів, зображених на рис. 3 і 4, що відповідають ІПХ будуть мати вигляд:
	H a (11.00.00.01.00.00 ,	(5)
	Hb (11.10.11.00.00.00	(6)
Ще одна форма завдання ЗК –	це використання утворюючих	поліномів, однозначно
зв’язаних з ІПХ еквівалентного фільтра:

H	a	(x) 1 x x7	,	(7)
H	a	(x) 1 x x2	x4 x5 .	(8)
При цьому КК U на виході ЗК виходить у результаті згортки				вхідної інформаційної

послідовності т з ІПХ H . Розглянемо приклади кодування послідовностей з використанням ІПХ еквівалентного фільтра. Нехай m (111 , тоді для кодера з ИПХ H (11.00.00.01.00.00

або m (1011000

.

Іноді, зручніше розглядати повний утворюючий поліном ЗК G(x) як сукупність кількох

багаточленів менших ступенів, що відповідають коміркам вихідного регістра кодера. Так, для кодера рис. 5 відповідні часткові утворюючі поліноми будуть наступними:

G (x) 1 x x2			,	(9)
1
G	2	(x) 1 x2 .		(10)

Нехай, наприклад, кодується послідовність m (1010 . Відповідний інформаційний поліном запишеться як m(x) 1 x2 . Тоді, на вході першої комірки вихідного регістра при кодуванні буде

послідовність U (11011000 , який відповідає поліном U						1	(x) 1 x x3 x4 , а на вході другої
		1
комірки – U	2	(10001000 і,	відповідно, поліном U	2	(x) 1 x4 .			Легко помітити, що при цьому
справедливі рівності:
			U1(x) m(x) G1(x) ,					(11)
			U2 (x) m(x) G2 (x) .					(12)

Така форма запису зручна, оскільки видна структура кодера, (по набору поліномів можна відразу синтезувати пристрій). На практиці, поліноми задаються набором своїх коефіцієнтів. У табл. 1 приведені приклади кодерів ЗК, заданих своїми коефіцієнтами при ступенях утворюючих поліномів.

Таблиця 1

		G1		G2
		111		101
		1111		1101
		11101		10011
		111011		10100111
		110001		11111001
В якості прикладу кодера з		k0 1, можна		привести кодер ЗК (12,9) Вайнера-Еша з
параметрами: k0 3 , n0 4 , k 9 ,		n 12 , R 3/ 4	(рис. 6). Нехай, наприклад, m (100.000.000... .

Тоді кодове слово U (1001.0001.0001.0000...) . Видно, що це – систематичний код, у якому до 3-

ох інформаційних символів додається один перевірочний, залежний від значень інформаційних символів не тільки поточного кадру, але й двох попередніх кадрів. При цьому, вплив одного кадру інформаційних символів поширюється на 12 символів КК, тобто кодова довжина блоку для цього коду n 12 .

S r H e H .

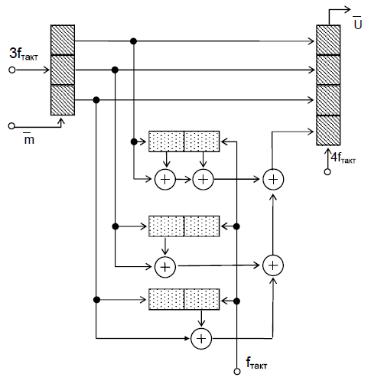
Рис. 6.

3. Синдромне декодування згорткових кодів.

Припустимо, що нами прийнята підлоги нескінченна послідовність м, що складається зі слова згорткового коду (ЗК) і вектору помилки:

r U e .

(13)

Аналогічно тому, як це робиться для блокових кодів, можна обчислити синдром прийнятої послідовності:

(14)

Однак через нескінченну довжину прийнятої послідовності (а ЗК являє собою безупинну нескінченну послідовність двійкових символів) синдром також буде мати нескінченну довжину і його пряме обчислення не має змісту.

Разом з тим можна помітити, що для розглянутих нами ЗК вплив одного інформаційного кадру поширюється усього на кілька кодових кадрів. Тому декодер може доглядати не весь синдром, а обчислювати його компоненти в міру надходження кадрів кодової послідовності, виправляти поточні помилки і скидати ті компоненти синдрому, що обчислені давно.

Для виправлення помилок при цьому декодер повинний містити таблицю сегментів синдромів і сегментів конфігурацій помилок, що утворять дані конфігурації синдрому. Якщо декодер знаходить у таблиці отриманий сегмент синдрому, він виправляє початковий сегмент кодового слова.

Схема декодера для ЗК Вайнера-Еша (12, 9) зображена нижче (рис. 7). Виправлення помилок за допомогою даного декодера виробляється на сегментах із 3-ох кодових кадрів – n 12 .

Декодер працює наступним чином. До вхідного регістру записується перший кадр прийнятої послідовності r (чотири символи). По першим трьох (інформаційним) символах кадру по тим же правилам, що й при кодуванні, визначається значення контрольного біта, що далі порівнюється з четвертим (перевірочним) символом прийнятого кадру.

При збігу контрольного та перевірочного бітів (а це буде, якщо помилки в першому кадрі немає) у першу комірку синдромного регістра записується 0, якщо ж у кадрі помилка є, – то 1. Далі, перший кадр прийнятої послідовності переноситься в регулюючий буфер, а до вхідного регістру заноситься черговий кадр прийнятої послідовності.

Після аналогічних перевірок для 2-го та 3-го кадрів прийнятої послідовності на виході

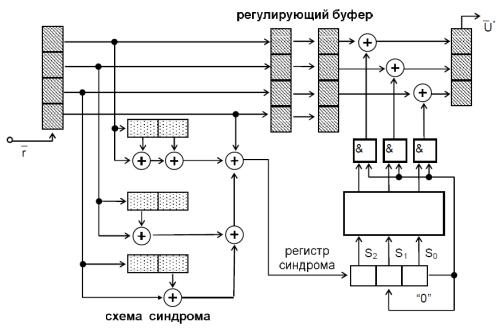
регулюючого буфера виявляється перший кадр прийнятої послідовності, у регістрі синдрому – 3- бітовий синдром, що відповідає прийнятому сегменту з трьох кадрів, а на виході адресної логіки – дешифрований по синдрому S вектор помилки e .

Виправлений кадр записується у вихідний регістр, при цьому виправлення виробляється тільки при наявності одиниці на входах схем «&», що відповідає присутності помилки саме в першому кадрі. Після виправлення помилки регістр синдрому скидається. Втрата 2-го та 3-го бітів синдрому при цьому не має значення, тому що ні в 2-му, ні в 3-му кадрах помилки бути не повинно (вона була в першому кадрі, а виходить, у фрагменті з 3-ох кадрів помилки більше бути не повинно). Всі можливі конфігурації помилок у перших 3-ох кадрах і відповідні їм перші 3 біти синдрому приведені в табл. 2.

Рис. 7. Декодер для ЗК Вайнера-Еша (12, 9)

Таблиця 2 Можливі конфігурації помилок у перших 3-ох кадрах і відповідні їм перші 3 біти синдрому

Конфігурація помилок у прийнятому сегменті				Синдром
1-й кадр	2-й кадр	3-й кадр	…	…
1000	0000	0000		111
0100	0000	0000		011
0010	0000	0000		101
0001	0000	0000		001
0000	1000	0000		110
0000	0100	0000		110
0000	0010	0000		010
0000	0001	0000		010
0000	0000	1000		100
0000	0000	0100		100
0000	0000	0010		100

4. Кодове дерево та решітчаста діаграма.

Ще одним дуже наочним способом опису та ілюстрації роботи ЗК є використання так званого кодового дерева. Розглянемо ЗК (6, 3) зі схемою, що наведена на рис. 8. Відповідне цьому кодеру кодове дерево – послідовність вихідних станів кодеру при подачі на його вхід ланцюжка вхідних символів 0 і 1 зображено на рис. 9. На даній діаграмі наведені вхідні та вихідні послідовності

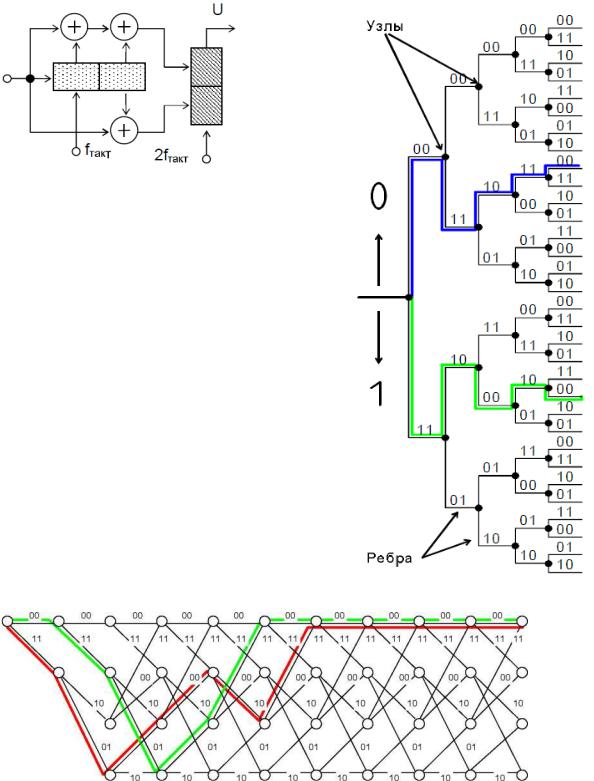
кодеру: вхідні – напрямком руху по дереву (нагору – 0, вниз – 1), вихідні – символами уздовж ребер дерева. При цьому кодування складається в русі вправо по кодовому дереву. Наприклад, вхідна

послідовність	m (01000	кодується	як	U (0011101100000 ,	послідовність
m (1010100000 – як U (1110001000 .

Рис. 8. Кодер ЗК (6,3)
Якщо уважно подивитися на побудову розглянутого
кодового дерева, можна помітити, що починаючи з 4-го
ребра його структура повторюється, тобто яким би ні був
перший крок, починаючи з 4-го ребра значення вихідних
символів кодеру повторюються. Однакові ж вузли можуть
бути об’єднані, і тоді починаючи з деякого перетину
розмір кодового дерева перестане збільшуватися.
Іншими словами, вихідна кодова послідовність у
визначений момент перестає залежати від значень
вхідних символів, введених у кодер раніше.
Дійсно, з рис. 3 видно, що, коли третій вхідний
символ вводиться в кодер, перший вхідний символ
залишає регістр зсуву та не зможе надалі робити впливу
на вихідні символи кодера. З врахуванням цього
необмежене кодове дерево, зображене на рис. 9,
переходить в обмежену ґратчасту діаграму (кодове дерево
з вузлами, що зливаються) рис. 10. Кодування ЗК з
використанням решітчастої діаграми, як і у випадку з
кодовим деревом, являє собою надзвичайно просту
процедуру: чергові символи вхідної послідовності
визначають напрямок руху з вузлів решітки: якщо 0, то
йдемо по верхньому ребру, якщо 1 – по нижньому ребру.	Рис. 9. Кодове дерево

Рис. 10.

Однак, на відміну від кодового дерева решітчаста діаграма не розростається по ширині з кожним кроком, а має починаючи з 3-го перетину постійну ширину.

Як приклад, закодуємо за допомогою решітчастої діаграми кілька інформаційних

послідовностей. Нехай	m (0110000 . Відповідна їй кодова послідовність		буде мати вид:
U (001101011100 ,	або m (110100 , тоді	U (1101010010110000 ; або	m (000000 ,
тоді U (1101010010110000 і т. ін.

5. Алгоритм Вітерби.

Найкращою схемою декодування коригувальних кодів, як уже відзначалося, є декодування методом максимальної правдоподібності, коли декодер визначає набір умовних імовірностей P(r /Ui ) , що відповідають усім можливим кодовим векторам Ui , і рішення приймає на користь

КК, що відповідає максимальному P(r /Ui ) .

Для двійкового симетричного каналу без пам’яті (каналу, у якому імовірності передачі 0 і 1, а також імовірності помилок виду 0 1 і 1 0 однакові, помилки в j ом і i ом символах коду

незалежні) декодер максимальної правдоподібності зводиться до декодеру мінімальної відстані Хемінга. Останній обчислює відстань Хемінга між прийнятою послідовністю r і всіма можливими кодовими векторами Ui ; і виносить рішення на користь того вектора, що виявляється ближче до

прийнятого. Природно, що в загальному випадку такий декодер виявляється дуже складним і при великих розмірах кодів n і k практично нереалізованим. Характерна структура ЗК (повторюваність структури за межами вікна довжиною n ) дозволяє створити цілком прийнятний по складності декодер максимальної правдоподібності.

Вперше ідея такого декодера була запропонована Вітербі. Працює він у такий спосіб. Припустимо, на вхід декодера надійшов сегмент послідовності r довжиною b , що перевищує кодову довжину блоку n . Назвемо b вікном декодування. Порівняємо всі кодові слова даного коду (у межах сегмента довжиною b ) із прийнятим словом і виберемо КК, найближчу до прийнятого. Перший інформаційний кадр обраної КК приймемо як оцінку інформаційного кадру декодованого слова. Після цього в декодер вводиться n0 нових символів, а введені раніше самі старі n0 символів

скидаються, і процес повторюється для визначення наступного інформаційного кадру.

Таким чином, декодер Витерби послідовно обробляє кадр за кадром, рухаючи по решітці, аналогічній, що використовується кодером. В кожен момент часу декодер не знає, у якому вузлі знаходиться кодер, і не намагається його декодувати. Замість цього декодер по прийнятій послідовності визначає найбільше правдоподібний шлях до кожного вузла та визначає відстань між кожним такої шляхом і прийнятою послідовністю. Ця відстань називається мірою розходження шляху. В якості оцінки прийнятої послідовності вибирається сегмент, що має найменшу міру розходження. Шлях з найменшою мірою розходження називається шляхом, що вижив.

Розглянемо роботу декодера Витерби на простому прикладі. Думаємо, що кодування виконується з використанням ЗК (6,3) (див. рис. 8), решітчаста діаграма, що відповідає цьому кодеру, наведена рис. 10).

Користуючись решітчастою діаграмою кодера, спробуємо, прийнявши деякий сегмент r , простежити найбільш ймовірний шлях кодера. При цьому для кожного перетину решітчастої діаграми будемо відзначати міру розходження шляху до кожного її вузла.

Припустимо, що передано кодову послідовність U (0000000 , а прийнята послідовність

має вигляд r 100010000 , тобто в 1-му та у 3-му кадрах КК виникли помилки. Як ми вже переконалися, процедура та результат декодування не залежать від переданої КК і визначаються тільки помилкою, що міститься в прийнятій послідовності. Тому, найпростіше вважати, що передано нульову послідовність, тобто U (0000000 . Прийнявши першу пару символів (10),

визначимо міру розходження для першого перетину решітки (див. рис. 10), прийнявши наступну пару символів (00), – для другого перетину і т. ін. При цьому з вхідних шляхів до кожного вузла залишаємо шлях з меншим розходженням, оскільки шлях з більшим на даний момент розходженням, вже не зможе стати надалі коротше.

Помітимо, що для розглянутого прикладу, починаючи з 4-го рівня, метрика (або міра

розходження) нульового шляху менше будь-якої іншої метрики. Оскільки помилок в каналі більше не було, ясно, що зрештою, як відповідь буде обраний саме цей шлях. З даного приклада також видно, що шляхи, що вижили, можуть досить довго відрізнятися один від одного.

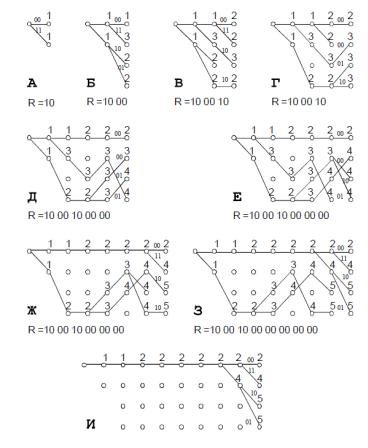
Однак, на 6-му – 7-му рівні перші 7 ребер всіх шляхів, що вижили, збіжаться один з одним. У цей момент відповідно до алгоритму Вітербі й приймається рішення про передані символи, тому що всі шляхи, що вижили, виходять з однієї вершини, тобто відповідають одному інформаційному символу. Процедура декодування послідовності з двома помилками ілюструється послідовністю, що наведена на рис. 11.

Рис. 11. Процедура декодування послідовності з двома помилками

Глибина, на якій відбувається злиття шляхів, що вижили, не може бути обчислена заздалегідь; вона є випадковою величиною, що залежить від кратності та імовірності виникаючих у каналі помилок. Тому на практиці звичайно не чекають злиття шляхів, а встановлюють фіксовану глибину декодування.

З рис. 5 видно, що вже на рівні Е ступінь розходження метрик правильного та неправильного шляхів досить велика ( dпр 2 , dош 4 ), тобто в даному випадку можна було б обмежити глибину

декодування величиною b 6. Однак, іноді більш довгий до даного перетину шлях може виявитися в остаточному підсумку самим коротким. Тому особливо захоплюватися зменшенням розміру вікна декодування b з метою спрощення роботи декодера не варто.

На практиці, глибину декодування звичайно вибирають у діапазоні n b n l , де l – число помилок, що виправляються даним кодом.

З рис. 11 видно також, що, незважаючи на наявність у прийнятому фрагменті двох помилок, його декодування відбулося без помилки і як відповідь буде прийнята передана нульова послідовність.