
Kontrolnaya_rabota_Matematika_v-t_3
.docx|
Автономная
некоммерческая организация высшего
профессионального образования «ПЕРМСКИЙ ИНСТИТУТ ЭКОНОМИКИ И ФИНАНСОВ» |
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Математика и статистика»
для студентов заочной формы обучения
Направление: 031600.62 Реклама и связи с общественностью
Вариант № 3
|
Выполнил: |
|
||
|
ФИО полностью (заполняется студентом) |
|||
|
Группа: |
|
||
|
(заполняется студентом) |
|||
|
Контактная информация: |
|
||
|
e-mail, номер сотового телефона (заполняется студентом) |
|||
|
Проверил: |
|
||
|
ФИО преподавателя |
|||
|
Дата: |
|
Оценка: |
|
|
Примечания: |
|
||
|
|
|||
|
|
|||
|
|
|||
Пермь 2013 г.
Задание № 1. Вычислить указанные пределы, не используя правило Лопиталя.
|
|
А) X0 = 3 |
Б) X0 = 1 |
В) X0 = |
Решение:
А)
При
 числитель
и знаменатель равны 0. Для раскрытия
неопределенности
числитель
и знаменатель равны 0. Для раскрытия
неопределенности
 разложим многочлены на произведение.
Корни уравнений являются делителями
свободных членов.
разложим многочлены на произведение.
Корни уравнений являются делителями
свободных членов.

Б)
При
 неопределенности
нет.
неопределенности
нет.
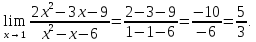
В)
При
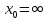 получается неопределенность
получается неопределенность
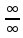 для ее устранения поделим числитель и
знаменатель на
для ее устранения поделим числитель и
знаменатель на
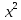 – старшую степень.
– старшую степень.
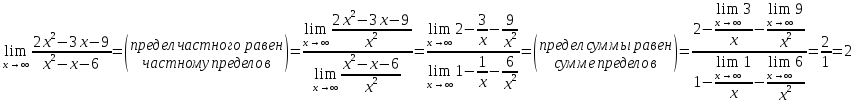
Задание № 2. Найти производные функций.
|
А)
|
Б)
|
Решение:
А)
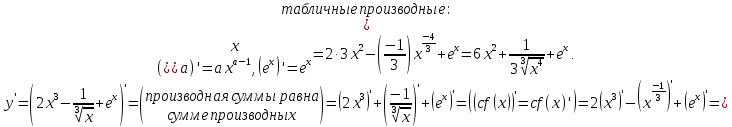
Б)
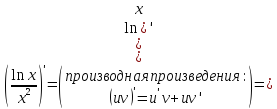
В)

Г)

Задание № 3. Для функции z=f(x,y) найти частные производные первого и второго порядков.

Решение:
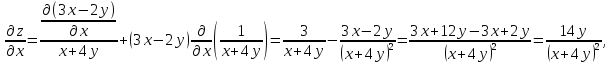
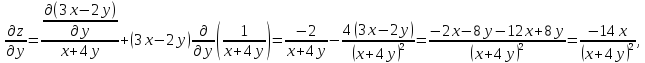

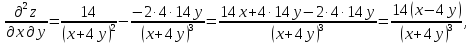
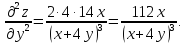
Задание № 4. Вычислить неопределенные интегралы.
|
А) |
Б) |
В) |
Решение:
А)

Воспользуемся
формулой интегрирования по частям
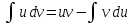 .
Положим
.
Положим
 .
Тогда
.
Тогда
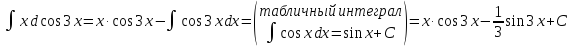
Исходный
интеграл
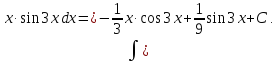
Б)
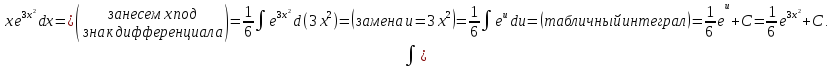
В)

Задание № 5.
Найти матрицу
С=3А-2В, где А= ,
В =
,
В =
 .
.
Решение:
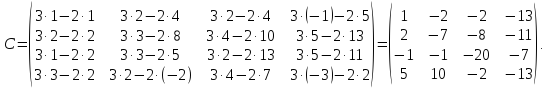
Задание
№ 6.
Вычислить
определитель матрицы А=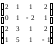 .
.
Решение:
Определителем
матрицы
 порядка
порядка
![]() называется число
называется число

где
![]() —
определитель квадратной матрицы порядка
—
определитель квадратной матрицы порядка
![]() ,
полученной из
,
полученной из
![]() вычеркиванием
первой строки и j-го столбца. Свойство:
если к
элементам некоторой строки (столбца)
матрицы прибавить соответствующие
элементы другой строки (столбца),
умноженные на произвольное число k,
то определитель полученной матрицы
будет равен определителю исходной
матрицы.
вычеркиванием
первой строки и j-го столбца. Свойство:
если к
элементам некоторой строки (столбца)
матрицы прибавить соответствующие
элементы другой строки (столбца),
умноженные на произвольное число k,
то определитель полученной матрицы
будет равен определителю исходной
матрицы.
Из
1-й строки вычтем 3-ю, тогда
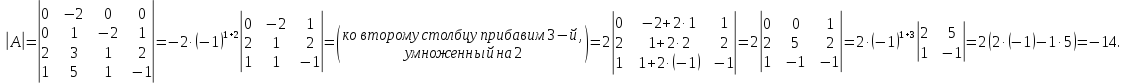
Задание
№ 7. Дана
матрица А=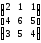 .
Найти Матрицу А-1
и установить, что АА-1=Е.
.
Найти Матрицу А-1
и установить, что АА-1=Е.
Решение:
Если
квадратная матрица
![]() является
невырожденной, то обратная для нее
существует и
является
невырожденной, то обратная для нее
существует и

Найдем
определитель
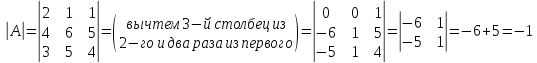 .
Тогда
.
Тогда
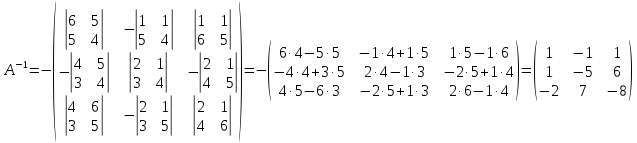
Проверим
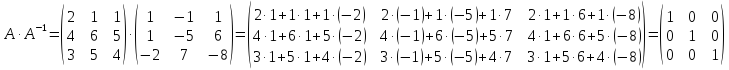
Задание
№ 8. Решить
систему линейных алгебраических
уравнений методом Крамера.
 .
.
Решение:
Пусть имеется система уравнений:
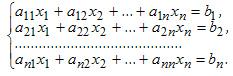
Обозначим через Δ определитель матрицы системы и через Δj определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы ( j=1,2,...n).
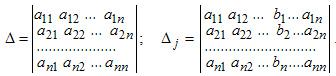
Если
определитель матрицы отличен от нуля,
т.е. Δ ≠0, то система имеет единственное
решение, которое находится по формуле:
![]()
Найдем
определители
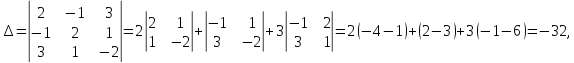
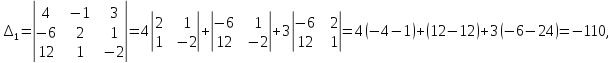
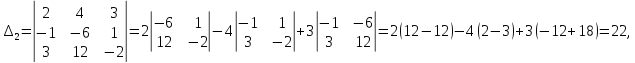
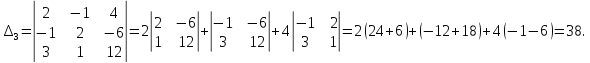
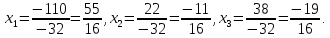
Задание № 9. Решить систему методом Гаусса даны элементы расширенных матриц систем 4-х уравнений с 4-мя неизвестными.
|
|
|
Решение:
Метод
Гаусса состоит в том, что совместную
систему n
линейных алгебраических уравнений
относительно n
неизвестных
![]() (определитель
матрицы системы отличен от нуля)
(определитель
матрицы системы отличен от нуля)

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
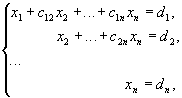
решение которой находят по рекуррентным формулам
![]()
А)
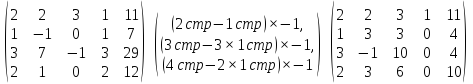



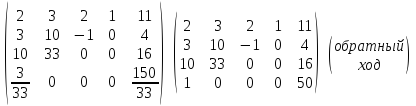
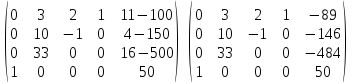

 .
.

Б)

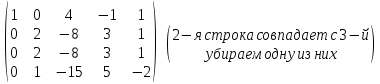

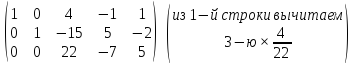
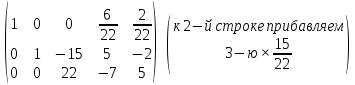
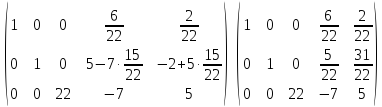
Система
имеет бесконечно много решений, ответ:

В)

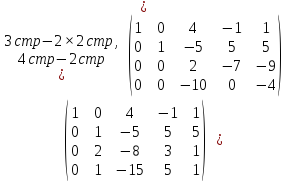


II часть контрольной работы
Задание № 10. Тема: Элементы комбинаторики: сочетания, размещения, перестановки.
Сколько разных требований на 3 книги может составить читатель, если в библиотеке 1000 наименований книг?
Решение:
Это
число есть по определению число сочетаний
по 3 из 1000:
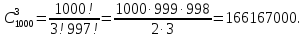
Задание № 11. Тема: Понятие случайного события. Классическое определение вероятности события.
Автомат, изготавливающий однотипные детали, даёт в среднем 6% брака. Из большой партии взята наудачу одна деталь для контроля. Найти вероятность того, что она бракованная.
Решение:
Найдем
вероятность выбора бракованной детали.
Согласно статистическому определению
вероятности частота выбора бракованной
детали вычисляется по формуле:
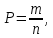
где
m — число выбора бракованной детали
в партии из n штук. В нашем случае
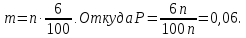
Задание № 12. Тема: Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей.
Из колоды в 36 карт вынимают 7 карт. Найти вероятность того, что среди них 4 дамы или 4 короля.
Решение:
Выбор
четырех дам и выбор четырех королей –
независимые события. Тогда по формуле
сложения вероятностей
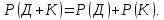 Очевидно, что
Очевидно, что
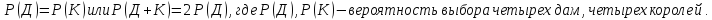 Найдем вероятность выбора четырех дам.
Количество благоприятных исходов равно
количеству способов выбора четырех дам
из семи карт, общее количество исходов
равно количеству выбора четырех дам из
тридцати шести карт. Тогда:
Найдем вероятность выбора четырех дам.
Количество благоприятных исходов равно
количеству способов выбора четырех дам
из семи карт, общее количество исходов
равно количеству выбора четырех дам из
тридцати шести карт. Тогда:

Искомая
вероятность равна
 .
.
Задание № 13. Тема: Формула полной вероятности. Формула Бейеса.
Вся продукция фабрики выпускается станками трех типов. На станках первого типа выпускается 30% всей продукции, на станках второго – 20%. Станки первого типа дают 2% брака, второго типа – 1,5% и третьего – 1,2%. Найти вероятность того, что наугад взятое изделие этой фабрики окажется бракованным.
Решение:
Рассмотрим гипотезы: Н1 – станок первого типа, Н2 – второго типа, Н3 – третьего типа. Их вероятности соответственно: Р(Н1) = 0,3; Р(Н2) = 0,2; Р(Н3) = 1-0,3-0,2 = 0,5. Событие А – наудачу взятое изделие бракованное. Условные вероятности:
Р(А/Н1) = 0.02; Р(А/Н2) = 0.015; Р(А/Н3) = 0.012
Полная вероятность:
Р(А) = Р(Н1)*Р(А/Н1) + Р(Н2)*Р(А/Н2) + Р(Н3)*Р(А/Н3) = 0,3*0.02 + 0,2*0.015 + 0,5*0.012 = 0,014.
Задание № 14. Тема: Формула Бернулли. Теорема Пуассона. Локальная и интегральные теоремы Лапласа.
В среднем 10% автомобилей, производимых заводом, имеют брак. Для контроля из партии автомобилей взяли 5 машин. Найти вероятность того, что среди них будет: а) 3 машины без брака; б) не более 3 машин без брака.
Решение:
Формула
Бернулли: Если вероятность p
наступления события Α
в каждом испытании постоянна, то
вероятность
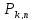 того, что событие A
наступит k
раз в n
независимых испытаниях, равна:
того, что событие A
наступит k
раз в n
независимых испытаниях, равна:
 ,
где
,
где
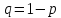 .
.
А)
Пусть p=0,9
вероятность того, что машина без брака.
По формуле вероятность того, что три
машины без брака равна:
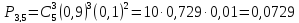 .
.
Б)
Найдем вероятность того, что без брака
будут 2,1,0 т.е.
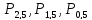 машин. Тогда искомая вероятность будет
равна:
машин. Тогда искомая вероятность будет
равна:
 .
.
Использованная литература
-
Баврин, И.И. Высшая математика: учебник для вузов / И.И. Баврин. - 7-е изд. - М.: Академия, 2008. - 616 с.
-
Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике : учеб. пособие для вузов / В. Е. Гмурман. - 11-е изд., перераб. - М. : Высшее образование, 2009. - 404 с.

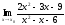
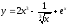 ;
В)
;
В)
 ;
; ;
Г)
;
Г)

 ;
;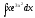 ;
;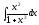 .
.