
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА-ЮГРЫ
«Сургутский государственный педагогический университет»
ФАКУЛЬТЕТ ФИЗИЧЕСКОЙ КУЛЬТУРЫ И СПОРТА
Реферат: «Поверхности второго порядка»
Работу выполнил: Картауз Д. гр.Б4011
Преподаватель: Демченко М.Л.
Сургут 2014г.
Содержание.
Понятие поверхности второго порядка. 1. Инварианты уравнения поверхности второго порядка.
Классификация поверхностей второго порядка.
Эллипсоид.
Однополостный гиперболоид.
Двуполостный гиперболоид.
Эллиптический параболоид.
Гиперболический параболоид.
Конус второго порядка.
Список литературы
1. Понятие поверхности второго порядка.
Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a11х2 + а22у2+a33z2+2a12xy+2a23уz + 2a13xz + 2а14 x + 2а24у+2а34z +а44 = 0(1)
в котором по крайней мере один из коэффициентов a11 , а22 , a33 , a12 , a23 , a13 отличен от нуля.
Уравнение (1) мы будем называть общим уравнением поверхности второго порядка.
Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение, полученное после преобразования координат, алгебраически эквивалентны.
Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение.

являются инвариантами уравнения (1) поверхности второго-порядка относительно преобразований декартовой системы координат.
.
2. Классификация поверхностей второго порядка
Эллипсоид.
Эллипсоидом
называется поверхность, которая в
некоторой прямоугольной системе
координат определяется уравнением:

(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
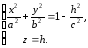 (2)
(2)
Исследуем уравнения (2) при различных значениях h.
Если
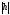 >c
(c>0),
то
>c
(c>0),
то
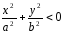 и уравнения (2) определяют мнимый эллипс,
т. е. точек пересечения плоскостиz=h
с
данным эллипсоидом не существует.
и уравнения (2) определяют мнимый эллипс,
т. е. точек пересечения плоскостиz=h
с
данным эллипсоидом не существует.Если
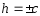 ,
то
,
то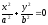 и линия (2) вырождается в точки (0; 0; +c)
и (0; 0; - c)
(плоскости
и линия (2) вырождается в точки (0; 0; +c)
и (0; 0; - c)
(плоскости
 касаются эллипсоида).
касаются эллипсоида).Если
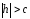 ,
то уравнения (2) можно представить в
виде
,
то уравнения (2) можно представить в
виде
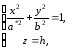
откуда
следует, что плоскость z=h
пересекает
эллипсоид по эллипсу с полуосями
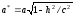 и
и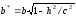 .
При уменьшении
.
При уменьшении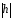 значения
значения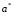 и
и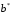 увеличиваются
и достигают своих наибольших значений
при
увеличиваются
и достигают своих наибольших значений
при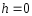 ,
т. е. в сечении эллипсоида координатной
плоскостьюOxy
получается
самый большой эллипс с полуосями
,
т. е. в сечении эллипсоида координатной
плоскостьюOxy
получается
самый большой эллипс с полуосями
 и
и .
.
Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.
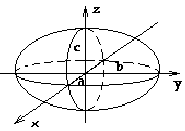
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.
2. Однополосный гиперболоид.
Однополосным
гиперболоидом называется поверхность,
которая в некоторой прямоугольной
системе координат определяется уравнением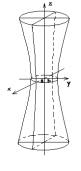
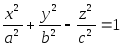 (3)
(3)
Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
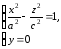 и
и 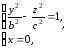
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
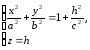 или
или 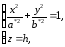 (4)
(4)
из
которых следует, что плоскость z=h
пересекает гиперболоид по эллипсу с
полуосями
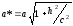 и
и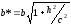 ,
,
достигающими
своих наименьших значений при h=0,
т.е. в сечении данного гиперболоида
координатной осью Oxy
получается самый маленький эллипс с
полуосями a*=a
и b*=b.
При бесконечном возрастании
 величиныa*
и b*
возрастают бесконечно.
величиныa*
и b*
возрастают бесконечно.
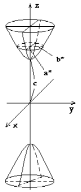
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
Величины a, b, c называются полуосями однополосного гиперболоида.
