Конспект Математическое моделирование. Автор: профессор МГОТУ Вилисов В.Я

ФИНАНСОВО-ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ

КАФЕДРА МАТЕМАТИКИ И ЕСТЕСТВЕННОНАУЧНЫХ ДИСЦИПЛИН

Вилисов В.Я.

Конспект лекций по курсу

«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»

Специальность 230700.68 "Прикладная информатика" Магистратура

Королев 2013

Вилисов В. Я. Математическое моделирование: Учебное пособие (конспект лекций) для магистратуры специальности 230700.68 (Прикладная информатика). - Королев: КИУЭС, 2013. - 42 с.

Рецензент: д. ф.- м. н., профессор Самаров К. Л.

Учебное пособие составлено в соответствии с требованиями Государственных образовательных стандартов высшего профессионального образования по специальности 230700.68 (Прикладная информатика) и Учебными планами ФТА.

Пособие представляет собой конспект лекций по четырем основным темам, изучаемых магистрами в курсе «Математическое моделирование». Содержание пособия соответствует программе курса, утвержденной УМС ФТА.

РЕКОМЕНДОВАНО Учебно-методическим		Программа рассмотрена и одобрена на
советом ФТА		заседании кафедры математики и
Протокол № от	2013 г.	естественнонаучных дисциплин.
		Протокол № от	2013 г.
Зав. кафедрой математики и		д. ф.- м. н., профессор Самаров К. Л.
естественнонаучных дисциплин

Компьютерная верстка:

© Финансово-технологическая академия, 2013 © Вилисов В. Я., 2013

Тираж экз. заказ № Отпечатано в типографии ФТА

г. Королев, ул. Гагарина д.42 тел.: [phone] www.kimes.ru, e-mail. :[e-mail]

Содержание
Введение: элементы моделирования................................................................................................	4
Термины ..........................................................................................................................................	4
Классификация моделей................................................................................................................	4
1. Задачи математического программирования (ЗМП) ..................................................................	5
1.1. Элементы ЗМП ........................................................................................................................	5
1.2. Прямая задача линейного программирования (ЗЛП) ..........................................................	6
1.3. Двойственная задача ЛП ........................................................................................................	7
1.4. Некоторые типовые прикладные задачи, представимые в форме ЗЛП.............................	9
1.4.1. Задача производственного типа......................................................................................	9
1.4.2. Задача о рационе (о составлении оптимальной смеси) ..............................................	10
1.4.3. Транспортная задача (или задача планирования перевозок) .....................................	11
1.5. Анализ чувствительности решения ЗЛП к изменению исходных данных .....................	13
1.5.1. Влияние коэффициентов ЦФ на решение ЗЛП ...........................................................	14
1.5.2. Влияние правых частей ограничений на решение ЗЛП .............................................	15
2. Многокритериальная оптимизация ............................................................................................	16
2.1. Скалярные и векторные критерии (показатели) ................................................................	16
2.2. Метод главного (доминирующего) критерия.....................................................................	16
2.3. Метод гарантирующего (максиминного) критерия...........................................................	17
2.4. Метод линейной (аддитивной) свертки ЦФ .......................................................................	17
2.5. Метод «идеальной точки»....................................................................................................	18
2.6. Метод последовательных уступок ......................................................................................	18
2.7. Метод, основанный на Парето-оптимальности .................................................................	18
3. Модели управления запасами .....................................................................................................	20
3.1. Задача управления запасами ................................................................................................	20
3.2. Процесс расходования и пополнения запасов....................................................................	21
3.3. Модель с постоянным спросом ...........................................................................................	22
3.4. Модель со скидками .............................................................................................................	23
3.5. Модель с дефицитом.............................................................................................................	25
3.6. Модель с производством (с постепенным пополнением запасов) ...................................	27
3.7. Многопродуктовая модель с ограниченным объемом склада..........................................	28
4. Методы и алгоритмы экспертного оценивания ........................................................................	30
4.1. Шкалы измерений .................................................................................................................	30
4.2. Ранжирование объектов .......................................................................................................	32
4.3. Парные сравнения .................................................................................................................	32
4.4. Обработка матрицы парных сравнений (один эксперт)....................................................	34
4.5. Обработка данных групповой экспертизы .........................................................................	36
4.6. Оценивание качества экспертов ..........................................................................................	39
Литература ........................................................................................................................................	42

3

Введение: элементы моделирования

Термины

Существуют три близких понятия, которые следует различать: задачи, модели и методы.

Задача – это конструкция, в которой есть исходные предпосылки и данные (дано), по которым следует найти решение (найти). Одну и ту же задачу можно решить разными методами.

Методы - это Способы или Алгоритмы выполнения операций над данными. Примеры методов: метод наименьших квадратов, метод скользящего среднего, метод экспоненциального сглаживания, …

Моделями называют некоторые копии, отражающие те или иные стороны объектов, субъектов или процессов.

В основе моделирования, т.е. построения моделей и их использования, лежит теория подобия.

При моделировании абсолютное подобие не достижимо, а поэтому необходимо лишь стремиться к тому, чтобы модель достаточно хорошо отображала необходимую сторону объекта, т.е. была адекватна объекту.

Один и тот же объект можно представить множеством моделей.

В некоторых случаях модель и задача могут использоваться как синонимы, а иногда и

метод.

Процедуры построения моделей впервые осознанно были использованы в период Второй мировой войны в Англии и послужили основой дисциплины Исследование операций

(ИО).

Классическая схема применения технологии и моделей ИО заключалась в следующих шагах:

1.Анализ объекта и определение цели исследования. Выбор учитываемых параметров, показателей качества и критериев.

2.Построение модели, адекватной объекту.

3.Исследование модели и поиск на модели оптимального решения для объекта.

4.Реализация решения и оценка его эффективности.

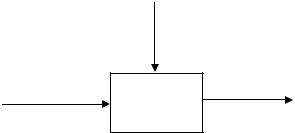
В математической модели объект представляется некоторым черным ящиком:

Параметры и структура объекта

Входные Объект Выходные параметры (модель) показатели

Классификация моделей

Основные признаки классификации моделей следующие (жирным выделены значения признаков, относящихся к математическим моделям).

1.По степени неопределѐнности:

Детерминированные

Стохастические

2.По степени отражения изменений во времени:

Статические

4

Динамические

3.По характеру учѐта временного фактора:

Дискретные

Непрерывные

Дискретно-непрерывные

4.По степени абстрагирования:

Виртуальные (от лат. virtus — потенциальный, возможный)

Реальные

5.Виртуальные могут быть представлены следующими группами: 5.1. Наглядные

Гипотетические

Аналоговые (аналоги)

Макеты

5.2.Символьные

Языковые

Знаковые

5.3.Математические

Аналитические (формульные)

Имитационные

Комбинированные

6.Реальные могут быть представлены следующими группами:

6.1.Натурные

Научный эксперимент

Производственный эксперимент

Комплексные испытания

6.2.Физические

В реальном масштабе времени (on-line)

В режиме разделения времени (off-line)

1.Задачи математического программирования (ЗМП)

1.1. Элементы ЗМП

- целевая функция V L(

) ,

1.

Первый элемент ЗМП

x

где вектор

переменных

[x

x

x

]T .

x

2

1

n

ЦФ связывает варьируемые переменные x с показателем качества V .

ЗМП функция V L(

)

В

x

может быть линейной или

нелинейной

относительно

переменных.

Целевая функция (ЦФ) отражает качество, моделируемого объекта.

Взависимости от смыслового содержания показателя V может возникать потребность

вего минимизации или максимизации за счет выбора наилучших значений переменных.

На основе ЦФ строится критерий.

Критерий – это правило выбора наилучших (оптимальных) значений переменных (аргументов), при которых показатель будет принимать своѐ экстремальное значение. Формально критерий записывается так:

V * L(x) max или min

x j			x j
или в другой форме:
x* arg max L(		)	или x* arg min L(		)
	x			x
x j			x j

Таким образом, первым элементом ЗМП является критерий.

5

2. Вторым элементом ЗМП являются ограничения, которые могут быть равенствами или неравенствами, линейными или нелинейными. В общем виде ограничения можно представить таким образом:

f (

)

или

f (

)

или

f (

)

x

a

x

a

x

a

ЗМП относятся к задачам условной оптимизации.

ЗМП часто называют моделями математического программирования (ММП) т.к. они отражают взаимосвязь независимых и зависимых переменных некоторого процесса, явления или объекта.

1.2. Прямая задача линейного программирования (ЗЛП)

ЗЛП относится к классу ЗМП. ЗЛП чаще других используется на практике. Особенность ЗЛП в том, что как ЦФ, так и функции ограничений линейны

относительно переменных.

n

L(

)

T

c j x j

max ,

x

c

x

j 1

x j

где

[c

c

c

]T - вектор параметров целевой функции;

c

2

n

1

[x

x

x

]T

- вектор переменных размерности n , на которые накладываются

x

2

n

1

следующие ограничения:

n

aij x j

ai0 ;

;

j 1

i 1, m;

j 1, n;

x j

0,

A

mn

- матрица коэффициентов системы ограничений;

aij

[a

a

a

]T - вектор свободных членов системы ограничений.

a

0

20

m0

10

Все ограничения формируют выпуклый многогранник, который называют областью допустимых решений (ОДР).

Пример (для двух переменных x1 и x2)

Дано (см. таблицу). На производстве ведется сборка двух видов изделий: И1, И2. При сборке могут быть использованы три группы операций: Оп1, Оп2, Оп3. Ежедневный фонд рабочего времени на каждую операцию составляет соответственно 430, 460 и 420 минут. Плановая прибыль на единицу каждого типа изделий составляет соответственно 3, и 2 у.е. Трудоѐмкость по операциям составляет соответственно: для И1 - 1, 3, 1 минут; для И2 - 2, 0, 4 минут.

			Таблица 1.2.
	Изделие 1	Изделие 2		Фонд рабочего
				времени, мин.
Операция 1, мин.	1	2		430
Операция 2, мин.	3	0		460
Операция 3, мин.	1	4		420
Прибыль, у.е.	3	2
Найти	x1	x2

Математическая постановка ЗЛП для 2-х переменных примет вид.

L(x) 3x1 2x2 max ,

x

6

x1 2x2				430
3x1 0x2				460 ,
x	4x		2	420
1
x j	0, j 1,2 .
Графическое решение ЗЛП .
500		Х2			2
400
300
200		1
100		3
0					2		31	Х1
		0		100	200	300	400	500

Оптимальное решение: x1=153.33 ; x2=66.67; L=593.33. L(x1; x2) имеет вид:

▲

	700 L
	600
	500
	400
	300
	200
	100								5 х2
									3
	0
	0	20	40	60	80	100			1
							120	140	160
	L=3*X1+2*X2								х1

1.3. Двойственная задача ЛП

Для прямой и двойственной задачи выполняется свойство симметрии, т.е. каждая из этой пары задач может быть прямой, тогда вторая будет ей двойственна.

Двойственная задача строится из прямой ЗЛП с помощью определенных правил:

1.Каждому из т ограничений прямой задачи соответствует переменная yi двойственной задачи, а каждой из п переменных xj прямой задачи соответствует ограничение двойственной задачи.

7

Коэффициенты целевой функции bi двойственной задачи равны коэффициентам правых частей ограничений ai0 прямой задачи и наоборот – правые части двойственной – это коэффициенты ЦФ прямой задачи.

2.Матрица коэффициентов левых частей ограничений двойственной задачи является транспонированной матрицей коэффициентов aij ограничений прямой задачи.

3.Критерию максимизации прямой задачи соответствует критерий минимизации двойственной задачи и наоборот.

4.Ограничения прямой задачи заменяются на ограничения в двойственной задачи.

Критерий оптимальности двойственной задачи примет вид:

m

y bi

W ( y)

b

T

yi

min ,

i 1

yi

b

]T

[a

a

]T - вектор параметров целевой функции

где

b

[b

b

a

20

m0

1

2

m

10

двойственной задачи т.е. вектор правых частей ограничений прямой задачи;

y [ y

y

2

y

m

]T - вектор переменных размерности m , на которые наложены

1

следующие ограничения:

m

aij

yi c j ;

i 1

;

i 1, m;

j 1, n;

yi 0,

A aij mn - матрица коэффициентов системы ограничений; в математической постановке двойственной задачи эта матрица используется в транспонированном виде:

AТ	a	ji	nm
								]T - вектор свободных членов системы ограничений двойственной
c [c				c	2	c	n
			1

задачи т.е. вектор коэффициентов целевой функции прямой задачи.

При решении ДЗЛП предполагаются известными A , c , a0 (т.е. b ), необходимо найти

оптимальный вектор y * .

В ОДР между ЦФ и критериями выполняется следующее отношение:

	n	m
max L(x) c j x j		bi yi	W ( y) min ,
x j	j 1	i 1	yi

В оптимальной точке выполняется строгое равенство.

Экономическая интерпретация прямой и двойственной задачи заключается в следующем.

Впрямой задаче целью является распределение ограниченных ресурсов для максимизации эффекта от продукции. При этом:

1.Целевая функция отражает выручку или прибыль по оптимальному количеству всех видов продукции x j , а c j - это прибыль на единицу продукции j-го вида.

2.Ограничения отражают допустимое к использованию количество т видов ресурсов, а ai0 - это их запасы.

Вдвойственной задаче целью является минимизация общей стоимости ресурсов (сырья или времени) при ограничениях на цену продукции. При этом:

1.Целевая функция отражает общую стоимость ресурсов, затраченных на производство. Коэффициенты ЦФ bi (т.е. ai0 ) – это количество ресурсов, а yi

можно трактовать как стоимость единицы ресурса i-го вида (т.е. его цена).

8

2. Ограничения		отражают границу роста себестоимости продукции. Разность
m
aij yi	c j	часто называют приведѐнными издержками.

i 1

Пример (продолжение).

Двойственная задача линейного программирования для предыдущего примера примет следующий вид:

W ( y) 430 y1 460 y2 420 y3 min ,

y

y1 3y2 y3 3 2 y1 0 y2 4 y3 2 ,

yi 0, i 1,3 .

Оптимальное решение, полученное с помощью симплекс-метода такое:

y1 1;

y2 2;

y3 0;

W 1350у.е.

Интерпретация результатов.

Если подставить оптимальное решение в ограничения, то лишь в 1-ом ограничении выполняется неравенство (7 >= 3), а это можно интерпретировать так, что цена продажи может быть увеличена до 7, т.е. имеется запас по цене 1-го изделия. Значения ЦФ обеих задач равны.

▲

1.4.Некоторые типовые прикладные задачи, представимые в форме ЗЛП

1.4.1.Задача производственного типа

Постановка задачи имеет вид, приведенный ранее:

				n
L(			) c j x j max ,
	x
				j 1				x j
	n
aij x j					ai0 ;				;
j 1
i 1, m;					j 1, n;

x j 0,

Особенности задачи:

распределяются ограниченные ресурсы (материальные, временные и др.);

спецификации (т.е. калькуляции) на производимую продукцию заданы. Они отражают количество материалов (комплектующих, ингредиентов, …), необходимое для производства единицы продукции каждого вида;

все коэффициенты левых и правых частей ограничений, а также коэффициенты ЦФ

неотрицательны: c j 0;

aij 0;

bi 0.

ЗЛП этого типа для случая 2-х переменных имеет такой вид:

9

x2

Оптимальное

решение

ОДР

x1

1.4.2. Задача о рационе (о составлении оптимальной смеси)

Этот тип задач по структуре напоминает Задачу производственного типа, но содержит дополнительные условия (ограничения).

Пример.

Дано. Предприятие производит пищевую добавку на основе смеси кукурузной и соевой муки в определѐнных пропорциях. Минимальная ежедневная потребность составляет 800 кг. Важными контролируемыми параметрами являются количество белка и клетчатки в смеси.

		Кукурузная мука	Соевая мука
	Белок (кг в 1 кг)	0.09	0.60
	Клетчатка (кг в 1 кг)	0.02	0.06
	Стоимость	0.30	0.90
	компонентов (руб/кг)

Дополнительные требования диетологов заключаются в том, чтобы в пищевой добавке было не менее 30% белка и не более 5 % клетчатки.

Найти рецептуру смеси минимальной стоимости.

Решение. Переменными будут количество кукурузной и соевой муки в ежедневном объѐме:

x1 – количество кукурузной муки в 1 кг смеси; x2 – количество соевой муки в 1 кг смеси. Тогда ЦФ и ограничения будут следующими:

L(x) 0.3x1 0.9x2 min ,

x

0.09x1 0.6x2 0.3(x1 x2 )

0.02x1 0.06x2 0.05(x1 x2 )

x1 x2 800

x j 0, j 1,2 .

Или после преобразований ограничения примут вид:

x1 x2 800
0.21x1 0.3x2			0 ,
0.03x	0.01x	2	0
1

Графическое решение этой задачи примет вид:

10