
Test_Matematika-1_3_3_Rus_2906
.pdf
Документ СМК |
Ф 10/6.163-2013 |
Тестовое задание
Редакция 3
Дата введения 01.09.2013
ТАРАЗСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ М.Х. ДУЛАТИ
Кафедра «Математика»
ТЕСТОВОЕ ЗАДАНИЕ
По дисциплине Математика-1 (3+3 кредита)
Для студентов 1 курса, специальностей
5В072400-Технологические машины и оборудование
5В071800-Электроэнергетика
5В070200-Автоматизация и управление
5В071900-Радиотехника, электроника и телекоммуникация 5В073100 - Безопасность жизнедеятельности и защита окружающей среды
1.Квадратная матрица называется диагональной, если….
A) все элементы вне главной диагонали равны нулю
B) все элементы побочной диагонали равны нулю С) все элементы главной диагонали равны нулю
D) все элементы матрицы равны нулю E) все элементы вне главной диагонали равны единице
2.Прямоугольная матрица A размеров m n называется квадратной, если …
A)m n
B)m n
С) m n
D)m n
E)m n
3. При умножении матрицы на число умножаются.
A)все элементы матрицы
B)все элементы какого-нибудь столбца С) все элементы какой-нибудь строки
D)все элементы побочной диагонали
E)все элементы главной диагонали
4.Умножение двух матриц определено только тогда, когда:
А) число столбцов первой матрицы равно числу строк второй матрицы В) число строк первой матрицы равно
числу столбцов второй матрицы С) число столбцов первой матрицы равно числу столбцов второй матрицы
D) числа строк и столбцов обеих матриц соответственно равны
E) число строк первой матрицы равно числу строк второй матрицы
5.Сложение двух матриц определено, если.
А) числа строк и столбцов обеих матриц соответственно равны В) число строк первой матрицы равно
числу столбцов второй матрицы С) число столбцов первой матрицы равно числу столбцов второй матрицы
D) число столбцов первой матрицы равно числу строк второй матрицы
E) число строк первой матрицы равно числу строк второй матрицы
6. Величина определителя равна нулю, если:

А) соответствующие элементы двух строк (столбцов) пропорциональны В) все элементы какой –либо строки
(столбца) умножить на число, не равное нулю С) переставить любые две строки
(столбца) определителя
D)строки определителя заменить столбцами
E)общий множитель элементов какойлибо строки (столбца) вынести за знак определителя
7 Величина определителя не изменится, если:
А) общий множитель элементов какойлибо строки (столбца) вынести за знак определителя В) все элементы какой –либо строки
(столбца) умножить на число, не равное нулю С) переставить любые две строки
(столбца) определителя
D)множитель какого-либо элемента строки (столбца) вынести за знак определителя
E)общий множитель элементов главной (побочной) диагонали вынести за знак определителя
8. Алгебраическое дополнение Àij элемента aij и минор M ij cвязаны соотношением:
А) Àij 1 i j M ij В) Аij 1 ij M ij С) M ij 1 ij Aij
D)Ai j M i j
E)A i j 1 i j i j
9. Определитель квадратной матрицы второго порядка вычисляется по формуле:
А) |
à11 |
à12 |
|
a a a a |
||||
|
|
à21 |
à22 |
|
11 |
22 |
12 |
21 |
|
|
|
|
|
|
|
||
|
à12 |
|
a a a a |
|||||
В) |
à11 |
|
||||||
|
à21 |
à22 |
|
11 |
22 |
12 |
21 |
|
|
|
|
|
|
|
|||
|
à12 |
|
a a a a |
|||||
C) |
à11 |
|
||||||
|
à21 |
à22 |
|
11 |
21 |
12 |
22 |
|
|
|
|
|
|
|
|||
D) |
à11 |
à12 |
|
a a a a |
||||
|
|
à21 |
à22 |
|
12 |
21 |
11 |
22 |
|
|
|
|
|
|
|
||
|
à12 |
|
a a a a |
|||||
E) |
à11 |
|
||||||
|
à21 |
à22 |
|
12 |
22 |
11 |
21 |
|
|
|
|
|
|
|
|||
10. Найти A12 в определителе четвертого
|
1 |
2 |
1 |
1 |
|
|
|
||||
порядка |
3 |
4 |
0 |
2 |
: |
5 |
5 |
0 |
0 |
||
|
2 |
1 |
1 |
1 |
|
|
|
|
|
|
|
A) 10
B) 10
C) 0
D) 1
E) 5
11. Решить уравнение
A)x 1, x 4
B)x 0
C)x 1, x 4
D)x 0, x 2
E)x 2
xx 1 0 :
4 x 1
12. Вычислить определитель квадратной
1 3 4
матрицы третьего порядка 0 2 3 :
1 2 1
А) 25
В) 20
С) 5
D)36
E)5
13. Вычислить определитель квадратной
1 2 3
матрицы третьего порядка 0 2 5 :
0 0 3
A) 6
В) 6
С) 24 D) 12

E) 12
14. Найти минор элемента a11
3 4 5
определителя 1 2 0 :
4 5 3
A)6
B)18
C)6
D)18
Е) 0
15. Найти алгебраическое дополнение
|
|
|
|
|
|
|
1 |
3 |
6 |
8 |
|
элемента a23 определителя |
1 |
1 |
5 |
3 |
: |
||||||
|
|
|
|
|
|
|
1 3 |
4 |
2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
1 |
|
А) |
36 |
|
|
|
|
|
|
|
|
|
|
В) |
130 |
|
|
|
|
|
|
|
|
|
|
С) |
18 |
|
|
|
|
|
|
|
|
|
|
D) 26 |
|
|
|
|
|
|
|
|
|
|
|
E) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. Пусть A |
0 |
3 |
4 |
|
. Вычислить |
|
|||||
|
|
2 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
определитель матрицы A :
A)1
B)0
C)2
D)1
E)3
17. Найти матрицу C A 2B , если
|
1 |
2 |
|
|
|
4 |
5 |
: |
|
A |
|
|
, |
|
B |
|
|
|
|
|
2 |
3 |
|
|
|
7 |
6 |
|
|
|
|
|
|
|
|
||||
|
7 |
8 |
|
|
|
|
|||
А) C |
|
9 |
|
|
|
|
|
||
|
12 |
|
|
|
|
|
|||
|
7 |
8 |
|
|
|
|
|
|
|
В) C |
|
|
|
|
|
|
|
|
|
|
16 |
9 |
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
С) C |
|
|
|
|
|
|
|
|
|
|
9 |
3 |
|
|
|
|
|
|
|
|
9 |
|
6 |
|
|
|
|
||
D) C |
14 |
|
|
|
|
|
|
||
|
|
17 |
|
|
|
|
|||
|
|
|
7 |
|
|
12 |
|
|
||
Е) |
C |
|
|
|
|
|
|
|
||
|
|
|
12 |
|
|
9 |
|
|
||
18. Найти произведение матриц A и B , |
|
|||||||||
|
|
|
|
1 |
|
3 |
4 |
|
||
если A |
|
2 |
|
|
||||||
|
|
, B |
: |
|
||||||
|
|
|
|
|
0 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
A) неперемножаются |
|
|
||||||||
B) |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
4 |
|
|
|
|
||||
C) |
|
6 |
8 |
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D) 1 |
1 |
|
2 |
|
|
|
|
|||
E) 0 |
|
|
|
|
|
|
|
|
|
|
19. Произведение матриц À 1 0 |
4 |
|||||||||
0
иB 3 , если эта операция возможна,
1
равно:
A)4
B)Указанная операция невозможна
C)0,0,0
4 D) 0
0 E) 0
20. Найдите произведение матриц A и B ,
|
|
2 |
1 |
, |
1 |
0 |
: |
|||
если A |
|
|
B |
3 |
4 |
|
||||
|
|
1 |
4 |
|
|
|
|
|
||
1 |
4 |
|
|
|
|
|
|
|
||
A) |
|
|
|
|
|
|
|
|
|
|
|
13 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
4 |
|
|
|
|
|
|
|
||
B) |
|
|
|
|
|
|
|
|
|
|
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
4 |
|
|
|
|
|
|
|
||
C) |
|
|
|
|
|
|
|
|
|
|
|
3 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
3 |
|
|
|
|
|
|
|
|
|
D) |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
|
|
|
|
||
E) |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21. Квадратная матрица A называется неособенной, если :
А) A 0
В) A 0
С) A 0
D) A 0
Е) A 0
22. Обратная матрица A 1 для квадратной матрицы 2-го порядка A находится по формуле:
A) |
A 1 |
|
1 |
|
|
A11 |
A21 |
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
A A12 |
A22 |
||||||
B) |
A 1 |
|
1 |
|
|
A11 |
A12 |
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
A A21 |
A22 |
||||||
C) |
A 1 |
A11 |
A21 |
|
||||||
|
A12 |
A22 |
|
|||||||
|
|
|
|
|
||||||
D) |
A 1 |
|
1 |
|
|
a11 |
a21 |
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
A a12 |
a22 |
||||||
Е) |
A 1 |
|
|
1 |
a11 |
a21 |
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
A a12 |
a22 |
||||
23. Найти обратную матрицу A 1 , если
|
1 |
2 |
|
||
A |
|
: |
|
||
|
|
|
|
|
|
|
4 |
9 |
|
||
А) |
|
9 |
4 |
||
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
||
В) |
1 |
9 |
|
||
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
||
С) |
|
9 |
2 |
||
|
|
|
|
|
|
|
|
4 |
1 |
|
|
|
|
|
|||
D) |
9 |
2 |
|
||
|
|
|
|
|
|
|
|
4 |
1 |
|
|
|
|
|
|
||
Е) 3 |
|
9 |
2 |
|
|
|
|
|
|
|
|
4 |
1 |
|
|
|
|
||
24. Для квадратной матрицы 2-го порядка
1 |
2 |
|
найти |
A 1 : |
|
A |
|
|
|
||
|
2 |
3 |
|
|
|
|
|
|
|
||
3 |
2 |
|
A) |
|
|
|
2 |
|
|
1 |
|
B) |
1 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
||
C) |
3 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
||
D) |
1 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
||
E) |
2 |
0 |
|
2 |
||
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
1 |
|
|
|||
25. Обратная матрица A 1 для квадратной матрицы 3-го порядка A находится по формуле:
|
|
|
|
|
|
|
A11 |
A21 |
A31 |
|||||
A) À |
1 |
|
1 |
|
|
A |
A |
A |
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
12 |
|
|
22 |
32 |
||
|
|
|
|
|
À |
A13 |
A23 |
|
|
|||||
|
|
|
|
|
|
|
|
A33 |
||||||
|
|
|
|
|
|
|
A11 |
A12 |
A13 |
|||||
B) À |
1 |
|
1 |
|
|
A |
A |
A |
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
21 |
|
|
22 |
23 |
||
|
|
|
|
À |
A31 |
A32 |
|
|
||||||
|
|
|
|
|
|
|
|
A33 |
||||||
|
|
|
|
A11 |
|
A21 |
|
|
A31 |
|
|
|||
C) À 1 |
|
A |
|
A |
|
|
A |
|
|
|||||
|
|
|
|
|
12 |
|
22 |
|
|
32 |
|
|
||
|
|
|
|
|
|
|
|
A23 |
|
|
|
|
|
|
|
|
|
|
A13 |
|
|
|
A33 |
|
|||||
|
|
|
|
|
|
|
a11 |
a21 |
a31 |
|
||||
D) À |
1 |
|
1 |
|
|
a |
a |
|
a |
|
||||
|
|
|
|
|
22 |
|
||||||||
|
|
|
|
|
|
|
|
12 |
|
|
32 |
|||
|
|
|
|
|
À |
|
|
a23 |
|
|
||||
|
|
|
|
|
|
|
a13 |
a33 |
||||||
|
|
|
|
|
|
|
a11 |
a12 |
a13 |
|
||||
Е) À |
1 |
|
1 |
|
|
a |
|
a |
|
|
a |
|
||
|
|
|
|
|
|
21 |
22 |
|
||||||
|
|
|
|
|
|
|
|
|
23 |
|||||
|
|
|
|
À |
|
|
a32 |
|
|
|||||
|
|
|
|
|
|
|
a31 |
a33 |
||||||
26. Система линейных алгебраических уравнений называется совместной, если она имеет:
А) хотя бы одно решение
B)бесконечное множество решений
C)число решений, равное числу неизвестных
D)число решений, равное числу уравнений Е) одно решение
27. Совместная система линейных алгебраических уравнений, если имеет только одно решение, называется:
А) Определенной B) Несовместной

C)Однородной
D)Неоднородной Е) Эквивалентной
28. Система линейных алгебраических уравнений всегда имеет решение, если. А) определитель системы отличен от нуля
B)определитель системы равен нулю
C)определитель системы имеет отрицательный знак
D)определитель системы равен единице Е) ранг матрицы системы равен трем
29. Решение СЛАУ из 3-х уравнений с 3 неизвестными x1, x2 , x3 находится по формулам Крамера:
А) |
x |
x |
|
|
, |
x |
x |
, |
|
x |
x |
|
|
|
||||||||||
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
A |
|
|
|
2 |
|
A |
|
|
|
3 |
A |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В) x |
A |
, |
x |
A |
|
, |
|
x |
A |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
1 |
|
x |
|
|
|
2 |
|
|
x |
|
|
|
3 |
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
С) x1 |
x |
, |
x2 |
x |
, x3 |
x |
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
||
D) |
x |
x |
|
, |
x |
x |
, |
|
x |
x |
|
|||||||||||||
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
A |
|
|
|
2 |
|
|
A |
|
|
3 |
|
A |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
E) x1 |
x |
|
A , |
|
x2 x |
|
A , |
x3 |
x |
A |
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|||
30. Решение матричного уравнения A X B , где A 0 определяется по формуле:
A)X A 1B
B)X BA 1 С) X ABA 1
D)X B 1 A
E)X AB 1
31. Элементарные преобразований системы линейных алгебраических уравнений применяют:
А) при решении СЛАУ методом Гаусса В) при решении СЛАУ по формулам Крамера С) при решении СЛАУ матричным методом
D) при вычислении определителя матрицы СЛАУ Е) при вычислении ранга матрицы СЛАУ
x 2 y z 2
32. Дана СЛАУ 2x 3y 2z 2 . Найти
3x y z 8
значение z из системы:
A)3
B)1
C)2
D)1
E)0
33. Найти значение y , решив СЛАУ
2x y z 1
x 2 y 3z 5 :x 3y 4z 6
A)1
B)1
C)2
D)2
E)3
34. Найти значение x , решив СЛАУ
x y 0
2 y z 1:z 2
A)x 12
B)x 0
C)x 32
D)x 3
E)x 1
35. Найти значение x1 , решив СЛАУ
x |
x |
|
2x |
2 |
|||
1 |
|
|
|
2 |
|
3 |
|
x2 |
2x3 |
3 |
: |
||||
x |
2 |
x |
0 |
|
|||
|
|
|
|
3 |
|
|
|
A)x1 3
B)x1 1
C)x1 5
D)x1 1
E)x1 9
36. Найти решение СЛАУ
x1 x3 1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x3 0 : |
|||||||||
x1 2x2 |
|
||||||||||||||||
x x |
2 |
0 |
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|||
A) |
|
; |
|
|
|
|
; |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|||
|
1 |
|
|
1 |
|
; |
3 |
|
|
|
|
||||||
B) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||
|
1 |
; |
1 |
|
|
3 |
|
|
|
|
|||||||
C) |
|
|
|
; |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|||
|
|
1 |
; |
1 |
; |
3 |
|
||||||||||
D) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
||||||
|
|
1 |
|
|
1 |
|
|
3 |
|
|
|
||||||
E) |
|
|
|
|
; |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
||||||
37. Найти значение x2 , решив СЛАУ
x1 x3 2
x1 x2 x3 6 :x2 3x3 5
A)x2 2
B)x2 2
C)x2 8
D)x2 1
E)x2 3
38. Найти значение x , решив СЛАУ
3x 4 y 11
5 y 6z 28 :x 2z 7
A) x 1 B) x 11 C) x 11 D) x 13 E) x 1
4x 5z 8 |
|
|
3 . Найти x |
39. Дана СЛАУ 2x y 2z |
|
|
|
x 3y 1 |
|
А) x 2
B)x 98
C)x 2
D)x 1 Е) x 49
40.Определитель, составленный из элементов, находящихся на пересечении выделенных k-строк и k-столбцов матрицы называется .
А) минором k-го порядка матрицы В) определителем матрицы С) базисным минором матрицы
D) алгебраическим дополнением элемента матрицы Е) минором элемента матрицы
41.Рангом матрицы называется:
А) наивысший порядок минора матрицы, отличного от нуля В) величина минора матрицы наивысшего порядка
С) порядок базисного минора матрицы D) число миноров матрицы наивысшего порядка Е) число всех миноров матрицы
42.Ранг матрицы не изменится, если: А) умножить элементы строк (столбца) матрицы на число отличное от нуля В) умножить элемент какой-либо строки
(столбца) матрицы на число отличное от нуля С) исключить строку (столбец) матрицы,
некоторые элементы которой равны нулю D) множитель какого-либо элемента строки (столбца) матрицы вынести за знак матрицы
E) умножить элементы главной диагонали матрицы на число отличное от нуля
43.Матрицы называются эквивалентными, если:
А) ранги матриц равны В) определители, порожденные этими матрицами равны
С) матрицы одинаковой размерности D) ранги матриц не равны
Е) матрицы разных размерностей
44.Для совместности неоднородной системы линейных алгебраических уравнений, необходимо и достаточно:
А) r( A) r(B)
B)A B
C)r( A) (B)
D)r( A) r(B)
Е) A B
45. Неоднородная система линейных алгебраических уравнений имеет единственное решение, если:
А) r( A) r(B) rc n
B)r( A) r(B) rc n
C)r( A) r(B) rc m
D)r( A) r(B)
Е) A B
46. Неоднородная система линейных алгебраических уравнений имеет бесконечное множество решений, если:
А) r( A) r(B) rc n
B)r( A) r(B) rc m
C)r( A) r(B) rc m
D)r( A) r(B) rc n
Е) A B
47. Неоднородная система линейных алгебраических уравнений несовместна, если:
А) r( A) r(B)
B)r( A) r(B) rc n
C)r( A) r(B) rc m
D)r( A) r(B)
Е) A B
48.Система линейных алгебраических уравнений, если имеет свободные члены равные нулю, называется:
А) Однородной B) Несовместной C) Определенной D) Неоднородной Е) Эквивалентной
49.Однородная система линейных алгебраических уравнений имеет нетривиальные решения, если:
А) r( A) n
B)r( A) m
C)r( A) m
D)r( A) n
Е) A 0
3 |
5 |
7 |
||
|
1 |
2 |
3 |
|
50. Найти ранг матрицы A |
|
|||
|
1 |
3 |
5 |
|
|
|
|||
А) r( A) 2 B) r( A) 3 C) r( A) 1 D) r( A) 0 Е) r( A) 9
51. Найти ранг матрицы
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B 0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
0 |
0 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) r(B) 2 |
|
|
|
|
|
|
|
|
|
|
B) r(B) 1 |
|
|
|
|
|
|
|
|
|
|
C) r(B) 5 |
|
|
|
|
|
|
|
|
|
|
D) r(B) 3 |
|
|
|
|
|
|
|
|
|
|
Е) r(B) 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
52. Найти ранг матрицы A |
2 |
3 |
1 |
6 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
2 |
6 |
||
|
|
|
|
|
|
|
|
|
|
|
А) r( A) 3 B) r( A) 4 C) r( A) 1 D) r( A) 0 Е) r( A) 18
53. Найти ранг расширенной матрицы
x y z 1 системы x y 2z 1
x y 3z 2
А) r(B) 3
B)r(B) 1
C)r(B) 5
D)r(B) 2 Е) r(B) 4

54. Найти ранг матрицы системы
x1 5x2 4x3 3x4 12x1 x2 2x3 x4 05x1 3x2 8x3 x4 1
А) r( A) 2
B)r( A) 4
C)r( A) 1
D)r( A) 0 Е) r( A) 3
55. Найти порядок базисного минора
x1 3x2 2x3 1
матрицы системы x1 9x2 6x3 3
x1 3x2 4x3 1
А) 2
B)нет базисного минора матрицы системы
C)1
D)0
Е) 3
56. Найти порядок базисного минора матрицы однородной системы
x1 3x2 2x3 02x1 x2 3x3 03x1 5x2 4x3 0
x1 17x2 4x3 0
А) 2
B)4
C)1
D)нет базисного минора матрицы системы
Е) 3
57. Найти ранг матрицы однородной
4x1 x2 10x3 0
системы x1 2x2 x3 0
2x1 3x2 4x3 0
А) r( A) 3
B)r( A) 2
C)r( A) 1
D)r( A) 44 Е) r( A) 3
58. Найти ранги матрицы и расширенной
x |
x |
x 4 |
||
|
1 |
2 |
3 |
|
|
|
2x2 3x3 |
0 |
|
матрицы системы x1 |
||||
|
|
|
|
|
2x |
2x |
16 |
||
|
|
1 |
3 |
|
А) r( A) 2 , r(B) 3 B) r( A) r(B) 2 C) r( A) r(B) 3 D) r( A) 1, r(B) 2 Е) r( A) 3 , r(B) 4
59. Система линейных алгебраических
x |
5x |
4x |
1 |
1 |
2 |
3 |
|
уравнений 2x1 10x2 8x3 3 является |
|||
3x 15x 12x 5 |
|||
|
1 |
2 |
3 |
системой А) несовместной
B)совместной и определенной
C)однородной
D)совместной и неопределенной Е) эквивалентной
63. Векторы, лежащие на одной прямой или на параллельных прямых называются. А) коллинеарными В) нулевыми
С) линейно-независимыми
D)противоположными
E)единичными
64.Векторы, расположенные в одной плоскости или параллельные одной и той же плоскости называются.
А) компланарными В) нулевыми
С) линейно-независимыми D) единичными
E) коллинеарными
65.Разложение вектора a по базису
i , j , k в пространстве имеет вид:
А) a axi ay j az k В) a axi ay j
С) a axi ay j az k
D)a i j k
E)a ax j ay k az i

66. Направляющие косинусы вектора a , заданного в пространстве находятся по формулам:
А) cos |
a |
x |
|
,cos |
|
|
ay |
|
|
|
,cos |
|
a |
z |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В) |
cos |
|
|
a |
|
|
|
|
,cos |
|
|
a |
|
|
|
|
,cos |
|
a |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
ax |
|
|
|
|
|
ay |
|
|
|
|
|
|
|
|
|
|
|
|
az |
|
|
|
|
|
|||||||||||||||||
С) |
cos ax ,cos ay ,cos az |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
D) cos |
a |
x |
|
,cos |
|
ay |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Е) |
cos |
|
a |
x |
|
|
,cos |
ay |
|
,cos |
|
a |
z |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 , a2 , a3 |
||||||||||
67. Угол между векторами a |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и b b1, b2 ,b3 |
|
определяется по формуле: |
|||||||||||||||||||||||||||||||||||||||||||||||
А) cos |
|
|
|
|
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
a |
|
|
|
2 a |
2 |
a |
z |
|
2 b 2 |
b 2 |
|
b |
2 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
z |
||||||||||
B) cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a |
x |
2 a |
2 |
a |
|
2 b 2 b 2 b 2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
z |
||||||||||
C) cos |
|
|
|
|
|
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
a |
x |
2 a |
2 |
a |
|
2 b 2 |
b |
2 |
b |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
z |
|||||||||||
D) sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
|
|
2 a |
2 |
a |
2 b 2 |
b |
2 |
b 2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
z |
|
|
|
|
|
||||||
Е) cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ax |
|
ay |
az |
|
|
|
|
bx by |
bz |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
68. Дан вектор a 3i 4 j 5k в виде
разложения по базису i , j , k . Укажите аппликату этого вектора:
A)5
B)3
C)4
D)3
E)6
69. Указать абсциссу единичного вектора для вектора a 3, 2, 1 :
A) |
3 |
|
||||
|
|
|
|
|||
|
|
|
|
|||
14 |
||||||
|
|
|||||
B) |
|
1 |
||||
|
|
|
|
|
||
14 |
|
|||||
|
|
|
||||
C)1
D)2
 6
6
E) 3
70 Дан вектор b (1;1; 0) . Косинус угла
между вектором b и осью OY равен:
A) 1

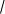 2
2
B) 0
C) 
 2
2
D) 1
E) 2 
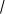 2
2
71.Найдите координаты вектора M1M 2 ,
если M1 (1;3), M 2 ( 5;6) : A) 6;3
B) 6;3 C) 4;9 D) 6;9 Е) 6; 3
72.Вычислить модуль вектора a(2;3; 6) :
A)7
B)11
C)5
D)3
E)1
73. Укажите координаты единичного
вектора BA0 , если известны координаты точек A 2, 3 и B 1, 2 :
|
3 |
|
|
|
|
|
1 |
|
|
|||||
A) |
|
|
|
|
|
|
, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||||
|
10 |
|
|
|
|
10 |
|
|
||||||
3 |
|
|
|
|
1 |
|
|
|||||||
B) |
|
|
|
|
|
, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||
|
10 |
|
|
|
|
10 |
|
|
||||||
3 |
|
|
1 |
|
|
|
|
|
|
|
||||
C) |
|
, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
4 |
|
|
|
|
|
|
|
||||
3 1
D),
1 2
E)3,1
74. Дан вектор a(1; 6;5) . Проекция вектора a на ось OX равна:

A)1
B)5
C)1
D)0
E)6
75. Найти вторую координату вектора a
|
|
|
2 |
|
|
|
если |
|
a |
13 и первая координата равна |
|||
6 -ти: |
|
|
|
|||
A) a1 (6; 4), |
a2 (6; 4) |
|||||
B) a1 |
(6; 2), a2 (6; 2) |
|||||
C) a1 |
(6;1), |
a2 (6; 1) |
||||
D) a1 (6; 2), |
a2 (6; 4) |
|||||
E) a1 (6;3), |
a2 (6; 3) |
|||||
76. Найти коэффициенты разложения вектора a(9;1) по векторам u(2;1) и
v (1; 0) :
A)a u 7v
B)a 7u 3v
C)a 7u v
D)a 7u v
E)a u 7v
77. Разложите вектор d 2; 3 по векторам a 1;0 и b 2; 3 :
A)d 4a b
B)a b d a b
C)d 3a 2b
D)d a 3b
E)d a b
78.Даны векторы a 2; 6 , b 1; . При
каком значении коэффициента векторы
a и b коллинеарны: А) 3 В) 3 С) 2
D) 2
Е) 4
|
|
1; 2;3 |
|
3; |
5; 4 . |
79. Даны векторы a |
и b |
||||
Определить координаты вектора |
|
|
|||
|
|
|
|
|
|
c 3 a |
5 b : |
|
|
|
|
А) c 18; 31; 29 В) c 4; 7;12 С) c 2;3; 1 D) c 20; 25;30 Е) c 4; 7;7
80. Даны длины векторов a 3, b 1 .
Угол между векторами равен 43 . Найти скалярное произведение векторов:
A) 3
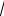 2 2
2 2
B) 3
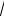 2 2
2 2
C) 
 2 2
2 2
D)3
 2
2
E)3
81 Даны векторы
a(1; 2; 2), b(2;3; 4), c(0;1; 2) . Укажите ортогональные векторы:
A)a и b
B)b и c
C)a и c
D)Ортогональных векторов нет
E)a, b , c
82. Найдите векторное произведение
векторов a i j k |
,b 3i 2 j 4k : |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) 2i j k |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B) 2i j k |
|
||||||||||||||
C) |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
29 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
D) |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
29 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E)
 6 2
6 2
83. Смешанное произведение векторов
a 4i j 3k; b 2i 3 j k; c i 5k :
A)60
B)54
