ЭВМ и ПУ. Лекция 02 1

Представление информации в ЭВМ. Кодирование информации. Арифметические основы ЭВМ.

1. Кодирование

Информация для целей ее машинного хранения и обработки всегда должна быть представлена в строго определенной форме. Любая внешняя форма, т. е. представление или изображение, информации может быть представлена конечной последовательностью знаков. Существует много различных систем представления, базирующихся на последовательностях знаков.

Поиски простых и экономичных представлений информации с помощью последовательностей знаков приводят к вопросам кодирования информации и кодам. Кодировка, или код, позволяют осуществлять переход от одной заданной системы представления рассматриваемой информации в виде знаков и последовательностей знаков к другому представлению той же информации также в виде знаков и их последовательностей.

При выборе способа кодировки в первую очередь учитываются две пели:

1.экономичность представления и обработки,

2.мера надежности от ошибок.

Из естественных соображений эффективности нас интересуют по возможности короткие кодовые слова с тем, чтобы представление информации в виде кодов было по возможности компактным, наглядным и более дешевым и обработка информации в выбранной системе представления должна быть простой и экономичной. С другой стороны, если в процессе передачи или обработки информации в кодовых словах появляются случайные незначительные ошибки, то нам, естественно, хотелось бы быть в состоянии такие "испорченные'' кодовые слова по меньшей мере выявлять и даже соответствующим образом их декодировать.

1.1. Коды и кодирование

Зададим конечное множество А знаков, которое называется также запасом знаков. Если это множество линейно упорядочено, то его будем называть также алфавитом. Особенно элементарным запасом знаков является множество В:

В = {1, 0}.

Элемент множества В называется двоичным знаком или битом (Bit – от

Binary Digit).

Множество конечных последовательностей знаков над запасом знаков А называется также множеством слов над А. При множестве В* = {1, 0}* мы

говорим о двоичных словах. Элементы множества Вn называются также n-битовыми словами или двоичными словами длины n. Множество n-битовых слов часто само снова используется в качестве запаса знаков.

1

Отображения между запасами знаков А и В, и в частности между словами над запасами знаков, называются кодами или кодировкой. Код есть

отображение с: А –> В

или, в случае кодировки целых слов, отображение с: А* –> В* .

Если запас знаков А состоит из отдельных литер, то мы говорим также о шифровке и множество образов называем шифрами.

В общем случае мы предполагаем, что кодировка является инъективным отображением: различные знаки и слова в этом случае отображаются на разные кодовые слова. Тем самым каждая кодировка

с: А –> В обратима на ее прообраз. Обратное отображение

d: {с(а): а А} –> А

для отображения кодировки с мы называем декодировкой или дешифровкой.

Тогда для всех знаков а А справедливо следующее: d(c(a)) = а.

Самой простой кодировкой является двоичная кодировка алфавитов. Это есть кодировки вида

с: А –> В*,

причем пусть А – заданный алфавит.

1.1.1. Коды постоянной длины

При двоичных кодировках, которые каждый кодируемый знак отображают на двоичное слово одинаковой длины, мы говорим о кодах постоянной дли-

ны. Таким кодировкам соответствуют отображения вида с: А –> Вn .

Поскольку часто из–за технических характеристик (как, например, длина регистров вычислительной машины) для представления кода имеется в распоряжении постоянное количество бит в настоящее время в информатике наиболее употребительны именно коды постоянной длины.

Пусть а, b – двоичные слова одинаковой длины; число позиций, в которых различаются слова а и b, назовем расстоянием Хэмминга. Расстоя-

нию Хэмминга математически соответствует отображение

Ham_dis: Вn х Вn –> N .

Значение этого отображения устанавливается следующим равенством

n1, если ai ≠ bi ,

Ham_dis (<a1...an>, <b1...bn>) = ∑di, где di =

i=1 0, иначе.

Большее расстояние кода допускает распознавание ошибок, а часто даже их исправление, однако при этом необходимы более длинные коды и тем с а- мым дополнительные затраты на представление и обработку. Это ведет к понятию избыточности кода.

Для алфавита А (т. е. для набора знаков А, на котором задан линейный (лексикографический) порядок) код постоянной длины называется кодом Грэя (или одношаговым кодом), если коды двух последовательных знаков из А раз-

2

личаются точно в одной позиции (в одном бите). В этом случае имеет место к о- дировка с расстоянием Хэмминга 1. >

Пример (4–битовый код Грэя для десятичных цифр). Четырехбитовый

код Грэя для десятичных цифр соответствует кодировке с: {0 9} –> B4.

Это отображение описывается табл. 1.1.

Zс(Z)

00000

10001

20011

30010

40110

50111

60101

70100

81100

91000

Таблица 1.1. Четырехбитовый код Грэя

Если в колах Грэя кодировки первого и последнего знаков отличаются тоже только в одной позиции (как в вышеприведенном примере), то говорят о

циклическом коде Грэя.

Применение лексикографического (линейного) порядка на двоичных словах непосредственно для кодирования линейно упорядоченного множества знаков приводит к формированию прямого кода.

Пример (прямой 4–битовый код для десятичных цифр). Определим кодо-

вое отображение с: {0 9} –> В4

с помощью табл. 1.2.

Zс(Z)

00000

10001

20010

30011

40100

50101

60110

70111

81000

91001

Таблица 1.2. Прямой 4–битовый код для десятичных цифр

1.1.2. Коды переменной длины

С кодами переменной длины технически труднее оперировать, чем с кодами постоянной длины. Из–за того, что в современных компьютерах исполь-

3

зуются слова определенной длины, такие коды в практике машинной обработки информации используются редко.

Пример (коды переменной длины).

(1)Код Морзе в двоичном кодировании Код Морзе строится из трех знаков, которые соответствуют “короткой",

"длинной" передаче (точки и тирс) и пробелу (“паузе”). Двоичная кодировка с: {., -, “пауза”} –> {01, 0111, 000} определяется следующим образом:

(2) Код для телефонных систем Телефонная система использует код для цифр диска набора номера. Та-

кой код, приведенный в табл. 1.5, порождается при наборе соответствующей цифры и передается в промежуточный узел.

Цифра Код

110

2110

31110

411110

5LLLLLO

6LLLLLLO

7LLLLLLLO

SLLLLLLLLO

9 LLLLLLLLLO

0LLLLLLLLLLO

Таблица 1.5. Код для телефонных систем

Коды переменной длины имеют одно важное преимущество. Если мы имеем данные о средней частоте появления знаков из А, то для часто встречающихся знаков можно выбрать короткие кодовые слова, а для редко встречающихся знаков – длинные, и тем самым получить небольшую среднюю длину кодовых слов.

Трудности использования кодов переменной длины становятся ясными, если учесть, что, вообще говоря, кодированию подлежат не только отдельные знаки, но и последовательности знаков. Если кодировка последовательности знаков производится конкатенацией кодов отдельных знаков, то при кодах переменной длины труднее распознать стыки знаковых кодов.

1.1.3. Последовательное и параллельное кодирование последовательностей знаков

Если мы хотим кодировать как отдельные знаки из А. так и слова над А закодированную информацию передавать по проводам, то – исходя из кодирования отдельных знаков из А – могут использоваться две принципиально различные возможности.

(1) Последовательная кодировка слов. Для заданной кодировки

4

с: А -> В*

отдельных знаков рассмотрим ее расширение на слова над А. Это значит, мы рассматриваем колировку с* нал А*, индуцированную колировкой с:

с*: А* -> В*

и определяемую следующим образом:

с*(ε) = ε

с*(<а1...an>) = c(a1)◦...◦с(аn).

Таким образом, при последовательной колировке слов мы кодируем слова w над А путем конкатенации кодов отдельных знаков слова w.

(2)Параллельная кодировка слов. Для заданной кодировки с с постоянной

длиной кодов с: А -> Вn

рассматриваем индуцированное отображение с':

с': А* -> (Вn)*

которое определяется следующими равенствами:

с' (ε) = ε

с'(<а1...an>) = c(a1)...с(аn).

Итак, при последовательной кодировке слов коды отдельных знаков подлежащего кодированию слова конкатенируются, в то время как при параллельном кодировании слов сохраняется структура кодируемого слова.

Пример (последовательное и параллельное кодирование слов). Табл. 1.2 показывает прямой код для десятичных цифр. Для последовательности цифр <2 5 3> при последовательном кодировании слова получаем кодировку

<001001010011>.

Для той же самой последовательности цифр <2 5 3> при параллельном кодировании слова получаем следующую последовательность двоичных слов:

<<0010> <0101> <0011L>>.

Более уместно параллельное кодирование представлять в следующем формате при векторном способе записи:

Вопрос кодирования слов особенно актуален при передаче кодируемой информации по проводам. При этом мы исходим из того, что по одному проводу в единицу времени (такт) может быть передан ровно один знак. В течение более длительного промежутка времени по одному проводу может быть передан не только код отдельного знака, но и последовательность знаков, представленная последовательностью кодовых слов. По аналогии с последовательным и параллельным кодированием слов говорят о последовательной и параллельной передаче.

Параллельная передача n–разрядного кода постоянной длины технически требует пучка из n отдельных проводов от отправителя к получателю. При этом за один такт передается целое слово. Последовательная передача требует толь-

5

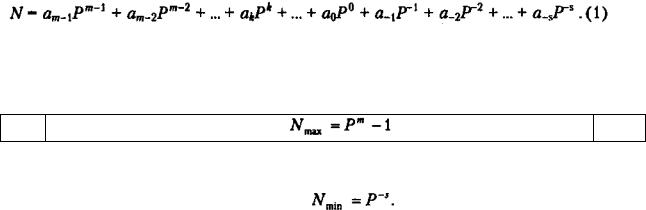
ко одного провода, но n тактов (отдельных шагов, на каждом из которых передается по одному биту) для передачи кодового слова длины n. Конечно, возможны и смешанные формы, как, например, при последовательной передаче групп двоичных слов по телеграфу.

Для последовательной передачи подходят и коды переменной длины, а для параллельной передачи годятся, вообще говоря, только коды с одинаковыми длинами кодовых слов. При отсутствии помех в параллельной передаче возможна тривиальная декодировка (если заданная функция кодирования по меньшей мере является инъективной). Однако это не имеет места для последовательной передачи.

Арифметические основы ЭВМ.

Информация в компьютере кодируется в двоичной или в двоичнодесятичной системах счисления.

Система счисления — способ именования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел системы счисления делятся:

□на позиционные;

□непозиционные.

Впозиционной системе счисления количественное значение каждой циф-

ры зависит от ее места (позиции) в числе. В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе.

Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до Р – 1. В общем случае запись любого смешанного числа в системе счисления с основанием Р будет представлять собой ряд вида

Нижние индексы определяют местоположение цифры в числе (разряд):

□положительные значения индексов — для целой части числа (m разрядов);

□отрицательные значения — для дробной части числа (s разрядов). Максимальное целое число, которое может быть представлено в m разрядах,

(2)

Минимальное значащее, не равное 0 число, которое можно записать в s разрядах дробной части,

Имея в целой части числа m, а в дробной — s разрядов, можно записать

всего Pm+s разных чисел.

Р = 2 и использует для

6

Существуют правила перевода чисел из одной системы счисления в дру-

Практически перевод из двоичной системы в десятичную можно легко выполнить, надписав над каждым разрядом соответствующий ему вес и сложив затем произведения значений соответствующих цифр на их веса.

Двоичное число 010000012 равно 6510. Действительно, 64 • 1 + 1 ■ 1 = 65.

Таким образом, для перевода числа из позиционной системы счисления с любым основанием в десятичную систему счисления можно воспользоваться выражением (1). Обратный перевод из десятичной системы счисления в систему счисления с другим основанием непосредственно по формуле (1) для человека весьма затруднителен, поскольку все арифметические действия, предусмотренные этой формулой, следует выполнять в той системе счисления, в которую число переводится. Обратный перевод выполняется значительно проще,

если предварительно преобразовать отдельно целую Nцел и дробную Nдр части выражения (1) к виду

Алгоритм перевода числа из десятичной системы счисления в систему счисления с основанием Р, основанный на этих выражениях, позволяет оперировать с числами в той системе счисления, из которой число переводится, и может быть сформулирован следующим образом:

1.При переводе смешанного числа следует переводить его целую и дробную части отдельно.

2.Для перевода целой части числа ее, а затем целые части получающихся частных от деления следует последовательно делить на основание Р до тех пор, пока очередная целая часть частного не окажется равной 0. Остатки от деления, записанные последовательно справа налево, образуют целую часть числа в системе счисления с основанием Р.

3.Для перевода дробной части числа ее, а затем дробные части получающихся произведений следует последовательно умножать на основание Р до тех пор, пока очередная дробная часть произведения не окажется равной 0 или не будет достигнута нужная точность дроби. Целые части произведений, записанные после запятой последовательно слева направо, образуют дробную часть числа в системе счисления с основанием Р.

Рассмотрим перевод смешанного числа из десятичной в двоичную систему счисления на примере числа 46,625. Переводим целую часть числа: 46/2 = 23 (остаток 0). 23/2 = 11 (остаток 1). 11/2 = 5 (остаток 1); 5/2 = 2 (остаток 1); 2/2 = 1 (остаток 0); 1/2 = 0 (остаток 1). Записываем остатки последовательно справа

7

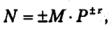
налево — 101110, то есть 4610 = 1011102. Переводим дробную часть числа: 0,625•2 = 1,250; 0,250•2 = 0,500; 0,500•2 = 1,000. Записываем целые части полу-

чающихся произведений после запятой последовательно слева направо —

0,101, то есть: 0,62510 = 0,1012. Окончательно 46,62510 =101110,1012.

Представление чисел с фиксированной и плавающей запятой

Ввычислительных машинах применяются две формы представления двоичных чисел:

□естественная форма или форма с фиксированной запятой (точкой);

□нормальная форма или форма с плавающей запятой (точкой).

Вформе представления с фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел по-

ложением запятой, отделяющей целую часть от дробной.

Например: в десятичной системе счисления имеется 5 разрядов в целой части числа (до запятой) и 5 разрядов в дробной части числа (после запятой); числа, записанные в такую разрядную сетку, имеют вид:

+00721,35500; +00000,000328; –10301,20260.

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях.

Диапазон значащих чисел N в системе счисления с основанием Р при наличии m разрядов в целой и s разрядов в дробной части числа (без учета знака числа) будет таким:

P-s < N < Рm – P-s.

Например, при Р = 2, m = 10 и s = 6 числа изменяются в диапазоне

0,015 < N < 1024.

Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение разрядной сетки и дальнейшие вычисления потеряют смысл. В с овременных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.

В форме представления с плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая — порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок – целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

где М — мантисса числа (|М | < 1); r — порядок числа (целое число); Р — основание системы счисления.

Например, приведенные ранее числа в нормальной форме запишутся так: +0,721355•103; +0,328•10-3; –0,103012026•105.

Нормальная форма представления имеет огромный диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при нали-

8

чии m разрядов у мантиссы и s разрядов у порядка (без учета знаковых

разрядов порядка и мантиссы) будет

Приведем пример. При Р = 2 , m = 2 2 и s = 10 диапазон чисел простирается примерно от 10-300 до 10+300. Для сравнения: количество секунд, к о-

торые прошли с момента образования планеты Земля, составляет всего 1018. Следует заметить, что все числа с плавающей запятой хранятся в машине

в так называемом нормализованном виде. Нормализованным называют такое число, в старшем разряде мантиссы которого стоит единица. У нормализованных двоичных чисел, следовательно, 0,5 ≤ |М| < 1.

Алгебраическое представление двоичных чисел

Знак числа обычно кодируется двоичной цифрой, при этом код 0 означает знак «+» (плюс), код 1 — знак «-» (минус). Для алгебраического представления чисел, то есть для представления чисел с учетом их знака, в вычислительных машинах используются специальные коды:

□прямой код числа;

□обратный код числа;

□дополнительный код числа.

При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания операцией сложения с отрицательным числом.

Дополнительный код обеспечивает более быстрое выполнение операций, поэтому в компьютере чаще применяется именно он.

1. Прямой код числа N — [N]пр. Пусть N = a 1 а 2 а 3...а m

если N > 0, то [N]пр =0,a 1 а 2 а 3...а m ; если N < 0, то [N]пр = 1,a 1 а 2 а 3...а m ;

если N = 0, то имеет место неоднозначность: [0] пр = 0,0... или = 1,0...

Обобщая результаты, получим:

Если при сложении оба слагаемых имеют одинаковый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить большее по абсолютной величине число, произвести из него вычитание меньшего по абсолютной величине числа и разности присвоить знак большего числа.

Выполнение операций умножения и деления в прямом коде выполняется обычным образом, но знак результата определяется по совпадению или несо в- падению знаков участвовавших в операции чисел.

Операцию вычитания в этом коде нельзя заменить операцией сложения с отрицательным числом, поэтому возникают сложности, связанные с заемом значений из старших разрядов уменьшаемого числа. В связи с этим прямой код в компьютере почти не применяется.

9

2.Обратный код числа N — [N]обр.

Обозначение ā означает величину, обратную а (инверсию а),

то есть если а = 1, то ā = 0, и наоборот:

Для того чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа инвертировать, то есть в знаковом разряде поставить 1, во всех значащих разрядах нули заменить единицами, а единицы — нулями.

3.Дополнительный код числа N — [N] доп :

Для того чтобы получить дополнительный код отрицательного числа, необходимо все его цифры инвертировать (в знаковом разряде поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы — нулями) и затем к младшему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд к числу следует прибавить единицу в младший разряд.

Например, N = 0,1011, N[ ]доп = 0,1011; N = –0,1100, N[]доп = 1,0100; N = 0,0000, [N]доп = 10,0000 = 0,0000 (1 исчезает). Неоднозначности в изобра-

жении 0 нет.

Обобщая, можно записать:

СОВЕТ -----------------------------------------------------------------------------------------

Эмпирическое правило: для получения дополнительного кода отрицательного числа необходимо инвертировать все символы этого числа, кроме последней (младшей) единицы и тех нулей, которые за ней следуют.

--------------------------------------------------------------------------------------------------

10