Elementy_teorii_grafov_2

Федеральное агентство по образованию

Ярославский государс венный университет им. П. . Демидова

Êà åäðà òеоретической ин орматики

В. С. ублев

Элементы теории гра ов.

(ин и и у льныДеревья,оты • 8сети9 по исциплин

¾Îñíî û èñêð òíîé ì ò ì òèêè¿)

Ì òî è÷ ñêè óê íèÿ

мендовано

à

Научно-методическим советом

82

екомендовано

едакционно-издательским советом университета

в качестве учебного издания. План 2009/10 года

ка едра теоретической

ецензент

Ярославского государственного

университетин орматикиим. П. . Демидова

82

ублев, В. С. Элементы т ории гра ов. Деревья, сети:

ето . указания / В. С. ублев; Яросл. гос. ун-т. П. . Де-

ìидова. Ярославль: Яр У, 2010. 80 с.

индивидуаль

Мето ические указания содержат

íûõ

заданий по

Äåð

âüÿ ,

Потокиварианты

ÿõ , Ñåòè

èç

плины

Основы дис-

êðåò

математикитемамэлементо, акж необх

мый материал для ее

с мостояте ьного изуче ия

èíä

альных

çà

аниункциональныхой. Д чественного усвоеныполнениякурса в издании даны

ïîäробные определения, примеры,дисц

видуобоснова

.

Предназначены для студентов, обучающихллюстрациия по специаль-

ти 010400.62 Ин ормационные технологии (дисциплина

Îñновы дискретной математики , блок ОП), очной ормы

обучения.

Ó

519.

ÁÁÄÊ Â127ÿ73

Ярославский

государственный

университет

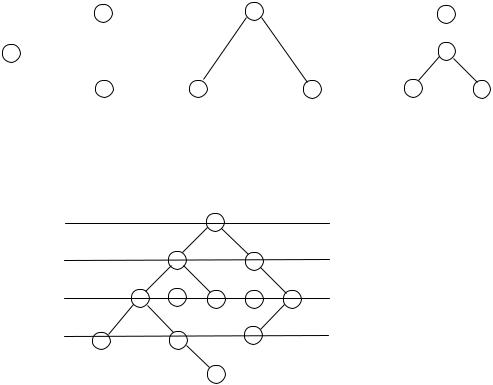
1.1 Определение деревьев и их свойства

ПримерыД р о деревьевназываетсячисломсвязныйвершингра , неn отсодержащ1 до 4 изображеный циклов. на

ðèñ. 1.

èñ. 1

Дерево можно изобразить как иерархическую схему следующим об-

разом:

0

2

5

7

1

10

6

12

2

1

3

3

4

11

8

9

1)

4

èñ. 2

âñå âåðøины располагаются на нескольких уровнях с номерами

2)

0, 1,. . . ;

высоком) находится только 1 вершина она

уровне 0

3)

зывается

(самом дерева;

íà уровне 1

корненах дятся все вершины, смежные с вершиной уровня

4)

0;

каждом

уровне с номером k = 2; 3; : : : нах дятся

находятся ужследующемна уровне k 2;

все вершины, смежные с вершинами уровня k 1, которые не

3

Íà

с. 2 приведен прим р иерархиче

é

хемы для дерева D с 12

ffвершинами,1; g; f1; 4gзаданного; f1; 11g; f2следующим; 3g; f2; 5g; fсписком2; 10g; f5ребер:; 7g; f6; 7g; f7; 12g; f8; 11g;

f9;12gg:

дерево с выделенной

качестве к

èíîé íàçû-

де ева. Такое

Отметим, что

качестве корня

îæíî

ыбрать любую вершину

ваетс

корневым

. В корневом дереве каждая

вершина,

корня, смежна лишьдеревос дной вершиной, находящейс

на более высоккроме

уровне (с номером на 1 меньше), которая называетсорня

òöîì ýòîé âåð-

шинысвяз вающий ее с корнем дерева. Поэтому вершèí

ê

рневого

,

. Äëÿ ê

вершины определяется ед

маршрут

аходящиеся нааждойдном уро не, не смежны между ственныйсобî (предполодерева

имеющиедногосвязывающихдного того ж

îòöà,

азываютс братьями .

противного

дит к циклу, который состоит из ребра между

ì

приво

того же отцавершинызываютс,

его сыновьями

Вершины, не имеющие сыновей, называются

èëè

íèìè

аршрут в,

ý è

корнем). Все вер-

связаны

корнем

эту вершину,листьямиляетс поддеревовисячими. В

вершинами. Для каждой

шины дерева x, не

я листо

1

,

сыновьямичерезве шины x,

называютсявляющейсми, выходя-

часть гра а, образованная этой вершиной

семи вершинами, ко-

этом поддереве вершина x иг ает роль корня,

поддеревья вершины x,

отбразованныех жести с деревом-растением, если перевернуть иерархическую

ùè

и из вершины x. В целом термины корень,

ветви,листья идут

схему.

Свойства деревьев:

любые 2 вершины дерева, является про

1.

стой цепью,связывающийтак как предположении, что есть еще дин марш-

Маршрут, мы приходим к циклу, которого не может

существовать

â

дереве.

2. Колич ство n вершин и количество m ребер дерева связаны со-

1

отношением:

m = n

1:

Иногда применяется терминология

ì òü, î÷ü, ñ ñòð .

4

междудлясвязываеткаждоймножествомвершинынекоторуювершиндерева,вершинубезкромеорнядеревакорня,и множествомñîòåöее отцомединственный,реберàêóñòàêàêòî

навливается 1-1с.

3. Связный гра , имеющий n 1 ребро, является деревом. Дей-

ствительно, в пр дполож

÷òî ýòîò

гра не является

райней мере, 1 ребро так,

он станетссвязныйязным. Будем ис-

деревом, он имеåò öèêë,

ении,из этого

можно исключить, по

êлючать

акие ребра до техчтоп р, покциклавсе циклы не исчезнут,

гра останется связным. Тогда это будет

дерево,

имеющее числно

ребер меньше, чем n 1, что противоречит предыдущему свой-

ству дерева.

циклу этим реб

4. Добавление любого ребра к дереву приво

ð ì,

ò

следу

из свойства 2 (а дитакже следует из свой-

ства 1,чтоакакж

появляется второй маршрут, связывающий концы

добавленного ребра).

Для ориентирова ных корневых деревьев применяют 2 способа ори-

ентации:отцов к сыновьям и

1)2

îò сыновей к отцам.

1.2

Способы задания деревьев

,

Кроме описанных анее способов задания гра а (список

матрица смежности

верш н, матрица инцидентности вершин и ребер)

применяют еще 2 специ èческих для деревьев спос ба:

1. Список отцов для каждой вершины с номером i = 1; : : :; n

i-м месте

находится номер отца этой вершины, если оíà

íå

яспискорнем дерева, или 0 для корня дерева.

Так,являетсвышеописанном примере

ðåâà,

списком ребер,

список отцов будет выглядеть следующимзаданногообраз м:

(2; 5; 2; 1; 0; 7; 5; 11; 12; 2; 1; 7):

5

êðæÿаждойì ýòèõöà âåðøупорядочиваютсявершисыíû)ìспискасамыйбратьевв списоквый, с наименьшимследующаябратьевэтом списк(например,номером),сын ïî íîìåäëÿ

åòñÿ

ледующè

брато(наприм. Для каждой вершины спискназывает

братьев

íîìå îì i

= 1; : : : ; n

i-ì

стевершинасписксыновейнах

сыновей)старшимледующèé

áð

ñî ñëìåдующим по поряд-

нет, то записывается(вершина0, если нет

ледующего бр

,

дится пара

старш

ñûí

ñ íàè

ньшим

номер

ì èç

ку возрастания номером

брата) для этой вершины. Если сыновей

вершиныо акж записывается 0.

Так, для вышеописанного примера дерева список сыновей иатабр -

òüåâ

будет выглядеть следующим образом:

((4; 3); (1; 7); (0; 10); (0; 11); (2; 0); (0; 12); (6; 0); (0; 0); (0; 0); (0; 0);

(8; 0); (9; 0)):

åíèå

Список отцов удобен для алгоритмов, в которых идет

дереву снизу ввер , а список сыновей и братьев удобендвижтех алго-

ðè ìàõ,

оторыхудобно оба списк совместитьвнизодин спис к отцов,

ê

движение по дереву идет

направпо.

направлениях,сыновей братьев. Так, для

вышеописанного примера такой список

 òåõ æ

случаях, когда движение может происх

тьслеваразличных

отцов, сыновей и братьев будет выглядеть следующим образом:

((2; 4; 3); (5; 1; 7); (2; 0; 1 ; (1; 0; 11 ; (0; 2; 0); (7; 0; 12); (5; 6; 0); (11; 0; 0);

(12; 0; 0); (2; 0; 0); (1; 8;0)); (7; 9; 0)):

Еще 1 способ относится к заданию специальных деревьев бинар-

ных деревь в, каждая вершина которых имеет не более 2-х сыновей. В

этом случае для каждой

ÿ

èç

левого

и правого сына; если к

ого-то сына нет то всписокчестве номера задает-

ся 0. Список сыновей акор я

спискзадаетсбинарного дерева нах дится на

первом месте. Так, для бивершиныарного дерева, заданного спискномеровсыновей

и братьев

((2; 0); (4; 3); (6; 0); (8; 5); (0; 0); (0; 7); (9; 0); (0; 0); (0; 0))

список бинарного дерева будет выглядеть следующим образом:

((2; 3); (4; 5);

(6; 7);

(8; 0); (0;60); (0; 0); (0; 9); (0; 0);

(0; 0)):

Деревья очень часто используются в различных дискретных зада

пиляция÷àõ. Íî êäíèäàèçïðèсамыхт ансляцииважныхвыражен

языкове приложений это к

где используется деðево выраженийин, орматикн ормационныйпрограммирования,поиск, омк -

тором важную роль играют поисковые деревья.

1.3.1

Дерево

åíèé

ассмотрим выражк честве примера ари метическое выражение

(a + b) + a (b d):

Его можно представить

âèäå

где корнем дерева является

оследняя

операция,дерева,2

, идущие из корня,

2 поддерева выражений

операциè корня. Продолжая

процесс, мы

троим дерево выражениветв,

котором листьями будуэтот

символы a; b; ; d,

ëþáàÿ операция выражения вер-

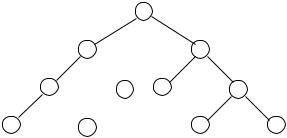
терминальныешиной, яввыполняемаяющейс листом

де ева. На рис. 3 изображено дерево

выражения

äëÿ вышеуказанногоопеðàíäîâðимера.

a

+

*

+ a

/

d

b

èñ. 3

b

Дерево выражения оïðеделяет все возможные способы вычисле-

íèÿ âû àæ

. При этом вычисления идут по дереву снизу вверх.

Äëÿ

опред

ления

значения к

вершины сначала вычисляются

çíà

ñûí â é-

аждойзатем берется от них ункция, со-

îïåрацииоперандов,вершине (+; ; ; =). Т

образом од а

из задачения обойти все вершины дерева, побывав акимв аждой вершиíå

ответствующаяраньше, чем ее отце.

7

ями (например, ари метических выражений) называется

í èêñí é

äîâ,записüþ:выраженîï ðàöя постй,я записываетсяприи от йромзаписьюоперациямежду. Îíàоперандамиидет после. Другойсвоихя приоперанспособх де

вершназываетсдерева

снизу

вверх

слева направо. Так, для вышеописанно-

ãî

ïðè

åðà

выражения

пост иксная

запись выражполучается следующим

образоì:

a b +

a b d

=

+ :

я бесскобочной.

З метим, что пост ксная запись выражения

чения выражения мо но легк

ганизоватьявляетспомощью

ñòåê

ïðè

Ò êîé âèä

åíèÿ

непривычен и ненагляден. Однак

вычисление

çíàск нировании выражения слева направо:

2) если элемент выражения знак операции, то из стекзаписываемизвлекаем

1)

не знак операции, то

åãî

â ñòåê;

записанных опер нда,

операцию

этими

2

последнихами результат записывàåì â ñòåê.

стек будут записаны опе-

Ò

êèì

для выражения сначала

умнож

запишетсстек будут извлеченывыполняемопера ды a + b, а в стек за-

ранды aобразом,b затем при

и операции сложения эти операнды

будут

стека,выполнена стек запишетс

a + b.

Затем извлеченыстек будут записаны a; b; d, и при

выполнении последующей

Затем

ñòåê

ÿ ,

ïðè

выполне

следующей операции

пишетсения(a + b) .

из стека будут извлечены операнды d

b, à â

операции вычитания

стек за ишется b d.

b) , а в стек запишется

дут извлеченывыполненииеранды a=(b d)

Затем

ïðè

следующей операции

èç ñòåê

будут

извлечены операнды b d и a, а в стек запишетсделенияa=(b d).

áó-

Наконец, при

олнении последней операции сложения из стек

При компиляции

программ ого к да

подобный алго

окончательный результат выражения (a + b) + a (b d):

вместо

выражен я

оизводитсвыполняетсциягенерà

команды ком-

ритм, но вместо записи

стек записыв ются их

ðåñà, à

пьютеравычислениясоответствующимоперандовè ад есами операндов.

8

альный обход

ения. Приведем алгоритм, использующий

способ1 В кзаписичестведеревавыражначальногоâèäåзначениясписка отекущейцов, сыновейвершиныбратьеввыбираем.

êî

2o:

ðåíü.

нет сы овей, то выписываем ее и пе-

Åñëè ó

реходим

пункту 3o, аче к пункту 5o.

брат, то выбираем его

3o: Åñëè ó

текущейвершиныесть

в качестве текущей вершины

следующийпереходим к пункту 2

o

; иначе

переходим

пункту 4o.

4o: Åñëè ó

текущей

ершины нет отца, то выполнение алгоритма

o

закончено; иначе

â качестве текущей вершины выбираем отца,

5

:

м ее и переходим к пункту 3o.

выписываВ к честве

текущей вершины выбираем старшего сына и пере-

1.3.2

ходим

пункту 2

o

.

Поисковое дерево

я часто орг низуется в специаль

í

Для быстрого поиска ин орма

ин ормацию

снабжается специальной записью (число или стро

ое поисковое бинарное дерево, в котором каждая вершина указывает

следующийпоисковыйалг ритм:

ê

символов), называемой ключом вершины. При поиск ин ормации

задается

ключ и ищется вершина, значение ключа кото-

рой совпадает со значением поискового ключа. Для этого выполняется

1

 êà

текущей вершины выбирается корень дерева.

2.

Значенчествепо скового ключа сравнивается

ключом текущей вер-

3.

øèíû, è

они совпадают, то поиск успешно

.

Если значен

поискового ключа меньше, то в кзавершенчестве текущей

вершины

выбирается левый сын, если он есть, и переходим на

пункт 2;

если его нет то поиск завершен

неуспешно.

9

вершины выбирается правый сын, если он есть,

переходим на

Для выполненияпункт 2; еслитакогоåãî íåòалгоритмато поискспискзавершенби неуспешнодерева.

каждый

элем нт помимо сп ск

сыновей имеет ключ, нахрногодящийся на первом

ìåñòå. Пусть,

например, имеется

массив ключей

f1; 3; 4; 7; 12; 13; 15; 19; 20g:

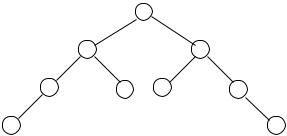
Пусть бинарное поисковое дерево задано следующим списком (рис. 4):

(

2; 2; 3); (4 4 5); (15; 6; 7); (3; 8; 0); (7; 0; 0); (1; 0; 0); (19; 0; 9);

(1; 0; 0); (20;0;0) ):

2 4

1

12

15 3

4

3

5

13

19 7

8

1

7

6

209

Ïðè

èñ. 4

êëþ-

ключа 7 он будет по ледовательно

сравн ваться

чами 12,поиск4

7,

поиск законч тся

. При поиск

14

он будет

яспешноключами 12, 15, 13,

èñê

закончится неу пешно. Носравниватьсэтом случае может быть

добавленключавая

вершина последовательнопои овое дерево, как правый сын вершины с последним

при ср внении ключом

13.

 ê ÷åñ âå

используются не обязательно бинарные де-

ревья. В этом случаеовых ршиной, имеющей m сыновей, связывается

óïîð

поисквозрастанию последовательность из m 1 ключа,

проядоченнаясх

тех пор, сравнениепок

искового ключа

этими

ключами вершины

îâûé

ключ не попадет

äèí

èç mäèò

последовательноена к рые эт ми ключами

ÿ âñå

жные значения. После

этого происпоискх дит переходразбиваютск сыну рши-