Практическое руководство для студ. экон. спец. 3 ч

Теорема 2.3. Пусть функция f x непрерывна на отрезке [a;b]. Тогда, если функция F(x) является некоторой её первообразной на этом отрезке, то справедлива следующая формула

b
f (x)dx = F(b ) – F(a).	(2.6)

a

Эта формула называется формулой Ньютона-Лейбница.

Формула (2.6) не только устанавливает связь между определённым и неопределённым интегралами, но и даёт простой метод вычисления определённого интеграла.

1	x	3		1		1
Пример 2.2. x2dx =					=		.
0	3			0	3

2.3 Основные методы интегрирования

К таким относятся методы: замены переменной; интегрирования по частям.

Теорема 2.4. (о замене переменной в определённом интеграле).

Пусть	f x – непрерывная функция на отрезке [a;b]. Тогда если: 1)
функция x	= φ(t) дифференцируема на [ ; ] и φ'(t) непрерывна на [ ; ]; 2)
множеством значений функции x		= φ(t) является отрезок [a;b]; 3) φ( ) a,
φ( ) b, то справедлива формула
	b		(2.7)
	f (x)dx = f ( (t)) (t)dt.
	a

Формула (2.7) называется формулой замены переменной или

подстановки в определённом интеграле.

Замечание 2.1. Если при вычислении неопределённого интеграла с помощью замены переменной мы возвращались от новой переменной к старой, то при замене переменной в определённом интеграле делать этого не надо.

									3		x
		Пример 2.3.												dx
= t									0		x 1															x 3,t 2,т.е. 1, 2 =
							1,dx 2tdt;при											x 0,t 1,при
				x 1,x t2
2	t	2	1				2									t	3				2			8				1			8
								2
=					2tdt 2 t				1dt			2						t				=	2		2			2		1			.
																3					1
1			t				1																3					3		3

Теорема 2.5. (об интегрировании по частям в определённом интеграле).

Если функции u x и v x непрерывны вместе со своими производными u x и v x на a;b , то справедлива формула

b	b	b	(2.8)
udv uv	a	vdu.
a		a

11

Формула (2.8) называется формулой интегрирования по частям в

определённом интеграле.

e

1

Пример 2.4. nxdx u nx,dv dx,du

dx,v

dx x =

1

x

= nx x

e

e

1

dx e 0 x

e e e 1 1.

x

1

1

x

1

2.4 Приложение определенного интеграла

2.4.1 Площадь криволинейной трапеции

Определённый интеграл от неотрицательной непрерывной

функции

f x на

a;b

равен

площади криволинейной трапеции, ограниченной

сверху графиком функции y f x , слева и

справа прямыми

x a,x b,

снизу осью Ox .

Пример 2.5. Найти площадь фигуры, ограниченной графиком функции y x2 , прямой x 1 и осью Ox (Рисунок 2.2.).

1	2		x3		1	1
Решение. S x		dx						.
			3		0
0						3

Более сложные задачи на вычисление площадей, решают, используя свойство аддитивности площади: можно разбить фигуру на непересекающиеся криволинейные трапеции и вычислить площадь всей

фигуры как сумму площадей этих частей.
Пример			2.6.	Найти	площадь				фигуры,						ограниченной											линиями
y x, y	1	, y 0, x 3 (Рисунок 2.3.).
	x2
Решение. S S1				1	3	1		dx=	x2		1	1			3	1				1		7			.
				S2 xdx																	1
							2
				0	1	x			2		0	x			1 2					3 6
Если на a;b заданы две непрерывные											функции								y1	f1 x и						y2 f2 x ,
причём при всех значениях x a;b									верно			y1			y2 ; то площадь фигуры,
ограниченной			сверху графиком функцииy2 f2 x ,																снизу							графиком

12

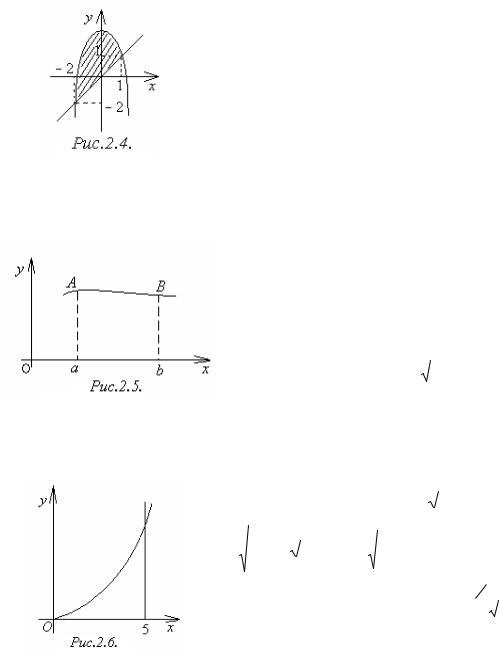
функции y1 f1 x , слева и справа прямыми x a, x b, вычисляется по

b

формуле S f2 x f1 x dx.

a

Пример 2.7. Найти площадь фигуры, ограниченной графиком функции y x и y 2 x2 (Рисунок 2.4.).

Решение. Найдём точки пересечения графиков данных функций:

y x

2y 2 x

2 x2 x, x2 x 2 0, x1 2,x2 1.

A 2; 2 , B 1;1 .

					1					x dx
Тогда S 2 x2											=
					2
			x3			x2			1		1		1			8			1
=		2x								= 2				4				1 4 .
			3		2				2		3					3
													2						2

	2.4.2 Длина дуги кривой
																Пусть									плоская									кривая										задана								уравнением
															y f x ,						где					f x непрерывная на																									a;b				функция.
															Если производная																f					также непрерывна на a;b ,
																																	x
															то длина дуги												AB				данной кривой (Рисунок 2.5.)
															вычисляется по формуле
																																	b												dx.
																													L									1 f 2 x
																																	a
															Пример 2.8. Вычислить длину дуги
																	3
полукубической параболы y x																					от x 0						до x 5 (Рисунок 2.6.).
																			2
													Решение. Найдём																				3
																																							x . Тогда
																											y x						2
														5		3								2		5																9								9												4
																														9
														L		1					x			dx=			1						xdx = 1											x t,							dx	dt			,dx									dt ,
																																										4								4												6
														0		2										0				4
																																								49																	3			49
													при x 0				t 1, при x 5																			49				=		4						4	dt=			4		t2									=
																															t															t
																																																													4
																																				4																9				3
																																												9																1
																																										1
							3							3			8				343						335																											2
	8				49 2						8			7
=								1							1 =											1							.
	27				4						27		2				27				8						27

2.4.3 Площадь поверхности вращения

13

Пусть кривая AB задана уравнением y f x ,

a x b, и пусть функция

y f x

неотрицательна

и

непрерывна

вместе

со

своей

первой

производной

на

a;b . Тогда поверхность, образованная

вращением

кривой

AB

вокруг

оси

Ox

(Рисунок 2.7.), имеет площадь S , которая

может быть вычислена по формуле:

b

S 2 f x

1 f 2 x

dx.

a

Если же поверхность получается вращением кривой

AB,

заданной

уравнением x y ,

c y d ,

вокруг

оси

Oy ,

то

площадь такой

d

поверхности вычисляется по формуле

S 2 y

1 2 y

dy.

c

Пример 2.9. Часть сферы, вырезаемая двумя

параллельными плоскостями, находящимися на

расстоянии

H друг от друга,

называется шаровым

поясом высоты H . Вычислить площадь шарового

пояса высоты H , если радиус шара равен R (Рисунок

2.8.).

Решение. Поверхность шарового пояса можно рассматривать как поверхность, полученную при вращении дуги

окружности y

R2

x2 , где

a x b, b a H , вокруг

оси

Ox (Рисунок

2.9.).

Так как

y x

x

, то

R2 x2

2

x2

R2

1 y

x 1 R2 x2 R2 x2 .

b

R

b

Тогда

S 2 R

2

x

2

dx=

2 Rdx=

R

2

x

2

2 R b a 2 RH . В частности,

a

a

если

H 2R,

то

получаем

площадь

поверхности сферы S 4 R2 .

2.4.4 Объём тела

Рассмотрим некоторое тело и вычислим

его объём V . Допустим, что известны

площади сечений этого тела плоскостями,

перпендикулярными оси Ox . С изменением

x

меняется и площадь сечения, т.е. площадь

сечения

является

некоторой

функцией

S S x .

Если эта

функция непрерывна на

14

b

a;b , то объём тела V S x dx.

a

В частности, если тело образовано вращением вокруг оси Ox

криволинейной трапеции,	ограниченной сверху дугой AB		непрерывной
линии y f x , где a x b	(Рисунок 2.10.), то	S x f x 2	и получаем
b
формулу V f 2 x dx.
a
Если же тело получено вращением вокруг		оси Oy криволинейной
трапеции, ограниченной дугой CD линии x y ,		c y d , то его объём
	d
	V y 2 dy.

c

Пример 2.10. Вычислить объём тела, полученного вращением вокруг оси Ox криволинейной трапеции, ограниченной линиями xy 6, x 1, x 6

(Рисунок 2.11.).

Решение.

	6					6		36
V y2dx=										dx=
								2
	1					1		x
		36			6					36
=					1	= =							36		30 .
		x								6

Вопросы для самоконтроля

1.Укажите задачи, приводящие к понятию определенного интеграла.

2.Что называется определенным интегралом от данной функции на данном отрезке?

3.Каков геометрический смысл определенного интеграла от данной функции y = f(x) на отрезке [a, b] в системе декартовых координат?

4.Сформулируйте простейшие свойства определенного интеграла.

5.Сформулируйте теорему о среднем в интегральном исчислении.

6.В чем заключается теорема об оценке определенного интеграла.

7.Чему равна производная от интеграла по его верхнему пределу?

8.Напишите формулу Ньютона — Лейбница.

9.В чем состоит метод замены переменной (метод подстановки) в определенном интеграле?

10.В чем состоит метод интегрирования по частям в определенном интеграле?

11.Как вычисляется площадь плоской фигуры в системе прямоугольных координат?

15

x a. Рассмотрим

12.Как вычисляется длина дуги в прямоугольной системе координат?

13.Напишите формулу для вычисления площади поверхности вращения.

14.Напишите формулу для вычисления объема тела.

3 Несобственные интегралы

3.1 Интегралы с бесконечными пределами (несобственные интегралы первого рода)

При введении понятия определённого интеграла предполагалось, что выполняются условия: 1) пределы интегрирования a и b являются конечными; 2) подынтегральная функция f (x) ограничена на a;b . В этом случае определённый интеграл называют собственным. Если хотя бы одно из двух указанных условий не выполняется, то интеграл называют

несобственным.

Пусть функция y f (x) непрерывна при любом определённый интеграл с переменным верхним пределом

b

Ф(b) f (x)dx.

a

Предположим, что при b функция Ф(b) имеет конечный предел;

этот предел называется сходящимся несобственным интегралом от

функции f (x)	по промежутку a; ) и обозначается
		b	f (x)dx .
		f (x)dx im
		b
	a	a
Если же	этот предел не	существует	или равен бесконечности, то

несобственный интеграл называется расходящимся.

Геометрически несобственный интеграл от неотрицательной функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции y f (x), слева прямой x a, снизу осью Ox (В случае сходящегося интеграла эта площадь является конечной, в случае расходящегося бесконечной) (Рисунок 3.1.).

Если F(x) первообразная для f (x), то

		b	f (x)dx = im F b F a =
	f (x)dx im
	b			b
a		a
=F( ) F(a) , где				F( ) = im F(b).
				b

и несобственный интеграл с обоими бесконечными пределами

16

b		b	f (x)dx и несобственный интеграл с обоими бесконечными
	f (x)dx im
	a
		a
			c
пределами			f (x)dx	f (x)dx + f (x)dx,	где с любая точка из интервала
				c

; .

dx

b

dx

b

Пример 3.1.

=

= im

=

.

im

arctgx

im arctgb arctg0

2

2

0

0

1 x

b

0 1 x

b

b

2

Пример 3.2.

b

im

b

= im sinb

sin 0 =

cosxdx im

cosxdx

sin x

0

b

0

b

0

b

im sinb . Этот предел не существует, следовательно, интеграл расходится.

b

Пример 3.3.

0

exdx exdx+

exdx. Этот интеграл расходится, так как

0

b

b

exdx=

exdx=

im

im

ex

0

= im eb 1 = .

0

b

0

b

b

С помощью следующих двух теорем можно исследовать вопрос о

сходимости некоторых несобственных интегралов.

Теорема 3.1. Если при

x a выполнены неравенства 0 (x) f (x) и

f (x)dx

сходится, то сходится и (x)dx , причём (x)dx f (x)dx ;

a

a

a

a

если же (x)dx расходится, то расходится и интеграл f (x)dx .

a

a

Теорема 3.2. Если в промежутке a; функция

y f (x) меняет знак и

f (x)

dx сходится, то сходится также

f (x)dx .

a

a

3.2 Интегралы от неограниченных функций (несобственные

интегралы второго рода)

Если функция y f (x)

не ограничена в окрестности точки с отрезка

a;b и непрерывна при a x c

и

c x b, то несобственный интеграл от

этой функции определяется формулой

b

f (x)dx = im

c

f (x)dx+ im

b

f (x)dx,

где 0, 0

(3.1)

0

0

a

a

c

В случае, когда c b или c a , получаем

b

f (x)dx = im

b

(3.2)

f (x)dx

0

a

a

b

f (x)dx = im

b

(3.3)

f (x)dx

0

a

a

17

Несобственный интеграл (3.2) или (3.3) называется сходящимся, если существует конечный предел соответствующего определённого интеграла; в противном случае интеграл называется расходящимся. Несобственный интеграл (3.1) называется сходящимся, если существуют и конечны оба предела в правой части.

Для интегралов от неограниченных функций справедливы теоремы, аналогичные теоремам 3.1. и 3.2.

1

Пример 3.4. dx , 0 некоторое число.

0 x

1	dx			1	dx				x1			1
1) Если 1,то			= im				= im							=
0	x		0		x		0 1

,при 0

=1

1 ,при 0 1

1	dx			1	dx			1
2) Если 1, то		=				= im				=
			im				nx
					x
0	x		0			0

		1	1		=
im
		1
0

im n .

0

Таким образом, данный интеграл сходится при 0 1 и расходится при

1.

Вопросыдлясамоконтроля

1.Какой интеграл называетсянесобственным?

2.Какой интеграл называется несобственным интегралом первого рода? Приведите примеры.

3.В каком случае несобственный интеграл первого рода сходится (расходится)?

4.Какой интеграл называется несобственным интегралом второго рода? Приведите примеры.

5.В каком случае несобственный интеграл второго рода сходится (расходится)?

4 Функции нескольких переменных

4.1 Функции нескольких переменных

Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.

Определение 4.1. Пусть имеется n переменных величин, и каждому набору их значений (х1,х2,...,хn ) из некоторого множества X соответствует одно вполне определённое значение переменной величины z. Тогда говорят, что задана функция нескольких переменных z = f (х1,х2,...,хn ).

18

Пример 4.1.	Формула	V = R2H			задаёт объём цилиндра V как
функцию двух переменных V(R;H), где R − радиус основания, H − высота
цилиндра.
Переменные х1,х2,...,хn		называются независимыми переменными или
аргументами, z	зависимой переменной, а символ f означает закон
соответствия. Множество X называется областью определения функции.
	Пример			4.2.	Область определения		функции
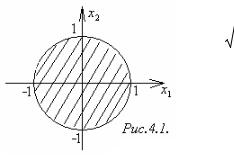
	z =			задаётся условием 1 x12 x22 ≥ 0
		1 x12 x22
	или	x12 x22 ≤		1.	Эта область	представляет собой
	единичный круг с центром в начале координат и
	радиусом 1 (рисунок 4.1).
	Рассмотрим				некоторые	примеры	функции

нескольких переменных:

1.Функция z = a1x1 a2 x2 ... an xn , где a1 a2 ... an , b − постоянные числа, называется линейной.

		1	n	n
	2. Функция z =		bij xi xj , где bij − постоянные числа,		называется
		2 i 1		j 1
	квадратической.				функция
	3.Одно из базовых			понятий экономической теории −

полезности. Эта функция z = f (х1,х2,...,хn ), выражающая полезность от n приобретённых товаров х1,х2,...,хn . Чаще всего встречаются следующие её виды:

n				0, xi	ei 0, − логарифмическая функция;
а) z = ai n(xi ei ) , где ai
i 1
n	a	1 bi					xi ei 0 − функция
б) z =	i	(xi ei)	,	где	ai 0,	0 bi 1,
	1 b
i 1	i

постоянной эластичности.

4.Также часто в экономике встречается понятие производственной функции, выражающей результат производственной деятельности от обусловивших его факторов. Например, при n = 2 для величины общественного продукта z = b0x1b1 x2b2 , где x1 − затраты труда, x2 − объём производственных фондов, b0 ,b1,b2 − постоянные числа.

В дальнейшем будем вести изложение для функции двух переменных (n = 2). При этом, практически все понятия и теоремы, сформулированные для n = 2, легко переносятся и на случай n > 2 кроме того, рассмотрения двух переменных позволяет использовать наглядную иллюстрацию.

19

4.2 Предел и непрерывность функции нескольких переменных Определение 4.2. Множество всех точек М(x; у), координаты которых удовлетворяют неравенству

(x x0 )2 (y y0 )2 , называется − окрестностью

точки М0(х0; у0) − это всё внутренние точки круга с центром М0 и радиусом (рисунок 4.2).

Определение 4.3. Пусть функция z = f (x;y) определена в некоторой окрестности точки М0(х0;у0), кроме быть может, самой этой точки. Число А называется

пределом функции z =

f (x;y)

при x x0

и y y0

(или, что то же самое,

при М(х; у) → М0(х0; у0)), если для любого > 0

существует 0 такое,

что для всех

x x0 и

y y0

из

−окрестности точки М0, выполняется

неравенство

f (x; y) A

. Записывают:

А = im f (x; y)

или

А = im

f (M).

x x0

M M0

y y0

Пример 4.3. Найти

im

n(1

x2

y2 )

.

x 0

x

2

y

2

y 0

Решение. Обозначим

=

. Тогда

условие

x 0;

x2

y2

y 0

равносильно тому, что 0. Теперь

1

( 2 )

n(1 x2 y2 )

n(1 2 ) 0

1 2

2

im

= im

=

im

= im

0.

1

2

1

x

y

y 0

2

2

0

0

0

0

x 0

Как правило, вычисление пределов функции двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что на прямой существуют всего 2 направления, по которым аргумент может стремиться к предельной точке − а именно, справа и слева. На плоскости же таких направлений − бесконечное множество, и пределы функции по разным направлениям могут не совпадать.

Пример 4.4. Найти предел функции im

x2

y2

.

x2

x 0

y2

y 0

Решение. Будем приближаться к точке О(0;0) по прямым y kx. Тогда

im

x2

y2

=

im

x2

k2 x2

=

im

1 k2

=

1 k2

.

Меняя значения k , будем

x2

x 0

y2

x 0 x2

k2 x2

x 0 1 k2

1 k2

y 0

получать равные значения предела. Это означает, что данный предел не существует.

Предел функции двух переменных обладает свойствами, аналогичными свойствами предела функции одной переменной.

20