Министерство образования и науки Российской Федерации Балтийский государственный технический университет «Военмех»
С.Д. ШАПОРЕВ, Б.П. РОДИН
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Учебник
Допущено научно-методическим советом по математике вузов Северо-Запада
в качестве учебника для студентов вузов, обучающихся по направлениям 160403 – Системы управления движением и навигация; 200200 – Оптотехника; 210300 – Радиотехника; 230100 – Информатика и вычислительная техника; 230200 – Информационные системы
Санкт-Петербург
2010
УДК 519.216:519.876.5:004.42-027.22(075.8) Ш 24
Шапорев, С.Д.
Ш 24 Случайные процессы: учебник / С.Д. Шапорев, Б.П. Родин; Балт. гос. техн. ун-т. – СПб., 2010. – 237 с.
ISBN 978-5-85546-499-3
Рассмотрены основы теории случайных процессов. Описаны важнейшие модели процессов с дискретным и непрерывным временем, их действие на линейные стационарные системы автоматического управления, а также методы математического моделирования случайных процессов. Рассмотрены решения типовых примеров, поясняющих теоретический курс, приведены семь лабораторных работ, выполняемых в двух математических пакетах: Mathcad и Matlab.
Для студентов и аспирантов технических университетов, обучающихся по радиотехническим специальностям. Книга может быть полезна преподавателям, читающим соответствующие курсы.
УДК 519.216:519.876.5:004.42-027.22(075.8)
Ре ц е н з е н т ы: кафедра математического моделирования
иоптимизации химико-технологических процессов СПбГТИ (ТУ) (зав. каф. д-р техн. наук, проф. В.А. Холоднов); д-р техн. наук,
проф. М.С. Попов
ISBN 978-5-85546-499-3 |
© С.Д. Шапорев, Б.П. Родин, 2010 |
|
© БГТУ, 2010 |
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
1.1. Случайные процессы. Основные определения
Случайной функцией называется семейство случайных величин, зависящих от параметра t , t T , T – произвольное множество.
Пусть (Ω, М, P) – вероятностное пространство, t – параметр, t T , ω Ω – элементарное событие. Тогда случайной функцией ξ(t, ω), t T называется измеримое отображение ξ: Ω → Rn про-
странства элементарных событий Ω в Rn , зависящее от параметра t . Когда T – множество действительной прямой, а параметр t интерпретируется как время, вместо термина случайная функция употребляется термин случайный процесс.
Случайный процесс является математической моделью для описания случайных явлений, развивающихся во времени. Процесс, для которого характерно изменение физической величины во времени случайным образом, принято называть случайным или стохастическим. Как видно, он описывается случайной функцией, представляющей собой функцию одного или нескольких аргументов, которая при всех или нескольких значениях этих аргументов является случайной величиной.
Обычно, когда это не приводит к неясности, зависимость ξ(t,ω) от ω не указывается и случайный процесс обозначается просто ξ(t).
Если n =1, случайный процесс ξ(t), t T называется скаляр-
ным случайным процессом, а при n ≥ 2 – векторным или n-мерным случайным процессом. Если T ≡ N , то вместо случайной функции ξ(t,ω), t T употребляется термин случайная после-
довательность, которую обозначают {ξk (ω)}∞k =1 .
Пусть t0 T – фиксированный момент. Случайная величина
ξt0 (ω)= ξ(t0 , ω) называется сечением случайного процесса в точке t0 T . Таким образом, случайный процесс представляет собой не
3
что иное, как систему случайных величин – всех сечений этого процесса. При фиксированном ω0 Ω неслучайная функция
ξω0 (t)= ξ(t, ω0 ), t T , называется траекторией, соответствующей
элементарному исходу ω0 Ω . Часто траектории называются реа-
лизациями или выборочными функциями случайного процесса.
Таким образом, случайный процесс, описываемый случайной функцией ξ(t,ω), – это ансамбль из множества реализаций:
ξω1 (t), ξω2 (t),...,ξωk (t),...
Семейство реализаций случайного процесса – основной экспериментальный материал, на основе которого можно получить характеристики случайного процесса.
Пример 1. Пусть случайный процесс ξ(t) определён формулой ξ(t)= tξ, t [0,1], ξ~ R[0,1]. Найдём множество сечений и траекторий случайного процесса ξ(t).
В данном случае, при фиксированном t0 [0,1] сечение ξt0 (ω)= t0ξ является случайной величиной, имеющей равномерное распределение на отрезке [0,t0 ], т.е. ξt0 (ω)~ R[0,t0 ]. Неслучайные функции ξω0 (t) (траектории процесса) – это прямые линии, выходящие из точки (0,0) со случайным тангенсом угла наклона, равным ξ0 . Все траектории непрерывны (рис. 1.1).
t
Рис. 1.1. Некоторые траектории движения случайного процесса tξ
4
1.2. Элементарная классификация случайных процессов
Поскольку всякая классификация условна, то один и тот же случайный процесс может удовлетворять нескольким квалификационным критериям. Например, случайные процессы могут быть описаны с единых позиций в соответствии с наличием у них тех или иных общих признаков.
1. Классификация по зависимости характеристик процесса от начала отсчёта времени: а) стационарные случайные процес-
сы; б) нестационарные случайные процессы.
Стационарным называется такой случайный процесс, у которого определённая группа вероятностных характеристик инвариантна во времени, т.е. не изменяется при сдвиге времени – замене аргумента t значением t + τ, где τ – произвольный интервал. Различают стационарные в узком и широком смысле случайные процессы.
Случайный процесс называется стационарным в узком смысле, если n-мерное распределение вероятностей не изменяется со временем, т.е. выражения для плотности вероятностей любого порядка не зависят от выбора начала отсчёта:
fn (x1,t1, x2 ,t2 ,..., xn ,tn )= fn (x1,t1 + τ, x2 ,t2 + τ,..., xn ,tn + τ).
Случайный процесс называется стационарным в широком смысле, если его средняя и дисперсия не зависят от времени, а корреляционная функция зависит лишь от разности времени τ . Стационарные процессы, стационарные в узком смысле, стационарны и в широком, но не наоборот.
Наиболее труден для изучения класс нестационарных случайных процессов. Они делятся по различным дополнительным признакам на элементарные, квазистационарные, периодические и почти периодические, аддитивные, мультипликативные, сепарабельные, структурно однородные и т.п. случайные процессы.
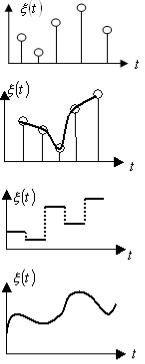
2. Классификация по типу областей существования и изменения случайных процессов (табл. 1).
Это процессы с дискретным и непрерывным временем, с дискретными и непрерывными состояниями. Таким образом, в зависимости от характера множества T и множества состояний слу-
чайной функции ξ(t) такие процессы делятся на четыре подкласса, указанные в табл. 1.
5
Т а б л и ц а 1
Свойства t |
Свойства ξ(t) |
Вид одной реализации |
Примеры |
||||
|
|
|
|
|
|
||
Параметр |
Случайная |
ξ(t) |
|
Цепи |
Марко- |
||
t |
дискретен |
функция |
|
ва |
|
|
|
|
|
дискретна |
|
|
|
|
|
|
|
|
|
|
|||
Параметр |
Случайная |
ξ(t) |
|
Обобщённые |
|||
t |
дискретен |
функция |
|
цепи Маркова |
|||
|
|
непрерывна |
|
|
|
|
|
|
|
|
|
|
|
||
Параметр |
Случайная |
ξ(t) |
|
Потоки |
зая- |
||
t |
непреры- |
функция |
|
вок на обслу- |
|||
вен |
дискретна |
|
|
живание |
в |
||
|
|
|
|
|
системах мас- |
||
|
|
|
|
|
сового |
об- |
|
|
|
|
|
|
служивания |
||
|
|
|
|
|
|
||
Параметр |
Случайная |
ξ(t) |
|
Задачи |
тео- |
||
t |
непреры- |
функция |
|
рии |
управле- |
||
вен |
непрерывна |
|
|
ния |
|
|
|
|
|
|
|
|
|
|
|
3. Классификация по наличию или отсутствию зависимости вероятности распределения координат случайной функ-
ции от её предыстории: а) марковские; б) немарковские. Случайный процесс называется марковским, если его будущее
зависит лишь от настоящего значения и не зависит от прошлого. Более точное определение будет дано позднее в терминах услов-
ных плотностей распределения случайных величин ξti (ω).
Оказывается, что многие реальные физические системы имеют не более чем счётное множество возможных состояний, а их поведение адекватно моделируется посредством марковских процессов.
6