Глава 5

Пример 1. Докажите, что L1 L2
		L1	L2 .

1

2

1

2

Доказательство. Пусть x L

L

.

Тогда y L

L

x, y 0. В

силу того, что

y L L

, y y

y

2

,

где

y

L , а y

2

L

. Следовательно,

1

2

1

1

1

2

x, y x, y1 x, y2

0.

Если в последнем равенстве выбрать

y2

,

то из

условия

x, y1

0

заключаем, что

. Полагая

y1 , получаем, что

x L1

x, y2 0

или

Другими словами, из условия x L1

L2

вытекает,

x L2 .

что

. Тогда

x L1

L2

.Пусть теперь x L1

L2

x, y

y

2

x, y x, y

2

0 , т.к.

x L и

x L

. Значит,

x L L

. Та-

1

1

1

2

1

2

ким образом, мы получили, что если

x L1

L2

, то

x L1 L2 . И, наобо-

рот, если

, то x L1

L2

. Сказанное равносильно равенству

x L1

L2

L1 L2

L1

L2 .

Пример 2. Линейное подпространство

L1

задано системой уравнений:

2x

x

2

3x

3

x

4

0,

1

2x

2x

0,

3x

2

4

1

x

9x

x

0.

3x

2

3

4

1

Найдите базис ортогонального дополнения

L1 .

Решение. Найдем базис

L1

. Для этого решим данную однородную систему

уравнений:

2 1						3 1						1			1 3					1		1			1		3		1			1
3 2						0 2						~		3 2 0						2		~	0		1		9		1		~			0
																1 9									2		18
3 1						9 1						3								1		0							2			0
dimL			1	n r 4 2 2;
x3		, x4	- свободные переменные;
x	2	9x			3		x	4	;
x x						2	3x			3	x		4	9x		3	x	4		3x	3	x	4	6x		3	x		6x			3	.
		1																									1
Таким образом, общее решение имеет вид:																											6x	3	,9x	3	x			4	, x	3

1	3	1
1	9	1	;
0	0
		0

, x		T	. Выбирая
4

значения свободных переменных в соответствии с таблицей

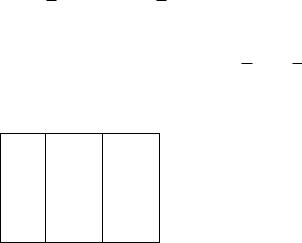
	i	x	i	x	i
			3		4
	1	1		0
	2	0		1

получаем базисные векторы подпространства

e1 6,9,1,0	T	,	e2 0,1,0,1	T	.

L1

:

Поскольку

R

4

, а ортогональная сумма есть прямая сумма,

L1 L1

dim L dim R4

dim L 4 2 2.

1

1

1

2

3

4

1

i

L

y

y , y

, y

, y

|

y,e

0, i

1,2 .

Таким образом,

L1 определяется системой уравнений

6y

9 y

2

y

3

0,

1

y4 0.

y2

Найдя фундаментальную систему решений этой однородной системы уравне-

ний, получим базис
	L1 .

	6	9	1				9	1
				0		6
	0	1	0		~		1	0
				1	0

0 1

.

y3	, y4		- свободные переменные;
y2 y4 ;
y1		1		9 y2	y3	1	y3	9 y4	.
		6				6
									1	y3
Общее решение имеет вид:
									6

3

2

									T
y		, y		, y		, y
	4		4		3		4

.

Выбирая значения свободных переменных в соответствии с таблицей

	i	i	i
		y3	y4
	1	6	0
	2	0	2

получаем базис ортогонального дополнения L1 :

					T ,
f	1		1,0,6,0

f2

3, 2,0,2	T

.

Пример 3. Найдите ортогональную проекцию

g

и перпендикуляр h , опу-

щенный из вектора	x 7, 4, 1,2 на подпространство
рами y1 0, 11,,0	и y2 5,7,0,1 .

L1

, порожденное векто-

Решение. Система векторов y1 , g L1 , 1 , 2 такие, что g 1 y1

единственное) представление x g

y2 образует базис подпространства L1 . Т.к.
2 y2 . Кроме того,	справедливо (причем
	. Последнее означает,
h , в котором h L1

что h, yi 0,

i 1,2

. Отсюда

x g, y

x y

2

y

2

, y

x, y

y

, y

2

y

2

, y

i

1 1

i

i

1

1

i

i

т.е. получили неоднородную систему уравнений относительно

рая в матричном виде выглядит так:

0,	i
	1

1,2, и 2

, кото-

y		, y			y		, y	2	x, y
	1		1			1				1		.
	y	, y			y		, y		x, y
			2			2		2		2
	1

Поскольку

5.3.3

y1 , y1 0 1 1 0 2;

y1 , y2 0 7 0 0 7;

x, y1 0 4 1 0 3;

y2 , y2 25 49 0 1 75;

x, y2 35 28 0 2 61,

система

5.3.3

эквивалентна следующей:

2		7 3	2		7	3
	7		~			.
		75 61		0	101 101

Отсюда

2 101101 1;

	1	1	3 7 3	3 7	2.
		2		2

Следовательно,

g 2 y	y																0
				2	2 0, 11,,0						5,7,0,1							5,2 7, 2 0,0 1		5, 5, 2, 1 ;
1
h x g			7, 4, 1,2
								5, 5, 2, 1						2,11,,3 .

5.3.1. Докажите, что ортогональное дополнение к странству евклидова пространства L обладает свойствами

линейному подпро-

:

L1;

б) если L1

L2 , то

а) L1

L2

L1 ;

в)

L L

0

L.

L

L ;

г) L 0,

1

2

1

2

Здесь 0- нулевое подпространство, содержащее лишь нулевой вектор.

5.3.2. Найдите базис ортогонального дополнения

линейной оболочки

L

L

следующей системы векторов пространства R

4

:

x

1,3,0,2

, x

2

3,7, 1,2 , x

3

2,4, 1,0 .

1

5.3.3. Найдите ортогональный базис ортогонального дополнения

L

, если

1	2		3	1				2				3
L L x , x		, x		и x		1,0,2,1 , x					2,1,2,3 , x				0,1, 2,1 .
5.3.4. В пространстве							Mn R многочленов степени n

коэффициентами скалярное произведение многочленов

с действительными

					t		t n
f	t			0
					1	n

и

				t		t n
g t			0
				1	n

определяется формулой

f , g	0
0

			n
1 1	n

.

5.3.4

Найдите ортогональное дополнение подпространства всех многочленов, удо-

влетворяющих условию f 1 0.

5.3.5. Найдите ортогональную проекцию и перпендикуляр, опущенный из вектора x на подпространство L1 :

а)

б)

x

x

14, 3, 6, 7 , L натянуто на векторы

2, 5,3,4 , L натянуто на векторы y1

y1 3,0,7,6 , y2 1,4,3,2

				2,2, 2, 2
y	3								;
1,3,3,5 ,					y	2			1,3, 5, 3 ,

y3 1, 5,3, 3 ;

в) x
		3,0, 5,9 ,
3	1	2		2			3
		4			3
5	1			2
	2			3
			2				3
1
г) x
	5,2, 2,2					, L

L задано системой уравнений:

2	4	0,

32 4 0,

10 4 0;

натянуто на векторы

y1 2,11,, 1 ,

y2 11,,3,0 ,

y

3

1,2,8,1 .

§ 5.4. Унитарное пространство

Говорят, что в комплексном линейном пространстве

L определено ска-

лярное произведение, если каждой паре векторов

x, y L

поставлено в соот-

ветствие комплексное число, обозначаемое

x, y

, причем это соответствие

удовлетворяет следующим аксиомам:

0

. x, y y, x

x, y L;

1

2

0

. x, y x, y

x, y L, C;

0

. x y, z x, z y, z

x, y, z L;

3

4

0

. x, x 0 при

x и x, x 0 при x .

Черта в первой аксиоме означает комплексное сопряжение.

Комплексное линейное пространство, в котором определено скалярное

произведение векторов, называется унитарным пространством.

Для любых двух векторов x и			y	унитарного пространства справедливо
неравенство КошиБуняковского:
x, y	2	x, x y, y .		5.4.1

В унитарном пространстве, как и в евклидовом, длину вектора определяют

формулой

x

x, x

.

5.4.2

Понятие угла между векторами в унитарном пространстве ривают лишь случай ортогональности векторов. При этом,

пространстве, ортогональными считают векторы x и y

не вводят. Рассмат-

как и в евклидовом

, удовлетворяющие

условию

x, y 0.

Процесс ортогонализации системы векторов, понятие ортогонального и ортонормированного базиса, ортогонального дополнения, ортогональной про-

екции вектора на подпространство и вообще вся теория евклидова простран-

ства распространяется на унитарное пространство без изменения определений и общих схем рассуждений. Тем не менее каждый раз следует быть вниматель-

ным при применении скалярного произведения, поскольку в унитарном про-

странстве скалярное произведение существенно отличается от скалярного про-

изведения в евклидовом пространстве.

Если

e1

,e2 , ,en - ортонормированный базис

n - мерного унитарного про-

странства

L

и для векторов x, y L имеют место разложения

x e

e

n

e ,

y e

2

e

n

e

,

1 1

2 2

n

1 1

2

n

то справедливы равенства:

x, y 1 1 2 2 n n ;

x, x 1 2 2 2 n 2 ;

i

x,ei , i

y,ei ,

i 1,2, ,n.

Пример 1. Ортонормируйте систему векторов

x

1,i,i ,

x

2

i,i,i ,

x

3

i,0,i

,

1

считая, что векторы заданы координатами в ортонормированном базисе.

Решение. Сначала проведем процесс ортогонализации данной системы

векторов. Положим y1 x1

1,i,i ,

y2 x2 21y1

и найдем 21

из условия

y

2

, y

x

2

21

y , y

21

y

, y

x

2

, y 0.

1

1

1

1

1

1

Получим

x2 , y1

i

1 i i i i

2 i .

21

y1

, y1

12 i 2 i 2

3

Поэтому

y			i,i,i		2 i	1,i
	2				3

Теперь положим

вий:

,i
y	3

2 2i				,		1
		3
x	3		31		y
						1

i 1 i

3 3

32 y2

.
и

31	,	32

будем искать из усло-

y3 , y1 31 y1, y1 x3 , y1 0;

y3 , y2 32 y2 , y2 x3 , y2 0.

Отсюда получаем:

					3				1					i 1 0 i i i								1 i
				x			, y																			;
	31		y				, y								3									3
					1				1
			x											i		2 2i					i			1 i
						3		, y		2									3					3								3 i
																																			.
	32		y2 , y2															2					2						2
														2 2i						1	i				1		i					4
														3							3						3
Поэтому
y3 i,0,i									1 i					1,i,i			3 i				2 2i							1 i				1 i
																											,				,
													3						4					3					3
																																3

	i		i
0,		,		.
	2 2

Система векторов

этой системы:

y	, y	2	, y	3
1

ортогональная. Нормируем каждый вектор

z			1		y				y					y							1	y		1	1,i,i ;
									1					1
1			y		1				y , y				2		2			2			3	1		3
			1						1	1		1		i		i
z			1		y				y	2									y	2							3	y
	2		y2			2			y2	, y2			2 2i				2		1 i			2	1 i		2		2		2
														3							3			3
			1		2 2i,1 i,1 i ;
			2	3

z

1

y

y

3

y

3

2 y

1

0,i,i .

3

y3

3

y3 , y3

3

i

2

i

2

2

2

2

Пример 2. Докажите, что векторы

x

и

y

унитарного пространства орто-

гональны тогда и только тогда, когда

x y

2

x

2

y

2

для любых чисел

и

.

Доказательство. Необходимость. Пусть

x, y 0. Тогда

x y 2

x y,x y

x, x

x,y

y, x

y,y

x 2 x, y y, x y 2

x 2 0 0 y 2 x 2 y 2 .

Достаточность. Пусть

x y

2

x

2

y

2

. Тогда из записанного выше

следует, что

x, y y, x x, y x, y 2 Re x, y 0

или

Re

x, y

0 , C.

Положим в последнем равенстве

1

.

Тогда

Re	x, y

Re x, y

0

.

Пусть теперь			1,	i . Тогда Re x, y Re i x, y Im x, y 0 . Следо-
вательно,		x, y 0.
	5.4.1. Докажите, что из аксиом скалярного произведения в унитарном про-
странстве вытекают следующие свойства:
а) x, y1 y2 x, y1 x, y2 для любых векторов унитарного пространства;
б) x, y x, y для любых векторов x, y								унитарного пространства и любого
	комплексного числа				;
в) , x x, 0;
	k	l		k	l
г)	i xi ,		j y j	i j xi , y j .
i 1		j 1		i 1 j 1

5.4.2. Докажите, что в любом комплексном линейном пространстве можно

определить скалярное произведение.

5.4.3. Введите скалярное произведение в n - мерном комплексном арифме-

тическом пространстве Cn .

5.4.4. Введите скалярное произведение в пространстве Mn C многочле-

нов с комплексными коэффициентами степени n .

5.4.5. Докажите, что в произвольном унитарном пространстве остается

справедливой

теорема

Пифагора: если векторы

x

и

y ортогональны, то

x y

2

x

2

y

2

. Покажите вместе с тем, что обратное к теореме Пифагора

утверждение неверно.

5.4.6. Докажите, что утверждение задачи 5.2.5.

x y

2

x y

2

2 x

2

2 y

2

справедливо и в унитарном пространстве.

5.4.7. Докажите равенство:

x y 2

x y 2 i x iy 2 i x iy 2 .

4 x, y

5.4.8.

Пусть

a 1,0,i , b 11, i,1 i , c 2 i,1,3 4i . Найдите длины

этих векторов и скалярные произведения a,b , b,c и

c,b считая, что векто-

ры a,b,c

заданы координатами в ортонормированном базисе.

5.4.9. Убедитесь, что система векторов x1 4 3i,4 3i,2 ,

x2

4 3i,4 3i,0

- ортогональная и дополните ее до ортогонального базиса

трехмерного унитарного пространства, считая, что векторы	x1 , x2	заданы ко-
ординатами в ортонормированном базисе.