Конспект_лекций_по_курсу_Дискретная_математика

Так как функция sin x определена на всей числовой оси, то областью опреде-

ления первого соответствия Q является все множество Х (Пр1Q = R). Так как синус принимает значения только в диапазоне от 1 до +1, то областью значений перво-

го соответствия будет замкнутый отрезок [ 1;1] (Пр2Q = [ 1;1]).

Так как логарифмы определены только	для положительных чисел, то
Пр1P 0; . В области определения логарифмы могут принимать любые вещест-
венные значения (при y 0 ln y ; при	y ln y ), следовательно,

Пр2Р = R.

Функция ln (sin x) определена для тех значений x, при которых sin x > 0, т.е.

Пр1S = {x| sin x > 0}. При этом логарифм может принимать значения от (при x 0) до 0 (при sin x = 1). Таким образом, Пр2S = ] ,0].

Из последнего примера видно, что область определения композиции может не совпадать с областью определения первого соответствия, а область значений ком-

позиции может не совпадать с областью значений второго соответствия.

Если множества X, Y и Z, для которых определены соответствия, конечны, то операцию композиции можно выполнить графическим или матричным способом.

Для графического выполнения композиции оба соответствия изображают на одном чертеже, совместив область прибытия первого соответствия с областью от-

правления второго соответствия. На графическом изображении композиции стрелками соединяют те и только те точки x X и z Z, которые на совмещенном чертеже исходных соответствий соединены хотя бы одним путем, идущим из x в z.

Пример 1.4.7. Выполним композицию соответствий P и Q, представленных на рис. 1.9, графическим способом

-21-

.

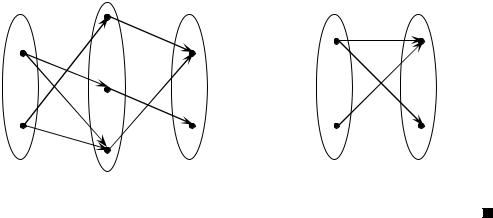
Q	P		S Q P
	y1
x1		z1	x1	z1
	y2
x2		z2	x2	z2
	y3
X	Y	Z	X	Z

Рис. 1.9

Для нахождения композиции соответствий с помощью матриц введем поня-

тие максиминного произведения матриц. Максиминное произведение матриц находится аналогично обычному произведению матриц, но вместо умножения элементов матриц используется операция выбора минимального из двух элемен-

тов, а вместо суммирования произведений соответствующих элементов выполня-

ется операция выбора максимального из минимальных элементов. Для вычисления элемента sij, стоящего на пересечении i-ой строки и j-го столбца результирующей матрицы, нужно взять i-ую строку первой матрицы и умножить ее максиминно на

j-ый столбец второй матрицы, используя формулу

sij	max min(qik , pkj ) ,	(1.2)
	k

где qik – элемент, стоящий на пересечении i-ой строки и k-го столбца первой мат-

рицы, а pkj – элемент, стоящий на пересечении k-ой строки и j-го столбца второй матрицы.

Если матрицы состоят, как в нашем случае, только из нулей и единиц, то максиминное произведение называют булевым (по имени известного английского математика, одного из основателей математической логики Джорджа Буля). В

этом случае формула (1.2) упрощается, так как если сомножители могут быть только нулями и единицами, то, как легко убедиться, минимальный из них равен их произведению, и формула (1.2) получает вид

sij	max qik pkj	(1.3)
	k

-22-

Из формул (1.2) и (1.3) следует, что sij = 1 тогда и только тогда, когда в i-ой строке первой матрицы имеется хотя бы одна единица, стоящая в этой строке на том же месте (k), что и единица в столбце второй матрицы. Сопоставление этого результата с определением композиции соответствий показывает, что если пере-

множаемые матрицы описывают некоторые соответствия, то их булево произведе-

ние описывает композицию этих соответствий.

Пример 1.4.8. Найдем матричным способом композицию соответствий из

примера 1.4.7.

0	1	1	1	0	1	1
M (Q)	0	;	M (P) 0	1 ;	M (Q P)
1		1	1	0	1	0

Элемент s11, стоящий на пересечении первой строки и первого столбца мат-

рицы M (Q P) , получается перемножением соответствующих элементов первой строки матрицы M(Q) и первого столбца матрицы M(Р), после чего из полученных произведений выбирается максимальное: s11 = max (0 1, 1 0, 1 1) = 1. Остальные элементы вычисляются аналогично.

Сопоставление матрицы M (Q P) с графическим изображением компози-

ции Q P на чертеже из примера 1.4.7 показывает, что, как и следовало ожидать,

результат получается одинаковым. 1.4.4. Отображения

Пусть задано соответствие <X, Y, Г>, где Г X Y.

Это соответствие называется отображением множества Х, если область опре-

деления этого соответствия совпадает с областью отправления, т.е. Пр1Г = Х.

Если при этом область значений соответствия совпадает с областью прибытия

(Пр2Г = Y), то говорят, что имеет место отображение множества Х на Y, если же область значений не совпадает с Y (Пр2Г Y), то имеет место отображение Х в Y.

Множество вторых элементов пар, входящих в отображение Г, в которых первым элементом является х, называется образом элемента х и обозначается Гх.

Очевидно, что Гх Y. Если элемент y Гх, то х называется прообразом элемента y.

-23-

Пример 1.4.9. 1. Пусть Х – множество преподавателей университета, Y –

множество учебных групп и пусть Г = {(x, y)| преподаватель х ведет занятия в группе y}. Так как все преподаватели ведут учебные занятия, то область определе-

ния этого соответствия совпадает с областью отправления Х, следовательно, соот-

ветствие Г является отображением. Так как занятия ведутся в каждой учебной группе, то область значений этого отображения совпадает с областью прибытия, и

Гесть отображение множества преподавателей Х на множество учебных групп Y.

2.Пусть X = Y = R – множество вещественных чисел и Г = {(x, y) | y = cos x}.

Так как косинус определен для любого вещественного числа, то Г является ото-

бражением множества вещественных чисел. Так как косинус принимает не любые значения, а только значения в диапазоне от 1 до +1, то Г есть отображение мно-

жества вещественных чисел в себя.

Частным видом отображения является функция. Отображение называется функцией, если каждый элемент области определения отображается ровно в один элемент области значений.

Пример 1.4.10. 1. В отображении Г = {(x, y)| y = cos x} из предыдущего при-

мера для каждого значения х существует только одно значение косинуса, следова-

тельно, это отображение является функцией, а отображение множества преподава-

телей на множество учебных групп функцией не является, так как преподаватель может вести занятия в нескольких группах.

2. Пусть X = Y = R – множество вещественных чисел, Г = {(x, y)| y = tg x}. Это соответствие не является отображением, так как тангенс определен не для любых вещественных чисел (например, tg ( /2) = ), следовательно, с точки зрения вве-

денных определений он не является и функцией. Однако, это утверждение спра-

ведливо только при принятом определении области отправления (Х = R). Если же принять, что Х = ] /2,+ /2 [, а Y = R, то тангенс будет функцией, отображающей

Хна Y.

3.Пусть соответствие q = <X, Y, Q> задано матрицей

-24-

0	1	0	0
M (Q) 1	0	0	0
0	0	0	1

Так как в каждой строке этой матрицы имеются единицы, то каждому элементу множества Х соответствует хотя бы один элемент множества Y и, следовательно,

это соответствие является отображением, причем это отображение Х в Y (ответьте,

почему). Так единиц в каждой строке имеется ровно по одной, то это отображение является функцией.

Ответьте, является ли функцией обратное соответствие Q 1?

1.4.5. Отношения

1.4.5.1. Определение

Отношением называется соответствие, в котором область отправления сов-

падает с областью прибытия.

Пусть <X, Y, R> соответствие, в котором X = Y, то есть это отношение. Так как области отправления и прибытия совпадают, то в описании отношения доста-

точно указать только одно из этих множеств. Таким образом, отношение пред-

ставляет собой пару <X, R>, где R Х Х.

Такое отношение называют бинарным отношением на множестве Х.

Оно состоит из множества пар (xi, xj), в которых xi Х и xj Х.

Понятие отношения можно распространить и на случай декартова произведе-

ния большего числа множеств Х Х ... Х, т.е. считать, что в паре <X, R>

R Х Х ... Х. Если декартово произведение содержит n сомножителей, то отно-

шение называют n-арным. Оно состоит из упорядоченных наборов (кортежей) по n

элементов, каждый из которых принадлежит множеству Х:

R {(x1, x2 ,...,xn ) | xi X ,i 1,n .

Например, операция сложения на множестве вещественных чисел a + b = c

может рассматриваться как тернарное отношение на этом множестве (тернарное

означает, что декартово произведение содержит три сомножителя):

-25-

R = {(a, b, c)| a, b, c E, c = a + b},

где E - множество вещественных чисел.

Далее мы будем рассматривать только бинарные отношения. При этом тот факт, что (x, y) R, будем обычно записывать xRy (читается: х находится в отно-

шении R к y).

Пример 1.4.11. 1. Пусть Х – множество людей. Будем считать, что xRy озна-

чает, что "х является братом y". Тогда R = {(x, y) | х, y Х, х – брат y} есть отноше-

ние на множестве людей.

2. Пусть Х - множество вещественных чисел. Будем считать, что xRy означает,

что число x является тангенсом числа y. Тогда R = {(x, y) | х, y Х, х = tg y} есть отношение на множестве вещественных чисел.

3. Пусть Х = {1, 2, 3, 4, 5, 6}. Будем считать, что xRy означает, что число x яв-

ляется делителем числа y. Тогда R = {( x, y) | х, y Х, х – делитель y} есть отноше-

ние на заданном подмножестве множества целых чисел.

1.4.5.2. Задание отношений Так как отношение – это частный случай соответствия, то для него действи-

тельны все известные способы задания соответствий, в частности графический и матричный. Но так как области отправления и прибытия здесь совпадают, то име-

ются некоторые особенности. Например, при матричном способе задания матрица всегда получается квадратной. При графическом способе задания области отправ-

ления и прибытия изображаются одним множеством точек.

Пример 1.4.12. Рассмотрим отношение делимости из предыдущего примера.

Матрица этого отношения имеет вид:

1	1	1	1	1	1
0	1	0	1	0	1
0	0	1	0	0	1
M (R) 0 0 0 1				0	0
0	0	0	0	1	0
0	0	0	0	0	1

-26-

Графическое представление показано на рис. 1.10:

2

3

1 4

6

5

Рис. 1.10

Так как каждое число делится на себя, то это изображается петлей в соответ-

ствующей точке (на петле стрелку можно не ставить).

1.4.5.3. Операции над отношениями Так как отношение является частным случаем соответствия, то все операции,

которые выполняются над соответствиями, могут выполняться и над отношения-

ми. При этом, естественно, нужно учитывать особенности определения и задания отношений. Так, композиция возможна только для отношений, заданных на одном и том же множестве. Если композиция выполняется графически, то оба отношения изображаются на одном и том же множестве элементов (точек), причем стрелки,

относящиеся к разным отношениям, обозначаются по-разному (например, для первого отношения – сплошными линиями, для второго – пунктирными). В ком-

позицию включаются такие пары элементов, которые соединены путями из двух стрелок, первая из которых принадлежит первому отношению, а вторая – второму.

Пример 1.4.13. Найдем графически композицию отношений P и Q, заданных на множестве X = {1, 2, 3, 4} (рис. 1.11).

1	2	1	2
4	3		3

Рис. 1.11

Совместим изображения отношений P и Q, изобразив стрелки отношения Q

пунктиром, и найдем в полученном совмещенном чертеже все пути, состоящие из двух стрелок, первая из которых сплошная, а вторая пунктирная (рис. 1.12). На но-

-27-

ˆ 2 n 2 n

M (R) M (R) M (R ) ... M (R ) ... M (R) M (R) ... M (R) ...

вом чертеже (рис. 1.13) изобразим точками то же множество самое множество X и

соединим в нем стрелками начала и концы найденных на предыдущем шаге путей.

В результате получим графическое представление композиции отношений P и Q.

1	2	1	2
4	3	4	3
Рис. 1.12			Рис. 1.13
Кроме того, имеется специфическая для отношений операция, называемая
транзитивным замыканием.

Если R – отношение на множестве Х: R Х Х, то его транзитивное замыка-

ние, обозначаемое		ˆ
		R , представляет собой отношение, задаваемое на том же мно-
жестве Х, т.е.	ˆ		ˆ	тогда и только тогда, когда существует
	R X X , и пара		(x, y) R

цепочка элементов z0 = x, z1, ..., zn = y, такая, что (zi 1, zi ) R, i 1,n , т.е. любая пара идущих друг за другом элементов этой цепочки входит в состав отношения R.

Свойства транзитивного замыкания:

1)	ˆ		ˆ
	Если (x, y) R, то (x, y) R , т.е. R R .
2)	ˆ			xRy xR Ry xR R Ry ... ( чита-
	(x, y) R тогда и только тогда, когда
	ˆ	2	R		3	... R	n	..., где R	n	R R ... R ,
ется "или"), откуда следует, что R R R

n

т.е. транзитивное замыкание отношения R есть объединение всех степеней этого отношения, где под n-ой степенью отношения понимается композиция этого от-

ношения с самим собой, выполненная n раз. Переходя к матрице, получим

(1.4)

В формуле (1.4) при вычислении матрицы композиции отношений использу-

ется булево произведение матриц, а объединение матриц отношений M(Q) = ||qij|| и

M(S) = ||sij||, заданных на одном и том же множестве, производится по формуле

tij = max (qij, sij),

(1.5)

-28-

где tij – элемент матрицы объединения отношений M (Q S) , стоящий на пересе-

чении i-ой строки и j-го столбца.

Для нахождения транзитивного замыкания графическим методом строится графическое представление отношения; на нем ищутся всевозможные пути произ-

вольной длины; в транзитивное замыкание включаются все те и только те пары элементов множества, первый из которых является началом пути, а второй его

концом.

Пример 1.4.14. 1. Пусть Х – множество людей. Определим отношение R сле-

дующим образом: R = {(x, y) | x – ребенок y)}, тогда транзитивным замыканием

			ˆ	= {(x, y) | x – потомок y)}.
этого отношения будет R
2. Пусть Х = {x1, x2, x3, x4, x5}, а отношение R задано графически (рис. 1.14).
Транзитивное замыкание этого отношения представлено на рис. 1.15.
		R						ˆ
			x2					R	x2
x1				x3			x1		x3
	x5			x4				x5	x4
		Рис. 1.14							Рис. 1.15
3. Найдем транзитивное замыкание предыдущего отношения матричным спо-
собом:
0 1	0	0	0	0	0	1	0	0	0 0 0 1	0
0 0	1	0	0	0	0	0	1	0	0 0 0 0	0
M (R) 0 0	0	1	0 ; M 2 (R) 0		0	0	0	0 ; M	3 (R) 0 0 0 0	0 ;
0 0	0	0	0	0	0	0	0	0	0 0 0 0	0
0 1	1	0	0	0	0	1	1	0	0 1 1 1	0

-29-

			0	1	1	1	0
			0	0	1	1	0
M	4	ˆ		0	0	1		Нетрудно видеть, что последняя матрица со-
		(R) 0 ; M (R) 0					0 .
			0	0	0	0	0
			0	1	1	1	0

ответствует графическому представлению транзитивного замыкания на рис. 1.15.

4. Пусть Х = {1, 2, 3, 4, 5, 6} и R = {( x, y)| х – делитель y}. Транзитивное замы-

кание этого отношения совпадает с самим отношением (убедитесь в этом само-

стоятельно).

1.4.2.4. Свойства отношений Рассмотрим шесть свойств, которыми могут обладать отношения.

1) Рефлексивность

Отношение R на множестве Х называется рефлексивным, если х (х, х) R,

т.е. все пары, состоящие из одинаковых элементов, всегда входят в отношение.

В матрице рефлексивного отношения на главной диагонали всегда стоят только единицы. В графическом представлении рефлексивного отношения в каж-

дой точке, изображающей объект из множества Х, имеется петля.

Пример 1.4.15. 1. Пусть Х – множество людей; R = {(x, y) | x – знаком с y}. Так как можно считать, что каждый человек знаком сам с собой, то это отношение рефлексивно.

2. Пусть Х – множество натуральных чисел; R = {(x, y)| x – делитель y}. Так как каждое натуральное число является своим собственным делителем, то свойст-

во рефлексивности выполняется.

3. Пусть Х – множество треугольников; R = {(x, y) | х подобен y}. Так как каждый треугольник подобен сам себе, то это отношение рефлексивно.

2) Антирефлексивность

Отношение R на множестве Х называется антирефлексивным, если

-30-