ответы к билетам матан 1 семестр docx - 2010 / 46.Знакопеременные ряды. Относительная и условная сходимость

Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.

Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.

Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.

Теорема 2 (достаточный признак сходимости знакопеременных рядов). Пусть

u₁+u₂+…+u_n+…=         (20)

знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов

│u₁│+│ u₂│+…+│ u_n │+…= │ u_n │.           (21)

Тогда ряд (20) тоже сходится.

Доказательство. Рассмотрим вспомогательный ряд

(u₁+│u₁│)+(u₂+│u₂│)+…+(u_n+│u_n│)+…= (u_n+│u_n│).            (22)

Очевидно, 0≤ u_n+│u_n│≤2│u_n│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд 2│u_n│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.

Замечание.

Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.

Например, ряд  сходится по признаку Лейбница, а ряд  расходится (это гармонический ряд).

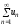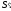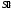Свойство 1. Если ряд абсолютно сходится, то он абсолютно сходится при любой перестановке его членов, при этом сумма ряда не зависит от их порядка; если − сумма всех его положительных членов, а − сумма всех абсолютных величин отрицательных членов, то сумма ряд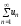а равна .

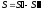Свойство 2. Если ряд 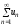абсолютно сходится и , то ряд также абсолютно сходится.

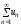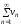Свойство 3. Если ряды и абсолютно сходятся, то ряды 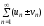также абсолютно сходятся.

Свойство 4. (теорема Римана). Если ряд условно сходится, то какое бы мы не взяли число А, можно так переставить члены данного ряда, чтобы его сумма оказалась в точности равной А; более того, можно так переставить члены условно сходящегося ряда, чтобы после этого он расходился.

2