Fundamentals of the Physics of Solids / 05-Symmetries of Crystals

5

Symmetries of Crystals

It has already been mentioned that crystalline materials constitute a highly important group of solids. In what follows, we shall be mostly concerned with the study of the properties of such materials. The reasons for this are not purely historical. On the one hand, crystalline materials are used in many applications. On the other hand, quite a few electronic properties do not depend on structure, and the theoretical study of the behavior of electrons within solids is much simpler in crystalline materials than in noncrystalline ones.

One of the most striking features of natural crystals is that they are usually bounded by regular plane faces. The regularity of the form – and thus the rotations and reflections that take the crystal into itself – are even better seen on artificially grown crystals.1 As R.-J. Haüy pointed out already in 1784, the regular form of carefully grown crystals implies that crystals are built up of regularly arranged small blocks. The regularity of the overall form is therefore the consequence of an internal regularity. It was well after Haüy’s time that atoms and ions were identified as the elementary building blocks, and it was shown that in the crystalline state atoms (or ions) with identical surroundings are arranged in a regular periodic array – implying that the crystal exhibits long-range order.

In the present chapter we shall discuss the geometrical characteristics of crystalline solids. Although atoms are not arranged in perfect order in real crystals – which may have important consequences on the properties of the solid –, here we shall assume that the crystal is ideal, i.e., perfectly regular and without defects. The various types of defects will be presented in Chapter 9. Noncrystalline solid structures will be discussed in Chapter 10.

1Being highly malleable, the crystalline symmetry of metals is almost always disguised in finished products.

110 5 Symmetries of Crystals

5.1 Translational Symmetry in Crystals

The characteristic regularity of crystalline structures is usually formulated in terms of the invariance of the crystal under certain discrete translations. As we saw in Chapter 2, there exist mesomorphic phases in which the material possesses discrete translational symmetries along one or two directions only and continuous ones along the others. Below we shall consider solids which are taken into themselves only by discrete translations in all three spatial directions. To put it more rigorously: A solid is said to be crystalline if there exist three non-coplanar vectors a1, a2, and a3 such that for any three integers n1, n2, and n3 translation through the vector

tn = n1a1 + n2a2 + n3a3

(5.1.1)

takes the sample into itself – while this is not the case for linear combinations in which the coe cients are not all integers. The vectors ai appearing in the definition are called primitive translation vectors or primitive vectors, and are said to span or generate the lattice. This formulation of discrete translational symmetry is the mathematical definition of ideal crystals.

Mathematically speaking, these translations form a group, T3. For convenience, we shall frequently refer to two-dimensional crystals. These are planar arrangements that are translationally invariant in the two planar dimensions (under the elements of the group T2).

Invariance under discrete translations does not apply solely to the regular array of spatially localized atoms. It also implies that the charge density ρe(r) of delocalized electrons, as well as the internal degrees of freedom (e.g., spin density) must be left unaltered by a translation through tn. Consequently, for any local observable quantity F (r)

F (r) = F (r + tn)

(5.1.2)

must hold. For nonobservable quantities – such as electron wavefunctions – this invariance does not apply. As we shall later, when considered separately, localized atoms and the charge density of delocalized electrons may exhibit di erent translational symmetries. Then the true translational symmetries of the whole system are translations through those vectors tn that transform both the localized atoms and the charge density into themselves.

5.1.1 Translational Symmetry in Finite Crystals

Strictly speaking, the previous formulation is valid only for infinite crystals. Finite crystals obviously cannot be taken perfectly into themselves by translations. However, where the original and translated samples overlap, the atomic arrangements must be identical – with the possible exception of a few atomic layers near the surface. The previous statement can be reformulated to be valid for finite samples: A sample of finite extent is said to be crystalline if

5.1 Translational Symmetry in Crystals

111

it is built up of identical elementary blocks (atoms, molecules, or groups of atoms/molecules) whose positions are given by the vectors in (5.1.1), and the triplets of integers n1, n2, n3 form a compact region. Figure 5.1 shows such a finite crystalline structure built up of groups of five atoms.

Fig. 5.1. A finite crystalline structure: a finite regular three-dimensional array of identical groups of atoms

A similar situation is encountered in crystal-growth processes. First, a nucleus is formed at random, and then other atoms/molecules condense onto it in a regular pattern. This construction of the crystal implies that whichever atom (of position vector r) of the starting group of atoms is chosen, identical atoms (in equivalent surroundings) are found at all points

r = r + tn = r + n1a1 + n2a2 + n3a3 ,

(5.1.3)

where the coe cients ni are integers, just as in (5.1.1). In general, when r and r are related through (5.1.3), F (r ) = F (r) holds for the spatial distribution of electron density and any local observable physical quantity F (r) – with the possible exception of the vicinity of the surface. Thus for finite crystals the relation (5.1.2) is valid only for positions r and r + tn that are both inside the sample.

5.1.2 The Choice of Primitive Vectors

One usually faces the opposite problem as in the previous theoretical construction of crystals. Given some regular arrangement of the atoms, one needs to determine the primitive vectors a1, a2, and a3. The choice of these vectors is ambiguous: if a vector triplet a1, a2, a3 is found such that the crystal is invariant under the translations tn given in (5.1.1), then the same invariance holds for any other vector triplet a1, a2, a3 that is a linearly independent set

112 5 Symmetries of Crystals

of linear combinations of the previous one with integer coe cients. However, the new vector triplet is not necessarily primitive (even when the old one is): it does not necessarily satisfy the condition that all translation vectors should be given by integer coe cients.

A possible choice for the primitive vectors a1 and a2 and a new set a1, a2 are shown in Fig. 5.2 for a two-dimensional crystal. With either choice, translations through tn = n1a1 + n2a2 or tn = n1a1 + n2a2 take the lattice into itself: each point is moved to an equivalent one. It is immediately seen that the two choices are nevertheless inequivalent: when translations through integer nis only are allowed, the choice on the right does not cover all the points that are equivalent to r: a1 and a2 are thus not primitive vectors.

a2	a’
	2
a1	a’
	1

Fig. 5.2. A possible choice for the primitive vectors and a pair of new vectors obtained through their linear combination in a two-dimensional crystal

Therefore the requirement that the vectors a1, a2, a3 be primitive – in other words: that the translations tn obtained with triplets of integers n1, n2, n3 yield all points r = r + tn in the crystal that are equivalent to r – is tantamount to stipulating that the volume of the parallelepiped spanned by the non-coplanar vectors a1, a2, a3 be minimum.

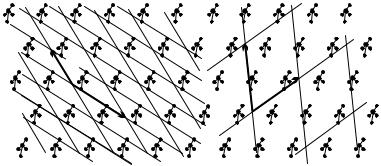
The minimum volume requirement is not perfectly restrictive either: it allows for many possible choices of the primitive vector, as shown in Fig. 5.3. For clarity, instead of the entire crystal only points that are equivalent to a selected one are marked.

Therefore it is useful to impose the restriction that the length of the vectors should be the smallest possible. Among the possible choices shown in Fig. 5.3 the leftmost meets this requirement. In many cases it is possible to go even further. Later, when the rotational symmetry of crystals will have been presented, it will be appreciated that primitive vectors should possibly be chosen in such a way that they are related through some symmetry operation. Moreover, in certain cases even the requirements of minimum volume and minimum length are abandoned so that rotational symmetry should be manifest. The lattice is then characterized by vectors a, b, and c that are

5.1 Translational Symmetry in Crystals

113

Fig. 5.3. Several possible choices for the pair of primitive vectors in a twodimensional crystal. In each case every equivalent point can be reached by a integer linear combination of the primitive vectors

more symmetric than the previously used primitive vectors a1, a2 and a3. Since a, b, and c are not primitive vectors, a part of the equivalent sites in the original lattice can be reached only via triplets of coe cients that contain nonintegers.

5.1.3 Bravais Lattice and Basis

Once the primitive vectors have been chosen and an origin selected, the endpoints of the vectors (5.1.1) marked for all possible integer values of n1, n2, and n3 make up a regular albeit empty lattice. This is called the point lattice or Bravais lattice of the crystal – named after the French crystallographer A. Bravais who was the first to determine correctly the possible lattice types in 1850. The points of a Bravais lattice are thus given by

Rn = n1a1 + n2a2 + n3a3 .

(5.1.4)

This will be important when we shall try to exploit the consequences of rotational symmetry.

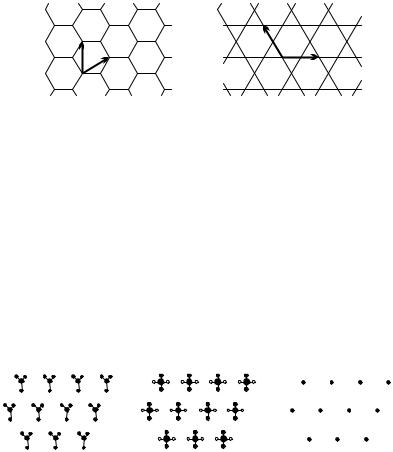
Note that the lattice concept introduced above is di erent from that used in statistical physics. Statistical physical models are often solved on honeycomb and kagome (basketweave)2 lattices (shown in Fig. 5.4). However, their vertices (sites) do not make up a lattice in the above sense. There are no primitive vectors whose linear combinations with integer coe cients give all the vertices and only the vertices. This is why when we present all possible types of planar lattices below these structures will not appear.

The knowledge of the primitive vectors, i.e., the point lattice is not sufficient for characterizing the crystal structure – even when only the spatial

2The name comes from the Japanese word kagome, meaning the pattern of holes (“me” = holes, literally “eyes”) in a woven (bamboo) basket (“kago”).

114 5 Symmetries of Crystals

(a)

(b)

Fig. 5.4. “Lattices” that are not Bravais lattices, and their primitive vectors: (a) honeycomb lattice; (b) kagome lattice

arrangement of atoms, i.e., the geometry of the crystal is considered. One must also identify the group of atoms whose regularly repeated pattern makes up the lattice. This group of atoms is called the basis or motif of the crystal. The honeycomb net and the kagome lattice are thus Bravais lattices with a twoand a three-point basis, respectively.

When the same Bravais lattice is decorated with di erent bases, di erent crystal structures are obtained. Conversely, crystals with strikingly di erent structure may share the same underlying Bravais lattice. It is easily seen that the two-dimensional crystals shown in parts (a) and (b) of Fig. 5.5 have di erent bases but a common Bravais lattice, which is shown in part (c). The crystal structure is therefore determined by its Bravais lattice and its basis.

(a)

(b)

(c)

Fig. 5.5. (a) and (b): Two-dimensional crystals that are built up of di erent groups of atoms but exhibit the same translational symmetries. (c): Their common Bravais lattice

When the basis consists of a single atom, then the origin of the coordinate system can always be chosen so that each atom should occupy a lattice site Rn. On the other hand, in crystals with a p-point basis the arrangement of the atoms in the basis should appear exactly the same around each lattice site; therefore atomic positions are given by the sum of a lattice vector Rn and a vector rμ (μ = 1, 2, . . . , p), which is referred to the corresponding lattice site, thus lies in the unit cell.

5.1.4 Primitive Cells, Wigner–Seitz Cells, and Bravais Cells

The basis is not always pictured as a group of several point-like atoms. It can also be thought of as an extended charge distribution. It is then not

5.1 Translational Symmetry in Crystals

115

just a collection of atoms but an elementary region with atoms (ions) and a smeared-out electron cloud. Such an elementary region called primitive unit cell or primitive cell contains exactly one lattice point. When it is repeated according to a regular spatial pattern, i.e., translated through all vectors tn, the volume of the crystal is covered in its entirety. This condition does not impose a strong restriction on the shape of the primitive cell. It does not need to possess high symmetry, nor are its faces required to be plane (or in the two-dimensional case: its sides to be straight). Complete filling of the space or complete tiling of the plane requires only that opposite faces (sides) could be moved into one another by simple translations – leaving considerable freedom in the choice of the figures. Beautiful examples for periodic tilings of the plane are found on embroideries, wall decorations, and mosaics. In his artistic program the Dutch artist M. C. Escher3 illustrated possible symmetries in the complete tiling of the plane using human and animal figures. Some of his works are shown in Fig. 5.6, as well as in Figs. 5.27 and 5.31 in the later parts of this chapter.

Fig. 5.6. Escher’s drawings show the complete tiling of the plane with human and animal figures

3 M. C. Escher, 1898–1972.

116 5 Symmetries of Crystals

It is a straightforward matter to prove that it is often impossible to fill the space or tile the plane with patterns of high symmetry. The plane cannot be perfectly tiled with identical circles, and space cannot be entirely filled with identical spheres. For mathematical simplicity, the electron states are nevertheless often determined within a sphere centered on a lattice site (the Wigner–Seitz sphere). This approximation and its problems will be discussed in Chapter 19 of Volume 2 where the study of electron states is presented.

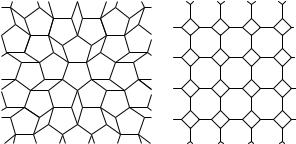
It should also be mentioned here – without going into the details of the geometrical problem of finding those solids bounded by plane faces that can fill up space perfectly – that perfect tilings of the plane are possible with regular or distorted triangles, quadrilaterals, or hexagons while the tiling will be imperfect when regular pentagons or octagons are used, as shown in Fig. 5.7. In the case of pentagons allowing for nonidentical orientation does not help either. It will be shown in Section 10.2 on quasicrystals that the plane can be tiled in such a manner that local fivefold symmetry is manifest – provided that the requirement of complete translational symmetry is relaxed and only that of quasiperiodicity is imposed.

Fig. 5.7. Incomplete tiling of the plane with regular pentagons and octagons

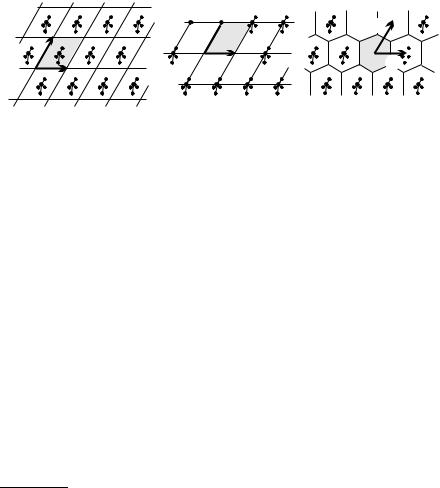
A common choice for the primitive cell is the parallelepiped spanned by the primitive vectors a1, a2, and a3. Clearly, a regular array of such parallelepipeds fills the space completely, without overlaps. Figure 5.8(a) shows the division of the two-dimensional periodic crystal structure of Fig. 5.2 into cells spanned by the minimum-length primitive vectors a1 and a2.

The freedom in the choice of the origin is customarily abandoned in favor of choosing a characteristic atom of the crystal as the starting point of the primitive vectors. In this construction the group of atoms around a particular lattice site is usually divided among several primitive cells. Another disadvantage of this choice for the primitive cell is that translational symmetry alone is taken into account: the internal structure and symmetries of the figure the crystal is built up of are completely ignored. That is why in many cases – in particular, when the electron states are to be determined – the crystal is divided into primitive cells in such a manner that in addition to the atoms,

5.1 Translational Symmetry in Crystals

117

the core electrons should also belong to the same region. Such a division is obtained through Dirichlet’s construction.

Consider the points of a crystal lattice. In Dirichlet’s construction one associates with each lattice point the region of space that is closer to that point than to any other lattice point. To construct these regions, vectors are drawn from the point in question to its first, second and perhaps third neighbors, and then perpendicular planes are drawn through the midpoint of each vector. The primitive cell obtained this way is called the Wigner–Seitz cell.4 Part (c) of Fig. 5.8 shows the tessellation of the two-dimensional crystal of parts (a) and (b) into Wigner–Seitz cells.

a2

a1

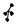a2a1

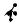
a2 a1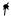

(a)

(b)

(c)

Fig. 5.8. Three di erent choices for the primitive cells (shaded areas) that allow for perfect tiling of the two-dimensional crystal. (a) and (b) di er only in the choice of the origin; (c) tessellation by Wigner–Seitz cells

It has been mentioned that the relative orientation of the primitive vectors does not necessarily reflect the crystal symmetries, which is why sometimes longer but more symmetric vectors, a, b, and c are used instead. As an example, consider the plane lattice shown in Fig. 5.9. The primitive vectors are of di erent lengths, and their angle is such that 2a2 − a1 is perpendicular to a1.

Instead of a1 and a2 one might choose the vectors a = a1 and b = 2a2 −a1. This choice gives a rectangular (nonprimitive) unit cell instead of the rhomboid-shaped primitive cell. Horizontal and vertical reflection symmetry

– which are the consequence of the particular relation between a1 and a2 (2a2 − a1 a1) as well as the appropriate choice of b – are manifest in this case. The parallelepiped spanned by these vectors is called the conventional unit cell or the Bravais cell of the crystal. The general definition of the Bravais cell will be given on page 144.

Since it may contain several crystallographically equivalent sites, the Bravais cell may have a larger volume than the primitive cell or the Wigner–Seitz cell. In the above example lattice points are found inside the rectangles as well

4E. Wigner and F. Seitz, 1933. When Dirichlet’s construction is applied to sets of discrete points that do not necessarily form a Bravais lattice, the obtained irregular units are known as Voronoi polyhedra (G. Voronoi, 1908).

118 5 Symmetries of Crystals

a a1

b	b 2a2 a1 a1

a2

a1

a

Fig. 5.9. The rhomboid-shaped primitive cell and the rectangular Bravais cell of a special oblique lattice

as at their vertices. The Bravais cell is thus not necessarily a primitive cell – it is nevertheless often a convenient choice because of its higher symmetry.

5.1.5 Crystallographic Positions, Directions, and Planes

As it was mentioned on page 114, the position vectors ri of the atoms of the basis are referred to the points of the Bravais lattice – and these vectors do not depend on the choice of the particular cell. The position vectors are customarily expressed in terms of the primitive vectors (which are generally not mutually orthogonal):

ri = xi1 a1 + xi2a2 + xi3 a3 ,

(5.1.5)

where the coordinates xi1, xi2, and xi3 range between 0 and 1 or −12 and 12 . The position vector is concisely denoted by the three coordinates xi1 xi2 xi3 . Thus 12 12 0 refers to the position given by the vector 12 a1 + 12 a2. Negative numbers are denoted by overlines, e.g., the concise notation for the point at

12 a1 − 14 a2 is 12 14 0.

A specified direction in the crystal is denoted by a triplet of integers in square brackets: [u v w] stands for the direction of the vector u a1 +v a2 +w a3. In a cubic lattice – made up of cubic primitive cells – [100], [110], and [111] denote the direction of an edge, a face diagonal, and a space diagonal. The directions of the three cube edges ([100], [010], [001]) and their opposites

¯ ¯ ¯

([100], [010], [001]) are obviously equivalent. They are collectively referred to as the 100 directions.

In what follows, coplanar atoms will be of particular importance. Consider any three noncollinear points of a Bravais lattice and their common plane. Translational symmetry of the lattice implies that there are an infinite number of lattice points on this plane – moreover the family of equidistant parallel planes contains all the lattice points. Figure 5.10 shows this for a twodimensional section of the lattice with three possible choices for the family of planes.

Crystal planes are also denoted by triplets of integers. To specify the three indices, consider the member of the family of planes that is closest to the plane