Quantum Chemistry of Solids / 21-Basis Sets and Pseudopotentials in Periodic LCAO Calculations

8

Basis Sets and Pseudopotentials in Periodic LCAO

Calculations

8.1 Basis Sets in the Electron-structure Calculations of

Crystals

8.1.1 Plane Waves and Atomic-like Basis Sets. Slater-type Functions

The choice of the basis set is of particular importance when treating periodic systems where a large variety of chemical bonding can be found. The following three approaches to the basis-set choice define three types of methods of the electronicstructure calculations in crystals [10]: atomic-sphere (AS) methods, plane-wave (PW) methods, localized atomic-like orbitals (LCAO) methods. Each method has its advantages and disadvantages.

The basic idea of AS methods is to divide the electronic-structure problem, providing e cient representation of atomic-like features that are rapidly varying near each nucleus and smoothly varying functions between atoms [10]. The smooth functions are augmented near each nucleus by solving the Schr¨odinger equation in the sphere at each energy and matching to the outer wave function. The resulting APW (augmented plane waves) or KKR (Kohn–Korringa–Rostoker) methods are powerful but require solution of nonlinear equations. The linear modifications of AS methods (LAPW, LMTO) use the familiar form of a secular equation involving a Hamiltonian and overlap matrix. The full-potential linear methods (FPLAPW) provide the most precise solutions of the Kohn–Sham equations.

The simpler PW methods are the most popular in the Kohn–Sham periodicsystems calculations. Plane waves are an orthonormal complete set; any function belonging to the class of continuous normalizable functions can be expanded with arbitrary precision in such a basis set. Using the Bloch theorem the single-electron wavefunction ϕi(r) can be written as a product of a wave-like part and a cell-periodic

part ϕik = exp(ikr)ui(r) (see Chap. 3). Due to its periodicity in a direct lattice ui(r)

can be expanded as a set of plane waves ui(r) = CiB exp(iBr), where B is the

B

reciprocal lattice vector. Thus, in the PW basis the single-electron wavefunction can be written as a linear combination of plane waves

ϕik(r) = CiB exp(i(k + B)r)	(8.1)

B

2

|k+B|2

282 8 Basis Sets and Pseudopotentials in Periodic LCAO Calculations

The number of basis functions used is controlled by the largest wavevector in the expansion (8.1). This is equivalent to imposing a cuto on the kinetic energy as the

kinetic energy of an electron with wavevector (k + B) is given by . Thus, the size of the PW basis set is defined by the so-called cuto energy, i.e. the kinetic energy for the largest reciprocal lattice vector included in the PW basis. The Kohn–Sham equations take on a very simple form using plane waves [377]

	1
(	2	|k + B|2δBB	+ VeN (B − B ) + Vee(B − B )
B
+VXC (B − B )) Ci,k+B = Ci,k+B εik				(8.2)

where VeN (B −B ), Vee(B −B ), and VXC (B −B ) are the Fourier transforms of the electronic–nuclei, electron–electron Coulomb, and exchange-correlation potentials.

The PW basis set is universal, in the sense that it does not depend on the positions of the atoms in the unit cell, nor on their nature [458]. One does not have to construct a new basis set for every atom in the periodic table nor modify them in di erent materials, as is the case with localized atomic-like functions and the basis can be made better (and more expensive) or worse (and cheaper) by varying a single parameter – the number of plane waves defined by the cuto energy value. This characteristic is particularly valuable in the molecular-dynamics calculations, where nuclear positions are constantly changing. It is relatively easy to compute forces on atoms. Finally, plane-wave calculations do not su er from the basis-set superposition error (BSSE) considered later. In practice, one must use a finite set of plane waves, and this in fact means that well-localized core electrons cannot be described in this manner. One must either augment the basis set with additional functions (as in linear combination of augmented plane waves scheme), or use pseudopotentials to describe the core states. Both AS and PW methods, developed in solid-state physics are used to solve Kohn– Sham equations. We refer the reader to recently published books for the detailed description of these methods [9–11].

In the quantum chemistry of solids the LCAO methods are preferable [458]. These methods are more flexible as they allow both Hartree–Fock and Kohn–Sham equations to be solved, are applicable in the correlated wavefunction approaches (post-Hartree– Fock methods, see Chap. 5) and in Kohn–Sham theory based on hybrid exchangecorrelation functionals (see Chap. 7). In comparison with plane waves, the use of allelectron LCAO calculations allows us to describe accurately electronic distributions both in the valence and the core region with a limited number of basis functions. The local nature of the basis allows a treatment both of finite systems and of systems with periodic boundary conditions in one, two or three dimensions. This has an advantage over plane-wave calculations of molecules, polymers or surfaces that work by imposing artificial periodicity: the calculation must be done on, e.g. a three-dimensional array of molecules with a su ciently large distance between them (the molecule is placed at the center of a periodic supercell). LCAO total energies can be made very precise (i.e. reliable to many places of decimals) since all integrals can be done analytically (in practice, this is only true for Hartree–Fock calculations; density-functional theory LCAO calculations require a numerical integration of the exchange-correlation potential that reduces the attainable precision). Having an “atomic-like” basis facili-

8.1 Basis Sets in the Electron-structure Calculations of Crystals

283

tates population analyses, the computation of properties such as projected densities of states, and “pre-SCF alteration of orbital occupation” making the convergence of SCF calculations faster. As was already noted the LCAO basis allows easy comparison of the results obtained for molecules and solids at the same precision level of calculations.

The molecular basis set atomic-like orbitals can be considered as a starting point to generate atomic basis sets to be used in crystalline compounds. Therefore, we begin with the molecular basis-sets description.

In molecular quantum chemistry two types of atomic-like basis sets are used: Slater-type orbitals (STO) and Gaussian-type orbitals (GTO). In fact, it is not really correct to call them “orbitals”. They are better described as basis-set functions, since they are Slater-type or Gaussian-type functions used to approximate the shapes of the orbitals defined as one-electron wavefunctions. Using the acronyms accepted in solid-state theory it would be possible even call LCAO methods for crystals to “allelectron or full potential linear combination of Slater (Gaussian)-type functions – FP LS(G)TF method” [458], compare with the acronym FP LAPW (full potential linear combination of augmented plane waves).

The mathematical form of the normalized primitive Slater-type function (STF) in atom-centered polar coordinates is

χnlmST F (r) = Nnl(ζ)rn−1 exp(−ζr)Ylm(θ, ϕ) = Rnl(r)Ylm(θ, ϕ)

(8.3)

where ζ is an orbital exponent, n is the principal quantum number, Ylm(θ, ϕ) are the spherical harmonics, depending on the angular momentum quantum numbers l and m. STF have a number of features that make them attractive, see Sect. 6.1.1. We note the di erence between Slater-type orbitals (8.3) and Slater orbitals introduced by Slater [210] and used in semiempirical LCAO methods, see Chap. 6. The radial part of the Slater orbitals Rnl(r) depends on two parameters: the e ective quantum number n and screening parameter constant s. The values of these parameters are given by the following rules:

(1)n is assigned by the following table, in terms of the real principal quantum number n: for n = 1, 2, 3, 4, 5, 6 – n = 1, 2, 3, 3.7, 4.0, 4.2.

(2)For determining (Z − s), the electrons are divided into the following groups, each having a di erent screening constant: 1s; 2s, 2p; 3s, 3p; 3d; 4s, 4p; 4d; 4f ; 5s, 5p; 5d; etc. That is, the s and p of a given n are grouped together but the d and f are separated. The shells are considered to be arranged from inside out in the order named.

(3)The screening constant s is formed, for any group of electrons, from the following contributions: (a) Nothing from any shell outside the one considered, (b) an amount 0.35 from each other electron in the group considered (except in the 1s group, where 0.30 is used instead).

(c) If the shell considered is an s, p shell,	an	amount	0.85	from	each	electron
with total quantum number less by one, and	an	amount	1.00	from	each	electron

still further in; but if the shell is a d or f , an amount 1.00 from every electron inside it. As an example, we take the carbon atom C, Z = 6. Here, we have two 1s electrons, four 2s, 2p electrons. For the e ective nuclear charge, Z − s, we have 1s : 6 − 0.30 = 5.70; 2s, p : 6 − 3(0.35) − 2(0.85) = 3.25. As a second example, we take the iron atom Fe, Z = 26. There are two 1s, eight (2s, p), eight (3s, p), six (3d), two (4s). The e ective nuclear charges are: 1s : 26 − 0.30 = 25.70; 2s, p :

284 8 Basis Sets and Pseudopotentials in Periodic LCAO Calculations

26 − 7(0.35) − 2(0.85) = 21.85; 3s, p : 26 − 7(0.35) − 8(0.85) − 2(1.00) = 14.75; 3d : 26 − 5(0.35) − 18(1.00) = 6.25; 4s : 26 − 1(0.35) − 14(0.85) − 10(1.00) = 3.75. These simple rules give approximate Slater analytic atomic wavefunctions for all the atoms and ions.

The Slater orbitals can be written in the form (8.3) with the orbital exponent

ζ = Z−s and n = n .

n

The Slater-type functions (STF) with the radial part in the form (8.3) and integer n can be used as the basis functions in Hartree–Fock–Roothaan calculations of atomic wavefunctions. The radial dependence of the atomic orbitals is an expansion in the radial Slater-type basis functions ϕlmp whose indices are l, running over s, p, d, f, . . .

symmetries, and p counting serially over basis-set members for a given symmetry:

ϕlmi = ClmpRlp(r)Ylm(θ, ϕ)	(8.4)
p

The radial expansion is independent of m; all electrons with a given l, i have the same radial dependence. The orbital angular dependence Ylm(θ, ϕ) is a normalized spherical harmonic. The expansion coe cients Clmp of the ith orbital, for the occupied atomic orbitals, are tabulated for elements with Z=1–54 in [65] and with Z=55–92 in [459]. Relatively few primitive STOs are needed to closely approximate HF solutions of atoms (the latter are known as the contracted Slater-type orbitals). For example, six s-functions and four p-functions are enough to give seven-figure accuracy in total energy for the ground states of the first-row atoms. In Table 8.1 we give the results of Hartree–Fock–Roothaan carbon atom ground-state calculations. The one-electron energies of occupied 1s, 2s and 2p AOs and the corresponding primitive STFs orbital exponents ζ and coe cients Clmp are shown. The STF basis set for the carbon atom can be denoted as 6s-6s4p, meaning that the core 1s AO is represented by six s- orbitals and the valence 2s- and 2p-orbitals are represented by six s- and four p- orbitals, respectively.

The Slater-type orbitals were the first to be used in the molecular quantum chemistry semiempirical calculations. Unfortunately, such functions are not suitable for fast calculations of multicenter integrals in ab-initio calculations. Gaussian-type functions (GTFs) were introduced to remedy the di culties. GTFs are used in basis sets in practically all modern codes for LCAO calculations of molecules. We know two exclusions

Table 8.1. HF SCF occupied atomic orbitals for the ground state of a carbon atom given as linear combinations of s and p STOs [65]. The one-electron energies are given in a.u.

s			1s : C	2s : C	p			2p : C
basis	ζ		–11.32554	–0.70563	basis	ζ		–0.43335
1s	5.43599		0.93262	–0.20814	2p	0.98073		0.28241
1s	9.48256		0.06931	–0.01071	2p	1.44361		0.54697
2s	1.05749		0.00083	0.08099	2p	2.60051		0.23195
2s	1.52427		–0.00176	0.75045	2p	6.51003		0.0.1025
2s	2.68435		0.00559	0.33549
2s	4.20096		0.00382	–0.14765

8.1 Basis Sets in the Electron-structure Calculations of Crystals

285

from this rule – KS LCAO codes SIESTA [344] and ADF [345]. The SIESTA code uses a numerical AO basis set, the ADF code uses Slater-type basis set orbitals (see Appendix C). In the next section we consider the GTF used in molecular quantum chemistry.

8.1.2 Molecular Basis Sets of Gaussian-type Functions

A primitive Gaussian-type function can be written in a local Cartesian coordinate system in the form

χGT F = xlymzn exp(−αr2)

(8.5)

where α is the orbital exponent, and the l, m, n are not quantum numbers but simply integral exponents of Cartesian coordinates. Gaussian primitives (8.5) can be factorized into their Cartesian components, i.e. χGT F = χGTx F χGTy F χGTz F , where each Cartesian component has the form (introducing an origin such that the Gaussian is located at position A),

χGTx F = (x − xA) exp −α(x − xA)2 (8.6)

This simplifies considerably the calculation of integrals. If we write the exponential

part of an STF, exp(−αr) in Cartesian components we get exp(−α		2	2		x2)
		x + y		+n 1
that is not so separable. Note that the absence of the STO pre-	exponential factor r				−
		4

restricts single Gaussian primitives to approximating only 1s, 2p, 3d etc. orbitals and not, e.g. 2s, 3p, 4d, etc. However, combinations of Gaussians are able to approximate correct nodal properties of atomic orbitals if the primitives are included with di erent signs. The sum of exponents of Cartesian coordinates L = l+m+n is used analogously to the angular-momentum quantum number for atoms to mark Gaussian primitives as s-type (L = 0), p-type (L = 1), d-type (L = 2), f -type (L = 3) etc. From six 3d GTFs (x2, xy, xz, yz, y2, z2) there are only five linearly independent and orthogonal atomic d- orbitals being linear combinations of Cartesian Gaussians (3z2 −r2, xz, yz, x2 −y2, xy), the sixth combination x2 + y2 + x2 = r2 is Gaussian primitive of s-type.

It is clear that the behavior of a Gaussian is qualitatively wrong both at the nuclei and in the long-distance limit for a Hamiltonian with point-charge nuclei and Coulomb interaction. From this point of view STFs would be preferable.

In so-called Pople basis sets, the basis functions are made to look more like Slatertype functions by representing each STF χST F as a linear combination of Gaussian primitives:

N
i		(8.7)
χST F = C χGT F
i	i
=1

where Ci is a fixed coe cient and N is the number of Gaussian primitives used to represent the Slater-type basis function. The sums (8.7) are known as the contracted Gaussian basis set. Linear combinations of Gaussian primitives allow the representation of the electron density close to the nucleus to be improved. Recall that STF has a cusp at the nucleus, while GTF does not. By taking linear combinations of Gaussian primitives, the cusplike behavior is better reproduced.

The Gaussian basis set can also be used without any connection with the Slatertype orbitals: HF equations solutions for atoms are reached by Roothaan’s expansion

286 8 Basis Sets and Pseudopotentials in Periodic LCAO Calculations

method with Gaussian-type functions as was done with STFs (see Sect. 8.1.1). The details of both procedures – Gaussian expansion of Slater-type orbitals and atomic SCF calculations with Gaussian-type basis – are well known in molecular quantum chemistry [460]. It was found that GTF expansions require inclusion of more primitives than STF expansions for the same accuracy in the total and one-electron SCF energies for atoms. For example, in the case of the carbon atom the inclusion of 10 s-type primitive GTFs and 6 p-type primitive GTFs is necessary (10s − 10s6p) to obtain only six-figure accuracy in the total energy (in the STF case seven-figure accuracy was obtained for 6 and 4 STF s-type and p-type primitives, respectively).

In molecular quntum chemistry Gaussian-type basis functions are expanded as a linear combination (contraction) of individually normalized Gaussian primitives gj (r) characterized by the same center and angular quantum numbers but with di erent exponents

N

χi(r) = dj gj (r), gj (r) = g(r; α, l, m) = Nlm(α)rlYlm(θ, φ) exp(−αj r2) (8.8)

j=1

where N is the length of the contraction, the αj are the contraction exponents, the dj are contraction coe cients. Gaussian primitives can be written in terms of real spherical harmonics including a normalization constant.

If accurate solutions for an atom are desired, they can be obtained to any desired accuracy in practice by expanding the “core” basis functions in a su ciently large number of Gaussians to ensure their correct behavior. Furthermore, properties related to the behavior of the wavefunction near nuclei can often be predicted correctly, even without an accurately “cusped” wavefunction [461]. In most molecular applications the asymptotic behavior of the density far from the nuclei is considered much more important than the nuclear cusp [458]. The molecular wavefunction for a bound state must fall o exponentially with distance, whenever the Hamiltonian contains Coulomb electrostatic interaction between particles. However, even though an STFs basis would, in principle, be capable of providing such a correct exponen-

tial decay, this occurs in practice only when the smallest exponent in the basis set

√

is ζmin = 2Imin, where Imin is the first ionization potential. Such a restriction on the range of exponent values, while acceptable for atomic SCF calculations, is far too restrictive for molecular and solid-state work. Some of these formal limitations have thus turned out to be of relatively little importance in practice.

By proper choice of the N , αj , and dj in the contraction (8.8) the “contracted Gaussians” may be made to assume any functional form consistent with the primitive functions used. One may therefore choose the exponents of the primitives and the contraction coe cients so as to lead to basis functions with desired properties, such as reasonable cusp-like behavior at the nucleus (e.g. approximate Slater functions or HF atomic orbitals). Integrals involving such basis functions reduce to sums of integrals involving the Gaussian primitives. Even though many primitive integrals may need to be calculated for each basis function integral, the basis function integrals will be rapidly calculated provided the method of calculating primitive integrals is fast, and the number of orbital coe cients in the wavefunction will have been considerably reduced. The exponents and contraction coe cients are normally chosen on the basis of relatively cheap atomic SCF calculations so as to give basis functions suitable for

8.1 Basis Sets in the Electron-structure Calculations of Crystals

287

describing exact Hartree–Fock atomic orbitals. An approximate atomic basis function, whose shape is suitable for physical and chemical reasons, is thus expanded in a set of primitive Gaussians, whose mathematical properties are attractive from a computational point of view. Note that the physical motivation for this procedure is that, while many primitive Gaussian functions may be required to provide an acceptable representation of an atomic orbital, the relative weights of many of these primitives are almost unchanged when the atoms are formed into molecules or crystals. The relative weights of the primitives can therefore be fixed from a previous calculation and only the overall scale factor for this contracted Gaussian function need be determined in the extended calculation. It is clear that contraction will in general significantly reduce the number of basis functions.

For molecular basis sets of Gaussian-type functions (GTF) general acronyms and notations are used that are well known in molecular quantum chemistry.

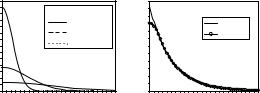
A Minimal-basis sets are constructed by using one Slater-type orbital basis function of each type occupied in the separated atoms that comprise a molecule. If at least one p-type, d-type or f -type orbital is occupied in the atom, then the complete set (3 p-type, 5 d-type, 7 f -type) of functions must be included in the basis set. The simplest of these basis sets is that designated STO-3G, an acronym for Slater-type-orbitals simulated by 3 primitive Gaussians added together. The coe cients of the Gaussian functions are adjusted to give as good a fit as possible to the Slater orbitals. To illustrate this, let us consider a 1s Slater-type orbital radial part exp(−ζr) (for ζ = 1.0 it is an exact hydrogen atom atomic orbital). A plot of this STO function is given in Fig. 8.1b, taken from [458]. A plot of Gauusian-type orbitals exp(−ζr2) for di erent orbital exponents is shown in Fig. 8.1a. Note the cusp at the origin for the Slater-type orbital while the Gaussian-type orbital has no cusp at the origin. In addition, the shape of the Gaussian-type orbital is di erent due to the squared distance that appears in its exponent. In Fig. 8.1a are shown individually three 1s-Gaussian primitives with orbital exponents 0.1098, 0.4058 and 2.2277. When the Gaussian primitives are combined using the coe cients 0.4446, 0.5353 and 0.1543, a new STO-3G function is produced, which is shown in Fig. 8.1b. It is seen that the new basis function resembles the Slater-type orbital much more closely than any of the single Gaussian-type orbitals. The only slight variation is observed near the cusp. The new basis function, because it consists of Gaussian primitive functions, does not have a cusp. However, the overall shape even close to the nucleus is very much like the Slater-type orbital.

)r ( 1s R

a

1.4

1.2Gaussians:

α= 0.1098

α = 0.4058

0.8α = 2.22771.0

0.6

0.4

0.2

0.0

0 1 2r, a.u.3 4

		b
	0.6
	0.5				Slater
	0.4
)					STO-3G
(r	0.3
s
1
R	0.2
	0.1
5	0.0 0	1	2	3	4	5
			r, a.u.

Fig. 8.1. 1s orbitals, [458]: (a) Gaussian; (b) Slater and fitted STO-3G

288 8 Basis Sets and Pseudopotentials in Periodic LCAO Calculations

Only one best fit to a given type of Slater orbital is possible for a given number of Gaussian functions. Hence, all STO-3G basis sets for any row of the periodic table are the same, except for the exponents of the Gaussian functions. The exponents are expressed as scale factors, the squares of which are used as multipliers of the adjusted exponents in the original best-fit Gaussian functions. In this way, the ratios of exponents remain the same while the e ective exponent of each orbital can be varied, [458]. The STO-3G basis set, and other minimal basis sets, usually do reasonably well at reproducing geometries of only simple organic molecules. The minimal basis sets do not allow alteration of the basis orbitals in response to a changing molecular environment and therefore make comparison between charged and uncharged species unreliable. Anisotropic environments are another problem for minimal basis sets [458].

Because the core electrons of an atom are less a ected by the chemical environment than the valence electrons, the core electrons can be treated with a minimal basis set while the valence electrons are treated with a larger basis set. This is known as a split-valence basis set. In these bases, the AOs are split into two parts: an inner, compact orbital and an outer, more di use one. The coe cients of these two kinds of orbitals can be varied independently during construction of the MOs. Thus, the size of the AO can be varied between the limits set by the inner and outer functions. Basis sets that similarly split the core orbitals are called double zeta, DZ (implying two di erent exponents) or triple zeta, TZ (implying three di erent exponents). For example, the 3-21G notation of split valence basis set means that the core orbitals are represented by three Gaussians, whereas the inner and outer valence orbitals consist of two and one Gaussians, respectively. If we were to name bases consistently, of course, this one would be labeled STO-3-21G, but the STO is customarily omitted from all split-valence descriptors. Two other split-valence bases are the 6-31G and the 6-311G. Both have six Gaussian cores. The 6-311G is a triply split basis, with an inner orbital represented by three Gaussians, and middle and outer orbitals represented as single Gaussians. The triple split improves the description of the outer valence region.

Further improvement of the basis set is achieved including polarization functions in the basis set. For example, this is done by adding d-orbitals to the basis of all atoms having no d-electrons. For typical organic compounds these are not used in bond formation, as are the d-orbitals of transition metals. They are used to allow a shift of the center of an orbital away from the position of the nucleus. For example, a p-orbital on carbon can be polarized away from the nucleus by mixing into it a d-orbital of lower symmetry. One obvious place where this can improve results is in the modeling of small rings; compounds of second-row elements also are more accurately described by the inclusion of polarization. The presence of polarization functions is indicated in the Pople notation by appending an asterisk to the set designator. Thus, 3-21G* implies the previously described split valence basis with polarization added. Typically, six d-functions (x2, y2, z2, xy, xz, and yz), equivalent to five d-orbitals and one s, are used (for computational convenience). Most programs can also use five real d-orbitals. An alternative description of this kind of basis is DZP: double zeta, polarization. A second asterisk, as in the 6-31G** basis set, implies the addition of a set of p-orbitals to each hydrogen to provide for their polarization. Again, an alternative notation exists: DZ2P(double zeta 2 polarization). An asterisk in parentheses signals that polarization functions are added only to second-row elements. Another alternative to the asterisk for specifying polarization functions is (d), placed after the G.

8.1 Basis Sets in the Electron-structure Calculations of Crystals

289

To provide more accurate descriptions of anions, or neutral molecules with unshared pairs, basis sets may be augmented with so-called di use functions. These are intended to improve the basis set at large distances from the nuclei, thus better describing the barely bound electrons of anions. Processes that involve changes in the number of unshared pairs, such as protonation, are better modeled if di use functions are included.

The augmentation takes the form of a single set of very di use (exponents from 0.1 to 0.01) s and p orbitals. The presence of di use functions is symbolized by the addition of a plus sign, +, to the basis set designator: 6-31+G. (Since these are s- and p-orbitals, the symbol goes before the G.)

Again, a second + implies di use functions added to hydrogens; however, little improvement in results is noted for this addition unless the system under investigation includes hydride ions.

All of the codes for molecular ab-initio calculations o er at least one set of di use functions. Still more extensive basis sets exist, and are described by more complicated notation.

Let us summarize the notations used for molecular GTO basis sets. Basis sets denoted by the general nomenclature N-M1G or N-M11G, where N and M are integers, are called Pople basis sets. The first, N-MlG, is a split-valence double-zeta basis set while the second, N-M11G is a split-valence triple-zeta basis set. The integers N and M in the basis set name give the number of Gaussian primitives used. For example, in the split-valence double-zeta basis set 6-31G for a carbon atom, the first number (N=6) represents the number of Gaussian primitives used to construct the core orbital basis function (the 1s function). The second two numbers (M=3 and 1) represent the valence orbitals, 2s, 2s , 2p(3) and 2p (3). The first number after the dash in the basis set name (3 in this case) indicates the number of Gaussian primitives used to construct the 2s and 2p(3) basis functions. The second number after the dash (1 in this case) gives the number of Gaussian primitives used to construct the 2s and 2p (3) basis functions. There are two common methods for designating that polarization functions are included in a basis set. The first method is to use * or ** after the Pople basis set name; for example, 6-31G* or 6-31G**. The single * means that one set of d-type polarization functions is added to each nonhydrogen atom in the molecule. The double ** means that one set of d-type polarization functions is added to nonhydrogens and one set of p-type polarization functions is added to hydrogens. The second method for including polarization functions in the basis-set designation is more general. It is indicated by the notation (ll,l2) following the Pople basis-set name; for example, 6-31G(d) or 6-31G(d, p). The first label indicates the polarization functions added to nonhydrogen atoms in the molecule. The notations 6-31G(d) and 631G(d, p) mean that one set of d-type polarization functions is added to all nonhydrogens. The notation 6-31 l(2df ) means that two sets of d-type and one set of f -type polarization functions are added to nonhydrogens. The second label in the notation (ll,l2) indicates the polarization functions added to hydrogen atoms. The basis set 6-31G(d) has no polarization functions added to hydrogen, while the basis 6-31G(d, p) has one set of p-type polarization functions added to hydrogen atoms. The basis set 6-31 1G(2df , 2pd) has two sets of p-type and one set of d-type polarization functions added to hydrogen atoms. The use of di use functions in a Pople basis set is indicated by the notation + or ++. The + notation, as in 6-3l+G(d), means that one set of sp-type

290 8 Basis Sets and Pseudopotentials in Periodic LCAO Calculations

di use basis functions is added to nonhydrogen atoms (4 di use basis functions per atom). The ++ notation, as in 6-31++G(d), means that one set of sp-type di use functions is added to each nonhydrogen atom and one s-type di use function is added to hydrogen atoms.

In Table 8.2 we give a list of basis sets of orbitals that are commonly used in modern MO calculations. The H and C atomic orbitals that are included are listed. The first set contains “Gaussian-like orbitals”. Outside of the STO-3G basis set, most Gaussian basis sets are “split-valence”, which means that they use di erent numbers of Gaussian functions to describe core and valence atomic orbitals. Thus, a 6-31G basis set uses 6 Gaussians for the core orbitals, and two sets of Gassians for the valence orbitals, one with 3 Gaussians and another with one. Adding more Gaussians allows more flexibility in the basis set so as to give a better approximation of the true orbitals. Therefore, although some of the basis sets incorporate the same AOs, the larger ones provide a much better description of them. For each basis set, polarization (*), and di use functions (+) can also be added, which add flexibility into the basis set.

Table 8.2. The basis sets and orbitals they include

Basis	AOs on C*	AOs on H
STO-3G	1s, 2s, 2px, 2py 2pz	1s
3-21G*	1s, 2s, 2p, 3s, 3p	1s, 2s
3-21+G*	1s, 2s, 2p, 3s, 3p, 4s, 4p	1s, 2s
6-31G	1s, 2s, 2p, 3s, 3p	1s, 2s
6-31G*	1s, 2s, 2p, 3s, 3p, 3d	1s, 2s
6-31G**	1s, 2s, 2p, 3s, 3p, 3d	1s, 2s, 2p
6-31+G*	1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p	1s, 2s
6-311G*	1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p	1s, 2s, 3s
6-11++G(2df, 2pd)	1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f	1s, 2s, 2p, 3s, 3p, 3d, 4s

Alternate basis sets that are commonly used are the Dunning correlation-consistent polarized valence X zeta basis sets, denoted cc-pVXZ, see Table 8.3. Dunning pointed out that basis sets optimized at the Hartree–Fock level might not be ideal for correlated computations [462]. The “correlation consistent” basis sets are optimized using correlated wavefunctions and cc-pVXZ means a Dunning correlation-consistent, polarized valence, X-zeta basis; X=D,T,Q,5,6,7. In particular, the cc-pVDZ for C atom

Table 8.3. Correlation-consistent polarized valence X zeta (XZ) basis sets

Basis	AOs on C	AOs on H
cc-pVDZ	1s, 2s, 2p, 3s, 3p, 3d	1s, 2s, 2p
cc-pVTZ	1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f	1s, 2s, 2p, 3s, 3p, 3d
cc-pVQZ	1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f, 5s, 5p,	1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p,
	5d, 5f, 5g	4d, 4f
cc-pV6Z	total of 7s, 6p, 5d, 4f, 3g, 2h, i