Quantum Chemistry of Solids / 23-Modeling and LCAO Calculations of Point Defects in Crystals

10

Modeling and LCAO Calculations of Point Defects

in Crystals

10.1 Symmetry and Models of Defective Crystals

10.1.1 Point Defects in Solids and Their Models

The theory of perfect crystalline solids explains those bulk properties of crystals that do not depend on boundary e ects and other defects of the structure. However, real solids do not demonstrate translational symmetry. Boundaries and other regions of disruption of translational symmetry called defects are always present. Many practical applications of solids are based on the use of the properties caused by defects. By varying the defect structure of solids it is possible to change their physical and chemical properties in such a way that the defective crystals find useful applications. As an example, we mention TiO2 crystal that has been successfully applied as a semiconductor photocatalyst with high oxidizing power and high resistance to photoand chemical corrosion. However, the relatively large bandgap ( 3 eV) does not permit e cient absorption of visible light and hence prevents TiO2 from being used in largescale environmental applications. Chemical doping of TiO2 allows the bandgap to be reduced. The theoretical study of the doped TiO2 helps to solve the important problem: how to best manipulate the gap while maintaining the beneficial photocatalytic properties [677].

The defects in solids can be classified according to the dimensions of the region of translation symmetry disruption. When one or a few nearest host crystal sites are disturbed, we speak of point (zero-dimensional) defects, called also local defects. Also known are extended defects that introduce structural imperfections in lattice directions - linear (one-dimensional) defects or in the lattice planes (planar or two-dimensional defects). The surface of a crystal and dislocations are the important examples of two-dimensional and linear defects, respectively.

The point defects, in turn, are classified as native (intrinsic) and substitution defects. The intrinsic point defects appear as a vacancy (the absence of an atom in a crystal lattice position) or as an interstitial defect (the presence of the host crystal atom in an interstitial position). The host crystal atoms can be substituted for another atom of a di erent chemical species at a regular lattice site or at the interstitial position (impurity center or substitution defect). The point defects can also be classified as neutral and charged relative to the host crystal lattice. The perturbation of a solid by

410 10 Modeling and LCAO Calculations of Point Defects in Crystals

the charged point defect includes the short-range (local) and long-range (Coulomb) parts. The former is reproduced in the calculations of the su ciently small fragments of the defective crystal, the calculation of the latter requires special methods, taking into account the polarization of the surrounding crystal by the point defect.

In what follows we consider, as examples, LCAO calculations of di erent types of point defects in oxides: native point defects – interstitial oxygen atom in MgO crystal and neutral oxygen vacancy (F-center) in corundum Al2O3 and SrTiO3 crystals; substitution defects (vanadium-doped rutile TiO2 crystal, iron impurity in SrTiO3 crystal). The calculations of the charged point defects are demonstrated by a charged oxygen vacancy (F+ center) in corundum Al2O3 crystal.

For low defect concentration it becomes appropriate to model a single point defect in an environment of the remaining solid. In such a model the translation symmetry is completely absent so that the crystal with a single point defect can be seen as a gigantic molecule. However, in the case of a solid solution the single-defect model is not appropriate as the stoichiometry change is introduced by regular substitution of the host-crystal atoms by those of other chemical species. In this case the periodic point-defect model is more appropriate. As an example, we discuss in Sect. 10.3 the modeling of BaxSr1−xTiO3 solid solutions.

The calculational methods of quantum chemistry are widely applied to the point defects in solids. This application is made after the choice of one of the existing defective crystal models, (see Fig. 10.1).

3HUIHFW FU\VWDO SHULRGLF V\VWHP

3ULPLWLYH XQLW FHOO

&U\VWDO ZLWK VLQJOH SRLQW GHIHFW DSHULRGLF V\VWHP

0ROHFXODU FOXVWHU				0RGHOV ZLWK SHULRGLF
PRGHOV				ERXQGDU\ FRQGLWLRQV
(PEHGGHG	6DWXUDWHG		)UHH	&\FOLF	6XSHUFHOO
FOXVWHU	FOXVWHU		FOXVWHU	FOXVWHU
		++
	+	+
	+	+
		++

Fig. 10.1. Defective crystal models

If a single point defect is introduced into an otherwise perfect crystal, the translational symmetry is, in principle, lost completely (see Fig. 10.1), and equations should be solved for all atoms of the solid, i.e. for the aperiodic system [294]. Obviously, the application of some kind of simplified model is desirable. In many cases the electronic states of defects in a crystal are localized in some relatively small region. The degree of this localization depends on the nature of the defect and of the host crystal. The local

10.1 Symmetry and Models of Defective Crystals

411

nature of a single point defect allows a smaller piece of a crystal to be taken (called a cluster) but its size must be chosen in such a way that there is at least one shell of atoms between the defect zone and the cluster surface that remains undisturbed. The obvious way is to separate the part of the crystal perturbed by the defect from the still crystalline background, and treat only the former in an explicit manner. On the one hand, the need for economizing calls for a model consisting of as few atoms as possible. On the other, the explicitly treated part of the crystal should, in principle, extend far enough for the e ect of the defect to become negligible [294]. This means, up to the point where the amplitude of the localized wavefunctions, the deviations of charge density and of host-atom positions relative to the unperturbed case become close to zero. In practice, this is assumed to be for a group of atoms around the defect (cluster). The three criteria above are almost never satisfied to a necessary degree with clusters that can be sequeezed into the computer. Therefore, at least some kind of convergence test in all three respects is proper.

The electronic structure of the molecular cluster can be calculated using any of the methods developed for the molecules. However, the problem arises at the molecular cluster surface, i.e. with the representation of the rest of the crystal. As is shown schematically in Fig. 10.1, there are di erent possibilities for this representation. In molecular-cluster models the group of atoms chosen is embedded into the crystalline environment (embedded-cluster model) or the cluster surface atoms are saturated by hydrogen or other species atoms (saturated-cluster model). In the most crude model the free cluster (neutral or charged) is chosen.

The models with periodic boundary conditions (the supercell and the cyclic-cluster models) allow calculation of the one-electron states of perfect and defective crystals at the same level of approximation. The supercell model (SCM) and cyclic-cluster model (CCM) have both similarities and discrepancies. One similarity is that in both models not a standard primitive unit cell but an extended unit cell (supercell or large unit cell) is considered. The discrepancy is that the periodic boundary conditions in the SCM are introduced for the infinite crystal or its main region, but in the CCM model – for the extended unit cell itself.

The calculation schemes usually used for point defect include: 1. the choice of the model of the defective crystal; 2. the choice of the Hamiltonian (Hartree–Fock, DFT or hybrid, semiempirical); 3. the choice of the basis for the one-electron Bloch functions decomposition – linear combination of atomic orbitals (LCAO) or plane waves (PW).

SCM is used as a rule for the neutral-point-defects calculations (for the charged point defects the field of periodically repeated charge has to be suppressed in one or another way). The molecularand cyclic-cluster models are more universal as they can be applied both for the neutral and charged point defects.

In the SCM the calculations with HF or hybrid Hamiltonians are made in the LCAO approximation, DFT Hamiltonians are used both in the LCAO and PW representations. CCM can be practically realized with the semiempirical LCAO Hamiltonians.

In SCM we let the defects be situated periodically and try to make the separation between defects as large as possible. If the extended unit cell is large enough the defects are separated by large distances and do not a ect each other’s electron structure so that the results of the application of SCM and CCM models become close. The bandwidth of defect states depends primarily on the degree of overlap of the functions

412 10 Modeling and LCAO Calculations of Point Defects in Crystals

describing the defect electron states from di erent supercells and decreases rapidly with increasing defect period. Therefore, this bandwidth can be used as the criterion of the convergence of the SCM results to those of CCM. The cyclic-cluster model is conceptually a supercell-type approach but is technically more closely related to the simple molecular-cluster model. SCM introduces the artificial point-defect periodicity, CCM describes the single point defect.

All the approaches to the theoretical description of defective crystals use information about the symmetry of the system or its model. As mentioned above, a single defect embedded in a crystal disrupts the translational symmetry of a perfect crystal so that it may be considered as a gigantic molecule with a point-symmetry group inherent to molecules. There are two cases: an atomic type point defect, which occupies one point of a crystal lattice or an interstitial position and can be a substitutional impurity, vacancy or interstitial atom; and a molecular type point defect, which occupies several atomic or interstitial points of a crystal lattice and can be composed of an impurity molecule or a cluster of several vacancies at neighboring lattice points. In the first case the symmetry group of the defect crystal is fully determined by the site symmetry of the point q where the atomic defect appears. In a crystal with a symmorphic space group the atomic defect may occupy the position q with the symmetry of the crystal class or one of its subgroups. In nonsymmorphic crystals the point group of the crystal with a single point defect of atomic type is always a subgroup of the crystal class. In a crystal with point defects of molecular type the center of the impurity molecule is situated at a point with some site symmetry. A molecular defect has its own point symmetry so that the point symmetry of the whole system is determined by the common elements of two groups: the point group of the isolated molecule and the site-symmetry group of the site where the impurity molecule is situated. However, it is necessary to also take into account the orientation of the impurity molecule with respect to the crystal symmetry axes.

It can be assumed that when a point defect appears the configuration of the crystal matrix around the defect does not change (the model of a rigid lattice). In reality, this assumption is approximately correct only for some point defects and as a rule only for the ground electron state. Excitation of the defect electrons causes significant reconstruction of the defect’s surroundings so that the point symmetry of the entire system may change. In many calculations, the distortion of the crystal lattice by a defect is at first neglected. Then, this distortion is taken into account with approximate wavefunctions obtained for the rigid-lattice model. Therefore, initially, the symmetry is approximated in the framework of the rigid-lattice model. The knowledge of the actual symmetry of a crystal with a point defect is necessary for correct understanding of all its properties: the symmetry determines the selection rules for optical transitions in the defect, the symmetry and the splitting of local energy levels in external fields, the features of EPR and NMR spectra, etc.

To understand the nature of a point defect in a crystal and the degree of its influence on the properties of the crystal matrix it is necessary to relate the local energy levels of the defect to the energy-band structure of the perfect crystal. But these two systems (crystal with defect and perfect crystal) have di erent symmetries and the classification of electron states is made according to irreps of either a point group (for a crystal with a single defect) or a space group (for a perfect crystal).

10.1 Symmetry and Models of Defective Crystals

413

In the molecular-cluster model it is rather easy to establish the relationship between energy levels and one-electron states of a molecular cluster with and without a point defect. The symmetries of both systems are described either by the same point group or by a point group that is a subgroup of the other (in the case of a moleculartype defect). Hence, in the cluster model the relationship between the classification schemes of electron energy levels and states of perfect and imperfect crystals is simple. But the relationship between the cluster electron energy structure and that of a perfect crystal is much more complicated. In the models using PBC the application of the site-symmetry approach is quite useful [13]. The single-defect localized electron states of a given energy level span the space of an irrep of defect point-symmetry group FD. The band states of a perfect crystal are classified according to irreps of the space group G. It is useful to determine which band and localized states are allowed by symmetry to mix (e.g. , for calculating the electron structure from atomic basis functions). We consider the appearance of a point defect as a perturbation of a perfect crystal. According to perturbation theory, only states with the same symmetry may interact with one another. The common symmetry group of both systems is FD G. Let β be an irrep of FD that describes one of the defect states. To establish the possibility of its mixing with the perfect crystal states of symmetry D( kγ) it is su cient to know whether the restriction D( kγ) ↓ FD contains the irrep β. If the state of symmetry D( k0γ) does not contain the state of symmetry β, then the contribution of the states with k near k0 is small according to the perturbation theory, although it is not equal to zero due to the symmetry. As an example, let us consider the s-states of an impurity at a cation site (Wycko position a, site group D2h s-state has symmetry ag) or at an anion site (Wycko position f , site group C2v , s-state has symmetry a1) in rutile TiO2. From band calculations we know the symmetry of states on the boundaries of the forbidden gap in a rutile TiO2 crystal (see Chap. 9): Γ1+(the bottom of the lowest conduction band) and Γ3+ (the top of the highest valence band). From the table of induced representations of the space group D414h we find Γ1+ ↓ D2(ah) = ag ; Γ3+ ↓ D2(ah) = b1g , i.e. the s-states of an impurity may mix with the states of the bottom of the lowest conduction band, but not with the states of the top of the uppermost valence band. The anion site is at the Wycko position f

(Ff = C2v ). We get Γ1+ ↓ C2(fv) = a1; Γ3+ ↓ C2(fv) = b2, i.e. the s-states of an impurity at an anion site may mix with the states of the bottom of the lowest conduction

band but not with the states of the top of the uppermost valence band. From this consideration it follows that the defect local levels due to the s-states of the impurity both at Ti and O sites split from the conduction-band bottom. Such information is useful for the study of doping influence on the rutile crystal bulk properties.

In the next sections we consider in more detail the defective-crystal models mentioned above.

10.1.2 Symmetry of Supercell Model of Defective Crystals

The recent trends in the theory of the point defects in solids and of the crystalline surfaces, formally aperiodic systems, are connected with the widespread application of periodic boundary conditions (PBC) and computer codes developed for the perfect crystals, see [568, 678, 679] and references therein. This allows one to use the same numerical schemes both for the host and defective crystal to study changes induced

414 10 Modeling and LCAO Calculations of Point Defects in Crystals

by a point defect or surface: additional local energy levels in the optical gap, lattice relaxation around defects, etc . As was noted above, in the theory of point defects two models with PBC are used: the supercell model (SCM) and the cyclic-cluster model (CCM).

The application of the supercell model to the defective crystals requires consideration of periodic systems with a su ciently large number of atoms in the unit cell. The possibilities of the supercell model extend if the full symmetry of the object is taken into consideration. It was demonstrated [681–683] that the study of the symmetry of a crystal with a periodic defect permits, in some cases, investigation of the dependence of the results of electronic-structure calculations on the period of a defect by only changing the symmetry of the system without any augmentation of the supercell. The symmetry of the crystal with a periodic defect is determined by the site symmetry of the defect in the crystal and by the symmetry of the host-crystal matrix. Let a point defect (impurity atom or molecule, one or a few vacancies) occupy a position q in a perfect crystal with a space group G (crystal class F). A site-symmetry group of the defect in the crystal SD consists of common elements of two groups: of the symmetry group S(0)D of the defect itself and the site-symmetry group Sq of the position q in the crystal occupied by the defect. The group SD depends on the mutual orientation of the symmetry elements of the groups S(0)D and Sq.

Let us consider now a periodic structure that arises in the supercell model when the embedded defect is periodically repeated and occupies in this structure some position Q with site-symmetry group SQ = SD. The symmetry of the obtained periodic structure is characterized by some space group GD. One seeks for all the possible space groups GD = TAFD of the defective crystal for a given host crystal (space group G) and for a given point defect in the crystal (point group SD). Here, translation group TA includes translations A of the supercell. Some symmetry operations disappear when one goes from the space group G to the space group GD. Therefore, the group GD has to be a subgroup of GD G with a crystal class satisfying the condition SD FD F. The possible space groups GD of the crystal class FD are those that have the group SD as a site-symmetry subgroup. In this way, one obtains the list of space groups GD that may describe the symmetry of the supercell model of a defective crystal for a given site symmetry SD of the embedded defect and space group G of a host crystal.

In the framework of the same space group GD the periodical structures may di er by the length of supercell basic translation vectors A1, A2, A3 for the same type of Bravais lattice. These vectors have a definite orientation with respect to the symmetry elements of the group GD, and sometimes there is a definite relation between their lengths. In addition, they have to be integer linear combinations, see (4.77), of basic translation vectors of the host perfect crystal. This combination defines the transformation matrix l with the determinant L (the number of primitive unit cells in the supercell). As was noted, this transformation is called a symmetric one if the point symmetry of the Bravais lattice of supercells is the same as that of the host-crystal Bravais lattice, see Chap. 4. Use of the symmetric transformation for the supercell generation allows the point symmetry of the defective crystal in the supercell model to be maintained as high as possible. These conditions determine the matrix l, i.e. the translational subgroup TA of the symmetry group GD. Finally, it is necessary to verify whether the obtained group GD is a subgroup of the symmetry group of the

10.1 Symmetry and Models of Defective Crystals

415

host crystal. This condition assures that all the atoms of the system transform into themselves under the operations of the group GD. If GD G, then GD = GD; if

)

G	the list of the possible groups
GD. G, then the group GD has to be excluded from	)	)

D

Finally, the generation of the possible space groups with a periodical defect in the supercell model consists of the following steps [683]:

(i) determination of the site group SD of the defect in the crystal; (ii) determination of the crystal classes satisfying the condition SD FD F; (iii) determination in the space groups of these classes those that have the site-symmetry subgroups SD; (iv) generation of the matrix l and the supercell translation vectors Ai by symmetric transformation of the host crystal basic translations; (v) verification of the condition GD G.

The groups GD of a supercell model with one point defect for a supercell are symmorphic, they belong to the crystal class FD = SD with all the types of crystal lattices possible for this crystal class. The point symmetry of the cyclic-cluster coincides for the host crystal – with the point-symmetry group F, for the defective crystal – with the point-symmetry group SD.

Let us consider some examples. In MgO crystal the supercells, containing 8, 16 and 32 atoms (S8, S16, S32), are obtained by a linear symmetric transformation of

the fcc lattice basic translation vectors with matrices
	1	1	−1				2 0 0			3 −1 −1
l(4) =	1	−1	1		,	l(8) =	0 2 0	, l(16)	=	−1 3 −1
	−1	1	1				0 0 2			−1 −1 3

Superscript (n) in l(n) denotes the number of primitive unit cells in the supercell. The supercell translation vectors for A1, A2, and A3 for l(4), l(8), l(16) correspond to simple cubic, face-centered-cubic, and body-centered-cubic lattices, respectively. The host crystals, consisting of the corresponding supercells, have the symmetry of cubic space groups Oh1 , Oh5 , and Oh9 , respectively. For the isoelectronic Be, Ca impurities in the Mg site the site-symmetry group coincides with the point-symmetry group of the host crystal, i.e. the space groups of the defective crystals are the same as for the host crystal. The Li impurity atom is displaced from the Mg site along the fourth order symmetry axis (the Li atom site symmetry is C4v ). As a result, the space groups of the defective crystal are now tetragonal – C4(1)v , C4(9)v , and C4(9)v , respectively (the face-centered lattice is absent in the tetragonal system).

An additional neutral interstitial oxygen Oi atom as a point defect in MgO crystal can have several configurations. In three of these (called v, f , and e) the oxygen atom is at the volume, face, or edge centers, respectively, of the cubic unit cell. Fig. 10.2 shows volume-(a), face-(b) centered configurations and a (110)-oriented dumbbell (see below) configuration (c). The point symmetry of the v, f and e configurations is Td, D2h, and C4v , respectively. The space groups for MgO with these centers in the supercell model depend on the supercell chosen and they are given in Table 10.1. The other three configurations vd, f d, and ed are so-called dumbbell-shaped defects formed when the Oi is moved towards a nearest-neighbor O2− lattice anion along <111>, <110>, or <001> directions, respectively, the lattice anion being simultaneously displaced from its site along the same direction. The center of the dumbbell is at the lattice site, and the point symmetry of these defects is D3d, D2h, and D4h, respectively. The space

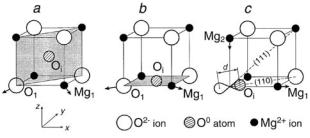
416 10 Modeling and LCAO Calculations of Point Defects in Crystals

Fig. 10.2. Configurations of the interstitial oxygen atom in MgO

groups of MgO containing these defects are given in the last three lines of Table 10.1. The results of Table 10.1 were obtained using the list of subgroups of the space groups given on the Internet site www.cryst.ehu.es. For example, the supercell transformation with the matrix l(4) changes the host-crystal space group from Oh5 to Oh1 . Choosing from the list of subgroups of space group Oh1 those symmorphic subgroups that refer to the crystal class Td (point symmetry of the v configuration), we obtain directly the result given in the third column of Table 10.1.

Table 10.1. Space-group symmetry for the supercell model of an oxygen-atom interstitial Oi in MgO crystal [682]

			Supercells
Center	FD	l(4)	l(8)	l(16)
v	Td	Td1 (215)	Td2 (216)	Td3 (217)
f	D2h	D219h(65)	D225h(71)	D225h(71)
e	C4v	C41v (99)	C49v (107)	C49v (107)
vd	D3d	D35d(166)	D35d(166)	D35d(166)
f d	D2h	D219h(65)	D225h(71)	D223h(69)
ed	D4h	D41h(123)	D417h(139)	D417h(139)

The next example – the impurity atom on the Ti site of rutile structure with the space group D414h. There are two titanium atoms in the primitive unit cell, occupying the two-site Wycko position a with coordinates (000) and ( 12 12 12 ). An impurity atom replaces a Ti atom with the site symmetry D2h. Therefore, the space group of the defective crystal belongs to the crystal class D2h. Four possible symmetric supercell transformations for the space group D414h are given in Table 6.3. The first of them maintains the simple tetragonal lattice of the host crystal, the other three transform it to the body-centered tetragonal lattice. Respectively, the possible symmetry groups of the defective crystal are the following: D21h, D219h, D223h, D225h.

10.1 Symmetry and Models of Defective Crystals

417

In the Ti atom site-symmetry group two of three second-order axes are directed along the diagonals of the square, see Chap. 2. In the standard setting of the space groups with D2h point symmetry all the three second-order axes are directed along the Cartesian coordinate axes. This di erence must be taken into account [683].

The point symmetry of the cyclic-cluster model coincides with point groups F and FD for the host and defective crystal.

10.1.3 Supercell and Cyclic-cluster Models of Neutral and Charged Point Defects

In the point-defect calculations there are two criteria to be met: the model used for solving the quantum-mechanical problem has to describe su ciently well both (i) the extended crystalline states and (ii) the localized states of a single point defect. The CCM can be defined from the two points of view: it can be regarded either as the application of the Born– von Karman cyclic boundary conditions directly to the large unit cell (supercell), or as the band-structure calculation on SCM with (A) applying the k = 0 approximation, and (B) neglecting interactions beyond the Wigner–Seitz cell corresponding to the supercell chosen. The SCM have no restrictions like A and B and thus CCM could be considered as a special approximation to the SCM.

The economic approach to a single-point-defect study in a model with PBC consists of three stages [680].

In stage 1 the band-structure calculation of a perfect crystal is performed, in order to fix the shape and size of the supercell that reasonably models the host crystal, i.e. when the above-described condition (i) is met. These calculations are made using a primitive unit cell and k-sampling in the usual (primitive) BZ.

The one-to-one correspondence was demonstrated between a fixed k-mesh and the supercell in a real space, see Equations (4.77), (4.80) and (4.84). Due to the one-to- one correspondence between k-point sampling and the supercell size in a real space it is possible to find such a k-mesh that ensures a compromise between its size and a reasonable reproduction of the totaland one-electron energies, as well as the electrondensity distribution in the host crystal. At this stage, the k-point sets satisfying (4.84) are used.

In stage 2 the calculations are made for a defective crystal using SCM, in order to check the above-described criterion (ii). It is reasonable to begin from the smallest supercell, chosen at stage 1, i.e. corresponding to the converged results of the band calculations. The supercell shape should be such as to exploit the point symmetry of the defect as far as possible. In the particular case of the cubic SrTiO3 crystal cubic supercell of 80 atoms (L = 2 × 2 × 2, the diagonal matrix l in transformation (4.77) is taken) may be used for a perfect crystal in the HF calculations but larger supercells are necessary in the DFT-PWGGA calculations [680]. When estimating the defect– defect interaction from the calculated defect bandwidth in the second stage, one makes a decision about the need for a further increase of the supercell. In particular, the Fe impurity at the Ti site bandwidth in the HF calculations still changes when the supercell is increased from 80 to 160 atoms [680]. This means that the local states induced by the point defect are su ciently well localized only in the larger, 160-atom supercell [680]. That is, in stage 2 the comparison of supercell results for di erent k-meshes allows us to decide if it is necessary to further increase a supercell, in order

418 10 Modeling and LCAO Calculations of Point Defects in Crystals

to surpass artificial defect–defect interaction. When energies at k = 0 and nonzero k supercell calculations turn out to be close, this means that the corresponding cyclic cluster is appropriate for the single-point-defect study as CCM corresponds to the Γ point only consideration for the supercell chosen.

In the most time-consuming stage 3 the CCM is used (i.e. the band-structure calculations for the chosen supercell are performed only at k = 0) for the determination of the equilibrium geometry, i.e. relaxation of the crystalline lattice around the point defect and calculation of other defective crystal properties.

As is seen, the approach described combines both supercell and cyclic-cluster models of the defective crystal and di ers from the traditional supercell calculations by an attempt to exclude in stage 3 the spurious point-defect periodicity. This exclusion allows us formally to escape periodic repeating of the crystalline lattice relaxation around the point defect. Furthermore, the di erent charge states of the point defect could be also considered in stage 3 without principal di culties since in CCM the charge is not periodically repeated over the lattice.

The defect-formation energy is an important property of the defective crystal. The formation energy ∆Ef of a neutral defect in CCM is given by

∆Ef = Ed − EB + ER − EA

(10.1)

where EB is the bulk-crystal total energy, Ed is the total energy of the cyclic cluster with the point defect, EA and ER the energies of the added and removed species, respectively. The bulk crystal energy EB = LE(0), where L is the number of primitive cells in the cyclic cluster and E(0) is the energy per primitive cell. As an example, for ionic MgO crystal the formation energy of X substitution impurities (X=Ca, Be substitutes Mg atom), [684], can be given in terms of the isolated atoms or isolated ions

∆EXL = EMgO−X − LEMgO(0) + EMg2+ − EX2+	(10.2)
∆EXL = EMgO−X − LEMgO(0) + EMg − EX	(10.3)

When the relaxation is taken into account (shifting of some nuclei around a defect from a reference bulk-crystal situation) the total energy Ed is corrected by the relaxation energy Erel.

The oxygen-removal energy for MgO crystal ∆Ef (formation energy of neutral oxygen vacancy, also called an F center) is defined as the energy of the system, containing the F center, plus the energy of an isolated oxygen atom minus the energy of the perfect crystal [685]. In the LCAO approximation the energies of added or removed atoms are calculated in the same numerical scheme that is used for the bulk and defective crystal calculation (the atomic basis is used that is appropriate for a free atom, see Chap. 9). In PW calculations the energy of the isolated atom is obtained by calculations on a number of periodic systems, containing one atom per increasing supercells, and the final size of the supercell is taken large enough to ensure that the interaction between atoms introduces a su ciently small error (this error was 0.01 eV in calculations [685]). Within the supercell approach, ∆Ef should tend to a welldefined limit with increasing supercell size. For a defect to be considered as single, su ciently large supercells must be adopted to avoid spurious interactions among neighboring defects.