Хурсан - Лекции по квантовой механике и квантовой химии / 06Lecture-05

Лекция 5.

Решение уравнения Шредингера для атома водорода (и водородоподобных атомов).

5.1. Уравнение Шредингера для атома водорода.

Все члены уравнения Шредингера для атома водорода (и водородоподобных атомов, имеющих заряд ядра Z и единственный электрон) мы уже упоминали. Оператор потенциальной энергии в соответствии с законом Кулона равен

ˆ

Ze2

V

(r) = −

.

r

Гамильтониан в этом случае примет вид

ˆ

ˆ

ˆ

h2

2

Ze2

H = T

+V

= −

−

,

2m

r

e

а стационарное уравнение Шредингера запишется в виде

h

2

2

Ze

2

−

−

Ψ(x, y, z)

= EΨ(x, y, z).

2m

r

e

5.2. Разделение переменных.

Удобным способом решения уравнения Шредингера является замена декартовых координат на полярные: вместо x, y, z вводятся расстояние r и два угла – θ и ϕ.

Связь между сферическими и декартовыми координатами показана на рисунке, формулы пересчета из одной системы координат в другую имеют вид:

x = rsinθcosϕ;	0	≤ r < ∞;	r = (x2 + y2 + z2)1/2;
y = rsinθsinϕ;	0	≤ θ ≤ π;	θ = arccos(z/r);
z = rcosθ;	0	≤ ϕ ≤ 2π;	ϕ = arctg(y/x);
	dv = dx dy dz = r2sinθ dr dθ dϕ.

В сферических координатах оператор Лапласа принимает вид:

2

1

∂

2

∂

1

∂

∂

1

∂2

=

r

+

sinθ

+

.

r 2

r 2 sin 2

θ ∂ϕ2

∂r

∂r

r 2 sinθ ∂θ

∂θ

Тогда уравнение Шредингера примет вид:

2

1 ∂

2

∂Ψ

1

∂

∂Ψ

1

∂2Ψ

r

+

sinθ

+

+

r 2 sin2

θ ∂ϕ2

r 2 ∂r

∂r

r 2 sinθ ∂θ

∂θ

				Ze	2
	2me
+			E +			Ψ = 0.
	h	2		r

Z

A

θr

O 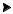Y

ϕ

X

Чтобы разделить переменные представим волновую функцию в виде

произведения радиальной и угловых частей:

Ψ(r,θ,ϕ) = R(r) Θ(θ) Φ(ϕ),

ΘΦ ∂

2

∂R

RΦ ∂

∂Θ

RΘ ∂2Φ

r

+

sinθ

+

+

r

r 2 sin2

θ ∂ϕ2

r 2 ∂r

∂r

2 sinθ ∂θ

∂θ

Ze

2

2me

+

E +

RΘΦ = 0.

h

2

r

Умножим уравнение на r2/RΘΦ и получим:

1 ∂

2

∂R

2mer

2

r

+

E +

h

2

R ∂r

∂r

1

∂

∂Θ

= −

sinθ

∂θ

−

Θsinθ ∂θ

Ze2

r=

1∂2Φ.

Φsin2 θ ∂ϕ2

Левая часть уравнения зависит только от переменной r, а правая – от угловых переменных θ и ϕ. Следовательно, обе части равны некоторому постоянному числу C, что позволяет отделить радиальную часть уравнения Шредингера:

3

d

2

dR

2me r

2

Ze

2

r

+

E +

R −CR = 0

h

2

r

dr

dr

Переменные θ и ϕ разделяются путем умножения правой части уравнения на sin2θ.

1 ∂				∂Θ		1		∂2Φ	= −C,
			sinθ		+
						Φsin 2	θ ∂ϕ2
Θsinθ ∂θ				∂θ

sinθ		∂		∂Θ	2		1 ∂2Φ
			sinθ		+C sin	θ = −			.
							Φ ∂ϕ2
Θ ∂θ				∂θ

Аналогично, левая и правая части уравнения, не зависящие друг от друга, равны константе, которую мы «мудро» обозначим как m2. При этом получаются еще два уравнения, которые мы запишем в удобной для нас форме:

d 2Φ

+ m2 = 0,

dϕ2

1 d

dΘ

m2

sinθ

2

dθ

+ C −

sin

Θ = 0.

sinθ dθ

θ

5.3. Решение Φ-уравнения.

Легко проверить подстановкой, что решением Φ-уравнения будет функ-

ция

Φ = A exp(±imϕ).

Так как при тождественных значениях угла ϕ (0 и 2π) функция должна иметь одно и то же значение, то

A exp(±im0) = A exp(±im2π) = A

и

exp(±im2π) = 1.

Используя формулу Эйлера для комплексных чисел:

cos(2πm) ± i sin(2πm) = 1,

получим m = 0, ±1, ±2, ….

Таким образом, m может принимать только целочисленные значения. Константа A находится из условия нормировки функции Φ:

2π

2π

∫Φ Φdϕ = A2 ∫eimϕe−imϕdϕ = A2 2π =1.

0

0

Окончательно имеем:

Φ= 21π exp(±imϕ).

5.4.Решение Θ-уравнения. Полиномы Лежандра.

Θ-Уравнение хорошо известно в теории дифференциальных уравнений. Оно имеет конечное решение только в случае выполнения условий

4

C = l(l + 1), l = 0, 1, 2, …, -l ≤ m ≤ l,

при этом решениями являются так называемые функции или полиномы Лежандра. Нормированные Θ-функции имеют вид

Θlm (θ) = 2l +1 (l−| m |)! 1/ 2 Pl|m| (cosθ).

2 (l+| m |)!

Функции Pl|m|(cosθ) называют присоединенными полиномами Лежандра и определяют следующим образом:

P|m| (cosθ) =

1

[1−(cosθ)2 ]|m|/ 2

d l +|m|

[(cosθ)2 −1]l .

l

2l l!

(d cosθ)l +|m|

Например, при l = 2, m = ±1

Θ2,±1

5 1 1/ 2

1

sinθ

d 3

3 [(cosθ)

2

−1]

2

=

=

2

2

2

(d cosθ)

2 3!

=	1	5 sinθ		d 2	{4[(cosθ)2 −1]cosθ}=			1	5 sinθ ×
	16	3		(d cosθ)2				4	3
×		d	[3(cosθ)2 −1] =			1	15 sinθ cosθ.
	(d cosθ)					2

Произведение функций Θ(θ) и Φ(ϕ) представляет собой угловую часть волновой функции

Ylm(θ, ϕ) = Θlm(θ) Φm(ϕ)

Функции Ylm называются шаровыми функциями или сферическими гармониками. Объединяя выражения для Θ(θ) и Φ(ϕ), запишем угловую часть в общем виде:

Y	(θ,ϕ) =		1		2l +1 (l−| m |)! 1/ 2				P|m| (cosθ) exp(imϕ).
lm			2π						l
					2 (l+| m |)!

5.5. Решение R-уравнения. Полиномы Лягерра.

Перепишем R-уравнение, введя величину боровского радиуса a0 = ħ2/(mee2) и подставив вместо постоянной C произведение l(l + 1):

d

2

R

2 dR

2E

2Z

l(l +1)

+

+

+

−

R = 0.

dr 2

a0r

r dr

a0e2

r

Это уравнение также хорошо исследовано в теории дифференциальных уравнений и в математической физике. Решение этого уравнения требует введения еще одного параметра n, принимающего только целочисленные значения, причем

n = 1, 2, 3, …; n ≥ l + 1, где l = 0, 1, 2, …, n – 1.

5

С учетом нормировки решение R-уравнения, называемой радиальной частью волновой функции, записывается следующим образом:

(n −l −1)!

1/ 2

2Z

l+3/ 2

l

Zr

2l+1

Rnl (r) = −

r

exp

−

Ln+l

(q),

3

na0

2n[(n +l)!]

na0

где q = 2Zr/na0.

Функция L2nl++l1 (q) представляет собой так называемый присоединенный полином Лягерра, который связан с полиномом Лягерра Ln+l (q) дифференциальным соотношением Родрига:

		Lu (q) =		d u		L (q),
		t	dqu			t
	где			d t
	L (q) = exp(q)					[qt exp(−q)].
	t			dqt

Приведем некоторые простые соотношения для присоединенных полиномов Лягерра:

L0	(q) = L (q); Lt−1		(q) =[(−1)t q −t] t!; Lt	= (−1)t t!,
t	t	t	t

т.е. последний полином есть число (не зависит от q). Полиномы Лягерра с различными n и l ортогональны между собой, что определяет ортогональность радиальных функций.

Определим в качестве примера радиальную часть для случая n = 3, l = 2. Выражение для R(r) в этом случае примет вид:

(3 −2 −

1/ 2

2Z

7 / 2

2

Zr

5

R3,2

(r) = −

1)!

r

−

(q) =

6[(5)!]

3

3a0

exp

3a0

L5

1 1 1

Z

7 / 2

2

Zr

5

= −

r

−

30 81 30

exp

L5 (q).

a0

3a0

Присоединенный полином Лягерра равен:

L55 = (−1)5 5!= −120.

Отсюда окончательно имеем:

		4		Z	7 / 2		2			Zr
R3,2	(r) =					r			−
		81 30						exp			.
			a0							3a0

Таким образом, уравнения Шредингера для атома водорода (и для водородоподобного атома с Z = 2, 3, и т.д.) решено. Сращивая радиальную и угловую части волновой функции, получаем:

Ψnlm = Rnl (r)Θlm (θ)Φm (ϕ) = Rnl (r)Ylm (θ,ϕ).

Например, для рассмотренных выше случаев n =3, l = 2, m = ±1:

6

4

Z

7 / 2

2

Zr

1

Ψ3,2,±1

(r,θ,ϕ) =

r

−

15 sinθ cosθ

×

81 30

exp

2

a0

3a0

1

1

Z

7 / 2

−

Zr

2

3a0

±iϕ

×

exp(±iϕ) =

r e

sinθ cosθ e .

2π

81

π

a0