08.04.09.Печать_edit

n | ind a ind a nQ , где nQ ps 1( p 1) Q		ps 1( p 1)		, т. е. имеем коли-
		n
чество различных целых чисел Q, равное	ps 1( p 1)		, и им соответствуют
		n

разные значения gnQ mod ps , причем все из последних являются вычетами степени n. Действительно, gnQ gQ n mod ps .

Задача 3.7.

Доказать, что если a – вычет степени n | ps 1(p 1), где p – нечетное

	s	ps 1	( p 1)
			n	s
	простое число, по модулю p , то a			1mod p .

Решение: По условию задачи существует некоторое значение x, такое что выполняется сравнение xn a mod ps , которое можно представить в виде gn ind x gind a mod ps , g – некоторый первообразный корень, откуда следует n ind x ind a mod ( ps ) , где (ps) = ps 1(p 1). Поскольку по условию мо-

дуль делится на n, то из последнего сравнения следует, что

n | ind a .

По-

скольку

индекс

вычета

n-й

степени

делится

на

n,

то

ind a

mod ps x ps 1( p 1) g

ind a

ps 1( p 1) gind a

ps 1( p 1)

ps 1( p 1)

x g n

n

n a

n

mod ps .

ps 1( p 1)

ps 1( p 1)

Согласно теореме Эйлера, имеем x

1mod p

s

a

n

1mod p

s

.

Задача 3.8.

ps 1( p 1)

s 1

n

s

Пусть a

1mod p , где n | p

(p 1), где p – нечетное простое

число. Доказать, что a – вычет степени n по модулю ps.

Решение: Поскольку по модулю ps имеются первообразные корни, то

				ps 1( p 1)		ind a		ps 1( p 1)
условие задачи можно представить в виде			g	n			g		mod p	s	,
где g –		некоторый первообразный корень.			Следовательно,				имеем
	ps 1( p 1)	ind a ps 1( p 1) mod ps 1( p 1)	n | ind a .				Тогда		имеем
	n

81

mod 2 ps ,

gind a

gn ind x

	ind a n
a gind a g			mod ps , т. е. существует решение сравнения
	n
xn a mod ps .

Задача 3.9.

Доказать, что число вычетов степени n | p(p 1), где p – нечетное про-

стое число, по модулю 2ps равно n.
Решение: Рассмотрим сравнение xn a mod 2 ps ,	где a –	квадратичный
вычет и НОД(a, (2ps)) = 1 (следовательно,	имеем	также и

НОД(x, (2ps)) = 1). Известно, что по модулю 2ps имеются первообразные корни. Пусть g – некоторый первообразный корень. Тогда можем переписать указанное сравнение в виде откуда следует

n ind x ind a mod (2 ps ) , где (2ps) = ps 1(p 1). Поскольку по условию модуль делится на n, то из последнего сравнения следует, что

n | ind a ind a nQ , где nQ ps 1( p 1) Q		ps 1( p 1)		, т. е. имеем коли-
		n
чество различных целых чисел Q, равное	ps 1( p 1)		, и им соответствуют
		n

разные значения gnQ mod 2 ps , причем все из последних являются вычетами степени n. Действительно, gnQ gQ n mod 2 ps .

Задача 3.10.

Доказать, что если a – вычет степени n | ps 1(p 1), где p – нечетное

	s	p( p 1)
		n	s
	простое число, по модулю 2p , то a		1mod 2 p .

Решение: По условию задачи существует некоторое значение x, такое что выполняется сравнение xn a mod 2 ps , которое можно представить в виде gn ind x gind a mod 2 ps , g – некоторый первообразный корень, откуда сле-

дует n ind x ind a mod (2 ps ) ,	где	(2ps) = ps 1(p 1). Поскольку	по
условию модуль делится на n, то	из	последнего сравнения следует,	что

82

n | ind a .

Поскольку

индекс

вычета n-й

степени

делится

на

n, то

ind a

mod 2 ps x ps 1( p 1)

ind a

ps 1( p 1)

gind a

ps 1

( p 1)

ps 1( p 1)

x g n

g

n

n

a

n

mod 2 ps

Согласно теореме Эйлера, имеем

ps 1

ps 1( p 1)

x

( p 1)

1mod 2 p

s

a

n

1mod 2 p

s

.

Задача 3.11.

ps 1 ( p 1)

s 1

n

s

(p 1) и p –

Пусть a

1mod 2 p ,

где n | p

нечетное простое

число. Доказать, что a – вычет степени n по модулю ps.

Решение: Поскольку по модулю 2ps имеются первообразные корни, то

ps 1( p 1)

ind a

ps 1

условию задачи представить в виде g

n

g

( p 1)

mod 2

некоторый

первообразный

корень.

Следовательно,

ps 1( p 1)

ind a ps 1( p 1) mod ps 1( p 1)

n | ind a .

Тогда

n

ind a n

a gind a

g

n mod 2 ps ,

т. е.

существует

решение

xn a mod 2 ps .

ps , где g – имеем

имеем

сравнения

3.2. Задачи для самостоятельного решения

1.Показать существование чисел, относящихся по модулю n к простому делителю функции Эйлера (n) как к показателю, где n = p, n = p k или n = 2p k (p — простое нечетное число, k — натуральное число).

2.Доказать, что квадратичный вычет по простому модулю не является первообразным корнем по этому же модулю.

3.Пусть все отличные от 1 квадратичные вычеты по простому модулю p относятся по mod p к одному и тому же простому показателю q. Доказать,

что p = 2q + 1.

4.Найти число, относящееся по простому модулю p к показателю и одновременно являющееся квадратичным невычетом по этому же модулю, для

83

mod p.

случаев а) = 2, p = 23; б) = 7, p = 23; в) = 11, p = 23; г) = 4, p = 29; д)

= 11, p = 67.

5.Доказать, что биномиальный коэффициент Ckp , где p — простое число, при

1 k < p делится на p.

6.Используя метод математической индукции, доказать, что для любого m и простого p, таких что m < p, справедливо равенство m p mod p = m.

7.	Доказать, что для любых	целых	чисел a и b	справедливо равенство
	(a + b) p mod p = (a p + b p ) mod p, где p — простое число.
8.	Пусть a — квадратичный	вычет	по простому	модулю p, причем

p ≡ 3 mod 4. Доказать, что квадратный корень из a может быть вычислен по

p 1

формуле 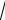a a 4

9. Пусть a — квадратичный вычет по простому модулю p, причем p ≡ 7 mod 8. Доказать, что квадратный корень из a может быть вычислен по

p 1

формуле 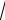a a 4 mod p.

10. Найти число, относящееся к показателю одновременно по простому модулю q и по простому модулю p (рассмотреть случай выполнения условий | q 1 и | p 1, причем 2 не делит ни одно из чисел q 1 и p 1).

11. Найти число, относящееся к показателю одновременно по простому модулю q и по простому модулю p (рассмотреть случай выполнения условий s | p 1 и s | q 1, где s есть значение степени числа в разложении обоих чисел p 1 и q 1).

12. Найти число, относящееся по простому модулю p к показателю и одновременно относящееся по простому модулю q к показателю , в случае выполнения следующих условий НОД ( , q 1) = 1 и НОД ( , p 1) = 1.

13.Показать способ нахождения числа, относящегося к числу как к пока-

зателю по модулю p ( | p 1) и к числу как к показателю по модулю q ( | q 1). Рассмотреть следующий случай: p и q — числа, для которых НОД(p, q) = 1, НОД( , ) = 1, НОД( , q 1) = 1 и НОД( , p 1) = 1.

84

14.Пусть известно разложение числа p 1, где p есть большое простое число размера 1024 бит, причем в разложении имеется простой множительразмера 160 бит. Указать вычислительно эффективный способ нахождения числа , относящегося к показателю .

15.Пусть известно разложение числа p 1, где p есть большое простое число. Указать вычислительно эффективный способ нахождения числа ,

относящегося к показателю = d1d2d3 (произведение трех простых делите-

лей числа p 1).

16.Доказать, что первообразные корни по простому модулю являются квадратичными невычетами по этому же модулю.

17.Известно, что первообразные корни по простому модулю являются квадратичными невычетами по этому же модулю. Верно ли обратное утверждение?

18.Доказать, что первообразный корень по простому модулю p ≥ 3 является квадратичным невычетом степени n | p – 1.

19.Пусть известно разложение числа p 1, где p есть простое число. Как проверить то, что число является первообразным корнем?

20.Для числа , относящегося к простому показателю по простому мо-

дулю	p,	имеется		различных	чисел
{ 1, 2 mod p, 3 mod p, …, mod p = 1}. Доказать, что все эти					числа
относятся по модулю p к показателю .

21.Пусть число есть первообразный корень по простому модулю p. До-

казать, что число 1 mod p также является первообразным корнем по модулю p.

22.Числа и относятся по модулю n к простым показателям и , соот-

ветственно. Доказать, что для всех i {1, 2, …, 1} и

j

{1, 2, …, 1} числа i j относятся по mod n к показателю = .

23.Пусть некоторое число есть показатель по модулю n. Доказать, что любой простой делитель числа является показателем по модулю n.

85

24.Пусть некоторое число есть показатель по модулю n и некоторый делитель числа представим в виде произведения двух простых чисел:= . Доказать, что является показателем по модулю n.

25.Пусть некоторое число есть показатель по модулю n и некоторый делитель числа представим в виде произведения нескольких простых чисел: = … . Доказать, что является показателем по модулю n.

26.Пусть некоторое число есть показатель по модулю n и некоторый делитель числа представим в виде = k, где — простое число, k — натуральное число. Доказать, что является показателем по модулю n.

27.Пусть некоторое число есть показатель по модулю n и есть некоторый делитель числа . Доказать, что является показателем по модулю n.

28.Показать, что если число a bL(m) / mod m 1, где есть некоторый делитель обобщенной функции Эйлера L(m), относится к показателю по модулю m = pq, причем входит в каноническое разложение чисел φ (p) и

φ(q) в степени s и t < s соответственно, то a ≡ 1 mod q.

29.Доказать следующее утверждение: если существует двукратный перво-

образный корень по mod p и по mod q , то обобщенная функция Эйлера числа p q есть показатель по mod (p q ).

30.Найти число, являющееся одновременно первообразным корнем по mod p и по mod q .

31.Для любых ли значений чисел m, n, | φ (m) и | φ (n) можно найти чис-

ло x, относящееся к числам и как к показателям по модулю m и модулю

n соответственно?

32.Предложить вычислительно эффективный способ нахождения числа x, относящегося к числам и как к показателям по mod p и по mod q, где p

и q — простые числа, | p 1 и | q 1.

33.Оценить верхнюю границу мощности множества чисел {x: 1 < x < pq}, относящихся к числам и как к показателям по mod p и по mod q, где p и

q — простые числа, | p 1 и | q 1.

86

34.Пусть требуется найти число , относящееся по модулю p к показателю, длина которого существенно меньше длины p, и одновременно являющееся первообразным корнем по простому модулю q. Предложите вычислительно эффективный способ решения этой задачи.

35.Пусть требуется найти число , относящееся по модулю p к показателю, длина которого существенно меньше длины p, и одновременно являющееся квадратичным вычетом по модулю q. Предложите вычислительно эффективный способ решения этой задачи.

36.Пусть p и q — простые числа и есть число, относящееся к простому показателю по модулю pq. Тогда имеем 1 mod (pq) 1 mod p и

1 mod q. Очевидно, что может иметь место случай, когда делит

только одно из чисел p – 1 и q – 1. Объясните, почему в этом случае не может быть показателем одного из чисел.

37.Пусть требуется найти число , относящееся по простому модулю p к показателю , длина которого существенно меньше длины p, и одновременно являющееся квадратичным невычетом по RSA-модулю n = pq. Предложите вычислительно эффективный способ решения этой задачи.

38.Найти натуральное число , относящееся к простому показателю по модулю p и по модулю q, где p и q — простые числа, причем входит в

каноническое разложение чисел p 1 и q 1 в одинаковой степени s ≥ 1 и

	p 1				q 1				1.
НОД				,
	2	s			2	s

39. Показать, что не существует числа , относящегося к простому показателю по модулю p и по модулю q, где p и q — простые числа, если входит в каноническое разложение чисел p 1 и q 1 в различной степени.

40.Для числа < p, относящегося к показателю по простому модулю p,

имеется различных чисел { 1, 2 mod p, 3 mod p, …, mod p = 1},

для которых при любом i < имеем ( i) = ( )i 1 mod p. Относятся ли все эти числа к показателю ? Содержатся ли среди этих чисел все числа, относящиеся к показателю ? Содержатся ли среди них числа, не относящиеся к показателю ?

87

41.Доказать, что индексы первообразных корней по простому модулю есть числа, взаимно простые с числом p 1.

42.Доказать следующее утверждение. Если НОД (z, p 1) 1, где p —

простое число (p > 2) и z — индекс некоторого числа a < p 1 (т. е. z =

=ind a), то a не является первообразным корнем.

43.Доказать, что при любом основании g индекс i (по простому модулю p)

числа a удовлетворяет соотношению НОД (i, p – 1) = d, где число d не зависит от g.

44. Найти количество классов по простому модулю p, индекс которых удовлетворяет условию НОД (i, p – 1) = d, где d есть некоторый делитель числа p 1.

45.Сколько имеется различных первообразных корней по простому модулю p?

46.Доказать, что любое число i, такое что НОД (i, p – 1) = 1, является индексом первообразного корня.

47.Число a (a mod p ≠ 1) относится по простому модулю p к простому показателю . Доказать, что индекс i числа a (по модулю p) удовлетворяет

условию НОД (i, p 1) p 1.

48. Число a (a mod p ≠ 1) относится по простому модулю p к показателю . Доказать, что индекс i числа a (по модулю p) удовлетворяет условию НОД (i, p 1) p 1.

49. Индекс i (по простому модулю p) числа a (a mod p ≠ 1) удовлетворяет условию НОД (i, p 1) p 1. Показать, что число a относится к показателю

.

50. Индекс некоторого числа g является взаимно простым с p – 1, где p есть простое число. Доказать, что g есть первообразный корень по модулю p.

88

51.Пусть число a относится по простому модулю p к показателю . Дока-

p 1

зать, что a представимо в виде a b mod p.

52.Тест на простоту числа p состоит в проверке выполнимости соотноше-

ния a (n) = 1 mod n, где n = pq и q — заведомо простое число. Показать, что этот тест является эквивалентным тесту Ферма по отношению к числам Кармайкла.

53.Дано значение модуля. Как найти число, относящееся к заданному составному показателю по этому модулю?

54.Вычислить число первообразных корней по модулям 67; 47; 97; 131.

55.Определить количество чисел, относящихся к показателю 2 по модулям

67; 47; 97; 131.

56.Определить количество чисел, относящихся к показателю 11 по моду-

лям 23; 67; 133.

57.Оценить вероятность того, что случайно выбранное число a < p окажется первообразным корнем по модулю p.

58.Указать все показатели по модулям 17, 196 и 625.

59.Указать все показатели по модулю n = 3 5 129 257.

60.Оценить вероятность случайного выбора числа a < p, где p — простое число, относящегося к делителю | p 1 как к показателю.

61.Оценить вероятность того, что для случайного числа (1 < < p) будет выполняться сравнение (p 1)/ mod p 1 (это вероятность генерации чис-

ла, относящегося к показателю ), где p = 2 rq + 1, причем , r и q — простые числа.

62.Пусть g — первообразный корень по простому модулю p. Показать, что

для любого числа a < p 1, взаимно простого с p 1, и любого делителя

p 1

числа p 1 выполняется условие (g a )

mod p 1.

63.Пусть простой модуль p представим в виде p = 4k + 1. Показать, что ес-

ли число a является квадратичным вычетом (невычетом), то число p a является квадратичным вычетом (невычетом).

89

64.Пусть простой модуль p представим в виде p = 4k + 3. Показать, что ес-

ли число a является квадратичным вычетом (невычетом), то число p a является квадратичным невычетом (вычетом).

65.Чему равен наибольший общий делитель двух последовательных натуральных чисел n и n + 1? Объясните почему.

66.Показать, что при любом простом p число p делит число 2 p – 2.

67.Показать, что для любого натурального n > 2 функция Эйлера (n) принимает четные значения.

68.Чему равна вероятность случайного выбора двух целых чисел, которые делятся на заданное число d ?

69.Пусть вероятность случайного выбора двух взаимно простых нату-

ральных чисел a и b равна P Pr[gcd(a,b) 1]. Определите вероятность Pd Pr[gcd(a,b) d ] случайного выбора двух чисел, наибольший общий делитель которых равен d.

				2
70.	Используя равенство	1		, вычислите вероятность случайного
	i 1 i2		6
выбора двух чисел a и b, таких что НОД (a, b) = 1.
71.	Доказать, что для простых чисел вида p 2k 1,				где — простое чис-

ло, вероятность случайного выбора числа ( < p), относящегося по модулю p к показателю ( < p 1), не содержащему делитель , равна 1/ .

72.Доказать, что для простых чисел вида p 2ak 1, где a и — простые числа, вероятность случайного выбора числа ( < p), относящегося по модулю p к показателю ( < p 1), не содержащему делитель , равна 1/ .

73.Доказать, что для простых чисел вида p 2u 1, где u и — простые числа, вероятность случайного выбора числа ( < p), относящегося по

модулю p к показателю ( < p 1), не содержащему делитель , равна 1/ .

74. Доказать, что для простых чисел вида p 2k r 1, где r и — простые числа, вероятность случайного выбора числа ( < p), относящегося по модулю p к показателю ( < p 1), не содержащему делитель , равна 1/ .

90