АГ Векторная алгебра 2015-16 / 01 Векторы и линейные операции над ними

11

1. . Векторы и линейные операции над ними

1. Определения вектора и способы его задания

Луч – часть прямой, ограниченная одной точкой, называемой началом луча.

Определение 1

Два луча плоскости называются сонаправленными, если выполняется одно из условий:

1. лучи лежат на параллельных прямых, и если через начало лучей провести прямую, то оба луча будут лежать по одну сторону от этой прямой в их общей плоскости;

2. если лучи лежат на одной прямой, то один луч является частью другого.

Определение 2

Два луча плоскости называются противоположно направленными, если выполняется одно из условий:

1. лучи лежат на параллельных прямых, и если через начало лучей провести прямую, то оба луча будут лежать по разные стороны от этой прямой;

2. если лучи лежат на одной прямой, то ни один луч не является частью другого.

Определение 3

Множество сонаправленных лучей – это направление на плоскости.

Определение 4

Два луча пространства называются сонаправленными, если выполняется одно из условий:

1. эти лучи лежат на параллельных прямых и если через начало лучей провести плоскость, не содержащую этих лучей, то оба луча будут расположены по одну сторону от этой плоскости;

2. если лучи лежат на одной прямой, то один луч является частью другого.

Определение 5

Два луча пространства называются противоположно направленными, если выполняется одно из условий:

1. лучи лежат на параллельных прямых и если через начало лучей провести плоскость, не содержащую этих лучей, то оба луча будут лежать по разные стороны от этой плоскости;

2. если лучи лежат на одной прямой, то ни один луч не является частью другого.

Определение 6

Множество всех сонаправленных лучей пространства – направление пространства.

Определение 7

Вектор - направленный отрезок, имеющий начало и конец.

Определение 8

Вектор - упорядоченная пара точек, т.е. пара точек, одна из которых является первой (), другая – второй (). Обозначение -.

Определение 9

Луч называется соотнесённым с данным вектором, если начало этого луча совпадает с началом вектора и конец вектора лежит на продолжении этого луча.

Луч, соотнесённый с вектором:

Определение 10

Направление вектора – направление соотнесённого с ним луча.

Определение 11

Длина вектора - расстояние между началом и концом этого вектора.

Чтобы задать вектор, нужно задать:

• начало,

• направление (соотнесённый луч),

• длину.

Определение 12

Равные векторы - векторы, имеющие одинаковые длины и одинаковые направления, но при этом векторы не обязаны совпадать.

Длина вектора обозначается .

Утверждение 1 (Критерий равенства двух векторов)

Два вектора равны тогда и только тогда, когда четырёхугольник, построенный на данных векторах, является параллелограммом.

ABDC – параллелограмм.

B D

A C

Определение 13

Множество всех равных между собой векторов называется свободным вектором ( – обозначение).

Прикладываем вектор к точке A: , тогда вектор называется приложенным к точке A.

Длина вектора обозначается .

Определение 14

Два вектора называются коллинеарными, если они лежат на одной или параллельных прямых.

Определение 15

Три и более векторов называются компланарными, если эти векторы лежат в одной или параллельных плоскостях.

2. Сложение векторов, свойства сложения

Определение 16

Операция сложения

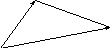
Правило треугольника. Говорят, что

, (1)

если будучи приложенным к началу вектора , его конец будет совпадать с концом , причём конец совпадает с началом .

B

C

A

Свойства операции сложения векторов

1. Коммутативность

(2)

B

A

D

Дано:

Доказать: , то есть .

 По правилу треугольника и

Пусть точки и не совпадут, то есть .

Если , то- параллелограмм по признаку равенства векторов (Утверждение 1).

и , но , тогда и 

Правило параллелограмма.

Приложим векторы и к точке A и достроим до параллелограмма. Тогда сумма – вектор, совпадающий с диагональю параллелограмма, с началом в точке A.

A

2. Ассоциативность

(3)

B C

A D

 , 

Правило сложения n векторов

Определение 17

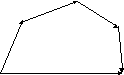
Сложить n векторов можно так: с помощью параллельного переноса перемещаем второй вектор так, чтобы его начало совпадало с концом первого, затем начало третьего совмещаем с концом второго и т. д. по аналогии. Затем начало последнего - с концом предпоследнего. Тогда вектор, начало которого совпадает с началом первого, а конец - с концом последнего, и будет искомой суммой n векторов.

n = 4

3. Нулевой вектор

(4)

 по правилу треугольника



Определение 18

Нулевой вектор есть пара совпадающих точек.

Утверждение 2

Нулевой вектор коллинеарен любому вектору, компланарен любой паре векторов.

4. Противоположный вектор

(5)

где - противоположный к .

 Пусть ,

тогда по правилу треугольника.

Проверка: . 

Обозначение:

Определение 19

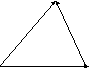
Операция вычитания

Говорят, что

, (6)

если будучи приложенным к концу вектора , его конец будет совпадать с концом _, причём начало совпадает с началом .

B

A C

3. Умножение вектора на число, свойства умножения

Определение 20

Операция умножения вектора на число

Пусть задан вектор и . Тогда

, (7)

если:

1. 

2. 

3. , .

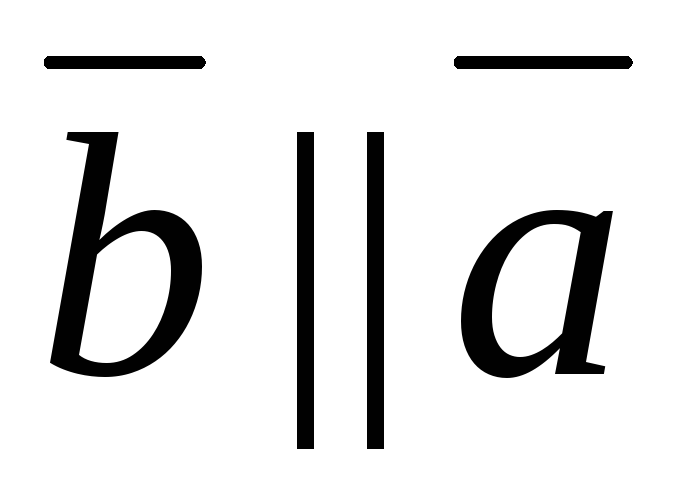
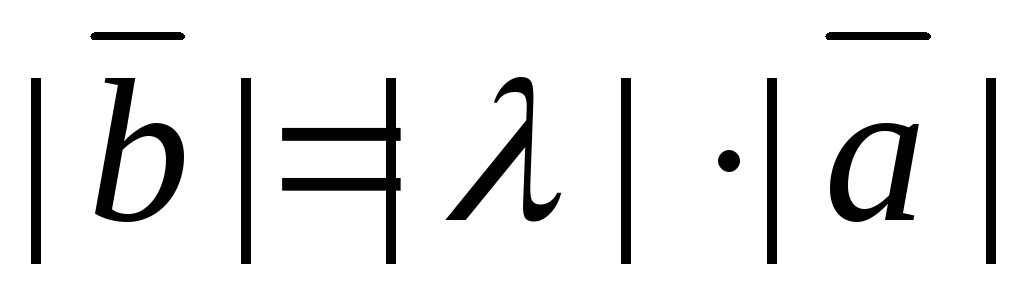
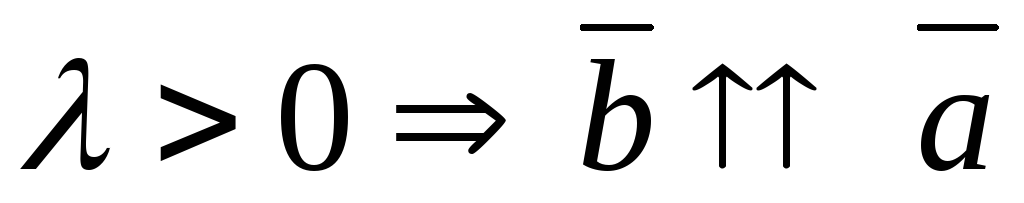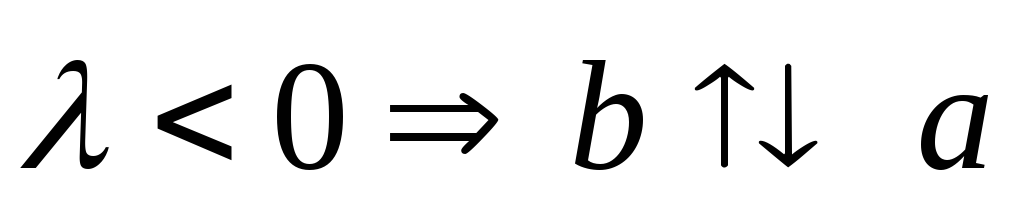Свойства операции умножения вектора на число

5. Дистрибутивность относительно сложения векторов.

(8)

 I. не коллинеарен _{, ,} .

ABDC – параллелограмм, построенный на векторах и .

Пусть ,

_B`

_B

_A D D`

_C

_C`

AB`D`C` - параллелограмм, построенный на векторах и - подобен параллелограмму ABDC с коэффициентом подобия .

AB`D’C` - параллелограмм

( – докажите самостоятельно)

II. коллинеарен _,, .

S

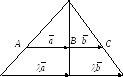
A` B’ C`

(по двум углам), т.к. , то коэффициент подобия равен .

(по двум углам) .

(по двум углам), т.к. , то коэффициент подобия равен

В остальных случаях рассуждения аналогичны. 

6. Дистрибутивность относительно сложения чисел.

(9)

Возможны следующие случаи:





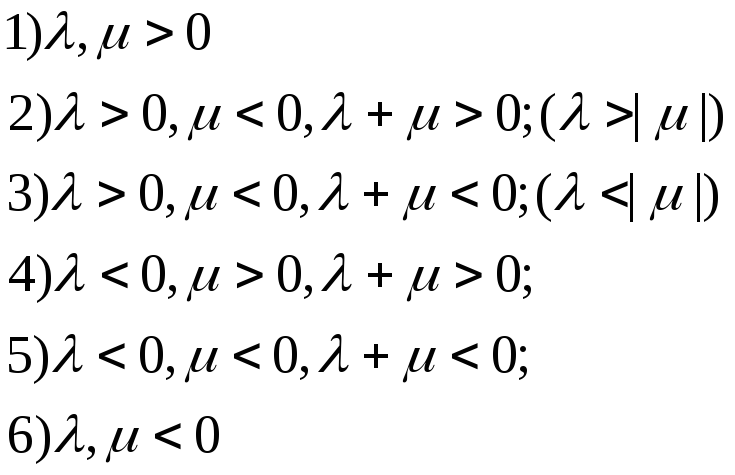
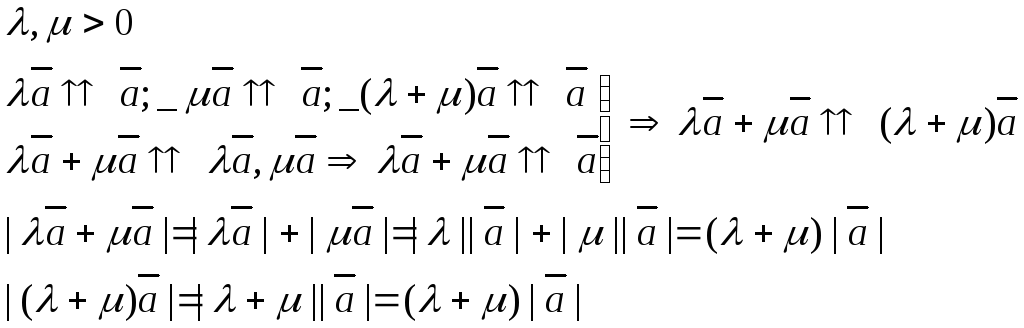
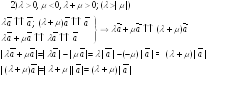
7. Ассоциативность умножения вектора на число

(10)



1. 

2. 



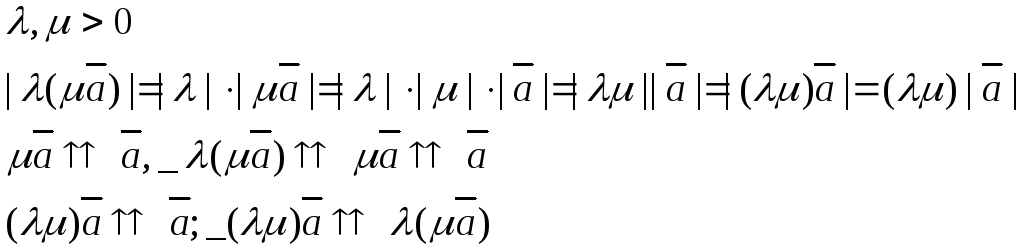
Теорема 1

Для того чтобы .

 Необходимость:

Пусть . Если , то ;

Если , то ;

_{Достаточность:}

Если , то по определению умножения вектора на число эти векторы коллинеарны. 

4. Векторное пространство

Определение 21

Векторное пространство – произвольное множество элементов (векторов), на котором введены операции сложения элементов и умножения на число из R, удовлетворяющие 8 аксиомам:

1. Коммутативность

2. Ассоциативность

3. Существование нуля

4. Существование противоположного элемента

5. Дистрибутивность относительно сложения векторов

6. Дистрибутивность относительно сложения чисел

7. Ассоциативность умножения вектора на число

8. Умножение на единицу

Примеры векторных пространств

Примером векторных пространств могут служить: плоскость – двумерное векторное пространство, прямая – одномерное векторное пространство.