
Методы и средства передачи информации (Лекция №12)
.pdf
Методы и средства передачи
 информации
информации
Лекционный курс
Лекция № 12
Содержание
1.Алгоритм расчета первичных параметров линий передачи на переменном токе. Поверхностный эффект
2.Первичные и вторичные параметры линий передачи с учетом поверхностного эффекта
3.Особенности моделей длинных линий односвязных структур линий передачи
1.Алгоритм расчета первичных параметров линий передачи на переменном токе. Поверхностный эффект
В случае переменных полей возникает неравномерность распределения переменного поля (или тока в соответствии с дифференциальным законом Ома: J = σE ) по сечению в проводящих средах (в частности в проводах и стенках линий передачи). Это приводит к тому, что центральная часть провода (или проводника), по которому проходит переменный ток, используется хуже, чем сечение провода при прохождении постоянного тока. Это приводит к возрастанию сопротивления провода по сравнению с его сопротивлением постоянному току. Одновременно должна уменьшаться индуктивность провода против индуктивности, вычисленной при равномерном распределении тока по сечению. Кроме того, близость проводов с токами или других проводящих тел (металлических элементов крепления, стенок корпусов блоков, проводящих экранов) также влияет на распределение плотности тока по сечению провода. Это явление называется «эффектом близости». Эффект возникает вследствие связи между векторами поля. Так, например, плотность тока выше в тех частях сечений проводов, где больше напряженность магнитного поля. Поэтому в случае параллельных проводов с токами противоположного направления плотность тока будет большей в частях их сечений наиболее близких друг к другу, а в случае одинаково направленных токов в проводах – наоборот (см. рис.12.1).

1 |
|
• |
H2 |
|
|
2 |
1 |
2 |
|
|
|
H 2 |
|
|
|
H1 |
а) |
H1 |
|
|
|
б) |
|
Рисунок 12.1− К пояснению эффекта «близости»
Процесс распространения гармонических волн в проводящих средах сопровождается постепенным уменьшением амплитуд векторов напряженностей электрического и магнитного полей и плотности тока проводимости, связанных между собой уравнениями поля. Этот эффект наблюдается при распространении волны от поверхности проводника вглубь него. По этой причине эффект называется поверхностным, или скин-эффектом. Наш интерес к изучению поверхностного эффекта в основном связан с вопросами распределения поля (и плотности тока) в проводах и проводящих поверхностях стенок линий передачи. Тем не менее, мв рассмотрим явление несколько шире, с тем, чтобы в дальнейшем изучении курса иметь возможность оперировать веденными здесь понятиями.
Теперь рассмотрим эти явления с применением методов теории поля. Начнем анализ с рассмотрения явлений связанных с процессами, возникающими при распространении плоской гармонической волны в проводящей среде.
Пусть однородная плоская гармоническая волна проникает в проводник с электрофизическими параметрами σ ; µ r = const через его плоскую поверх-
ность z = 0 (рис. 12.2), параллельную волновым (фазовым) плоскостям. Пусть проводник занимает всё полупространство. Пусть на поверхности проводника задано значение комплексной амплитуды одного из векторов поля волны, например H ym
вать в виде тока, что и будет сделано при дальнейшем рассмотрении.
Пусть требуется найти распределение комплексных амплитуд векторов J, E и H в проводнике.
2
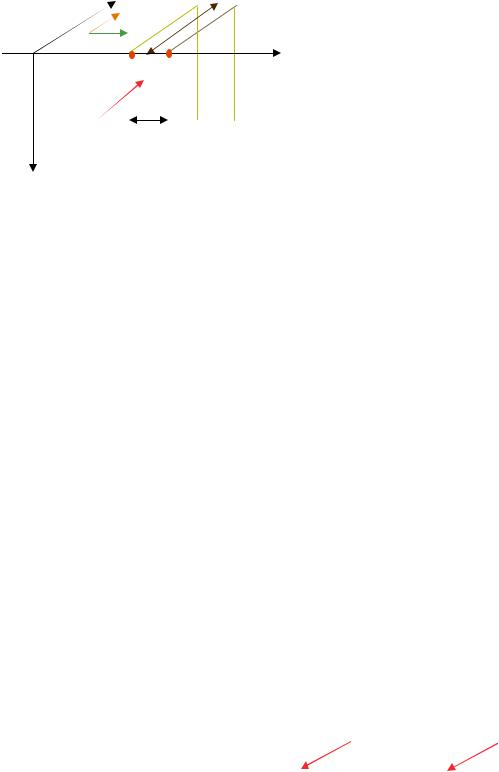
x |
Eх |
|
|
|
|
|
|
||
|
|
|
|
|
|
Рисунок 12.2 − Модель расчета |
|||
σ = 0 |
|
|
Ну |
|
|
h |
|
|
|
|
|
|
|
|
|
y векторов поля при учете поверх- |
|||
|
|
|
|
|
|
||||
σ≠ 0 |
m |
|
I |
|
n |
|
ностного эффекта |
||
|
|
||||||||
|
|
|
|
|
|
|
|
||
|
|
|
a |
|
|
|
|
|
|
z |
|
|
∞ |
|
∞ |
|
|
||
|
|
|
|
|
|||||
Обратимся к уравнениям Максвелла в частотной области для проводящей среды в пренебрежении токами смещения в сравнении с токами проводимости :
rot H m = J m , |
(12.1) |
rot E m = − jωµ a H m , |
(12.2) |
div H m = 0 ;
div J m = div rot H m = [ , H ]= 0 ;
Так как в рассматриваемом случае вектор Н имеет только одну состаляющую, зависящую только от координаты z , то уравнение (12.1) в декартовой прямоугольной системе координат примет вид:
|
|
x 0 y 0 |
z 0 |
|
|
∂ |
|
|
|||||
|
|
|
∂ |
|
∂ ∂ |
|
= x 0 |
H ym = x 0 |
J xm + 0 + 0 , |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
∂x ∂y |
|
∂z |
∂z |
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
0 |
H ym |
0 |
|
|
|
|
|
||||
или |
− d H ym / dz = J xm , |
|
(12.3) |
||||||||||
а уравнение (12.2), умноженное на постоянную проводимости σ, с учетом (12.3) записывается в виде
− jσµa H m =x 0 |
0 +y 0 (− jσµa H ym )+z 0 |
0 =rot x E m +rot y E m +rot z E m = rot y E m = |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
x 0 |
y 0 z 0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
∂ ∂ ∂ |
|
= y 0 |
∂ |
σ E xm |
= y 0 |
∂ |
|
J xm , |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
∂x |
|
|
∂y ∂z |
∂z |
∂z |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
σ E xm |
0 0 |
|
|
|
|
|
|
|
|
|
|||||
3

где учтено, что, если составляющая ротора равна нулю, то равны нулю соответственные составляющие вектора в его определителе.
Итак, получаем
∂ J xm |
|
|
|
|
|
= −µ a σ H ym = − jωµ 0 |
µ 0 |
σ H ym . |
(12.4) |
|
||||
∂z |
|
|
|
|
Выражение (12.4) принято записывать с применением обозначений:
π
p = +  jωµ0µr σ = +
jωµ0µr σ = +  ωµ0µr σ e j 4 = +
ωµ0µr σ e j 4 = + ωµ0µr σ e j 450 =
ωµ0µr σ e j 450 =
= 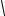 12 ωµ 0 µ r σ + j
12 ωµ 0 µ r σ + j  12 ωµ 0 µ r σ =b + jb ,
12 ωµ 0 µ r σ =b + jb ,
где b = |
1 |
ωµ 0 µ r σ . |
|
2 |
|
Введенное обозначение имеет физический смысл, который выявится при дальнейшем анализе.
С учетом данных обозначений выражение (12.4) запишется в виде
|
|
∂ J xm |
= − p |
2 |
H ym . |
(12.5) |
|
|
|
∂z |
|
||||
|
|
|
|
|
|
|
|
Из уравнения (12.5) с подстановкой выражения (123.3) получается диффе- |
|||||||
ренциальное уравнение для составляющей H ym |
вектора Н в частотной области: |
||||||
|
∂ 2 H ym |
= p 2 |
H ym . |
(12.6) |
|||
|
|
|
|
||||
|
|
∂z 2 |
|
||||
|
|
|
|
|
|
|
|
Уравнение (12.6) является обыкновенным дифференциальным уравнением второго порядка и его решением является функция
H ym |
=C 1 e − pz |
+C 2 e + pz , |
(12.7) |
где C 1 =C 1 e jΨ1 и C 2 |
=C 2 e jΨ2 |
– постоянные интегрирования, подлежащие |
|
определению из граничных условий.
Физический смысл полученного решения следует из анализа выражения для мгновенных значений напряженности магнитного поля Н
4

H y ( t ) =C 1 e − bz |
sin( ωt −bz + Ψ1 |
) +C 2 e − bz sin( ωt +bz + Ψ2 ). |
(12.8) |
||
Первое слагаемое в формуле (12.8) определяет бегущую волну, распро- |
|||||
страняющуюся |
в направлении возрастающих значений z (вглубь проводника) с |
||||
фазовой скоростью |
|
|
|
|
|
v = dz / dt = ω/ b = |
2 ω/ µ 0 µ r σ , |
|
(12.9) |
||
зависящей от частоты, и с длиной волны |
|
||||
λ = 2 π = |
2 π |
= |
2 π |
2 . |
(12.10) |
b |
ω/ 2µ 0 µ r σ |
ω/ µ 0 µ r σ |
|
||
По мере перемещения волны вглубь проводника её амплитуды (и Е и Н) затухают по экспоненциальному закону и на расстоянии z = λ от поверхности уменьшается в e bλ =e 2 π ≈540 раз.
Второе слагаемое в формуле (12.8) представляет встречную волну, амплитуда которой также затухает по мере перемещения волны. Для однородного проводника неограниченной глубины источник образования обратной волны отсутствует, поэтому постоянную интегрирования C 2 следует принять равной ну-
лю. При этом решение принимает вид |
|
H ym =C 1 e − pz . |
(12.11) |
Постоянную C 1находим из граничного условия на поверхности проводни- |
|
ка. Полагая при z = 0 значение H ym |
= H ym (0) , получаем |
C 1 = H ym ( 0 ). |
(12.12) |
Практически, удобнее заменить это условие другим, связав H ym (0)с током.
Для этого достаточно мысленно разбить весь проводник на отдельные тонкие слои, один из которых с толщиной а показан на рис. 12.2. Пусть известна ком-
плексная амплитуда тока I m , распределенного по сечению ∞ – m – n – ∞ этого слоя. Применим закон полного тока:
∫Hdl = I xm
5

к замкнутому контуру ∞ – m – n – ∞. При этом весь интеграл сведется к произведению H ym (0) a , так как на вертикальных сторонах контура вектора Н и dl
взаимно ортогональны и их скалярное произведение равно нулю, а на нижней стороне контура, лежащей в бесконечности, H ym (∞) =0. Таким образом,
H ym (0) a = I m , или H ym (0) = |
|
I |
m |
|
|
. Откуда постоянная C 1 |
=H ym ( 0 ) =I m / a . |
|||||||||||||||||
|
|
a |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив найденное значение |
C 1в формулу (12.11), |
находим искомые |
||||||||||||||||||||||
векторы поля: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H ym |
= |
|
|
I |
m |
|
e |
−pz |
; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
J xm |
= |
|
|
p I m |
|
|
e −pz |
= |
|
|
p I m |
e −bz e − jbz ; |
(12.13) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
a |
|
|
|
|
|
|
a |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
E xm |
= |
|
|
J |
xm |
|
= |
|
p I |
m |
|
e −bz e − jbz . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
σ |
|
|
|
aσ |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Важно заметить, что отношение напряженностей поля |
|
|||||||||||||||||||||||
E xm |
= |
|
|
p |
= |
|
|
|
ωµ 0 µ r |
e |
+ j 45 0 |
|
||||||||||||
H ym |
|
|
σ |
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
одинаково для всех |
точек |
|
проводника и зависит только от параметров среды |
|||||||||||||||||||||
и частоты. Оно имеет размерность сопротивления и рассматривается как волновое комплексное сопротивление проводника
Z в |
= |
ωµ 0 µ r |
e |
+ j 45 |
0 |
(12.14) |
σ |
|
, |
||||
|
|
|
|
|
|
имеющее индуктивный характер.
Рассмотрим следствия из полученных результатов.
Воспользуемся теоремой Умова-Пойнтинга в комплексной форме и найдем активное сопротивление слоя длиной h (параллелепипед бесконечной глубины, у которого верхнее основание образуют стороны а и h, рис. 12.2):
6

− ∫ |
1 |
|
|
|
1 |
2 |
( r + jωL ). |
2 |
E,H ds = |
2 |
I m |
||||
S |
|
|
|
|
|
||
В нашем случае вектор Пойнтинга направлен по оси z и поток его отличен от нуля только на верхнем основании проводника (z = 0), так как на остальных
поверхностях векторы |
|
|
|
и ds взаимно ортогональны. Тогда поток векто- |
||||||||||||||
E ,H |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ра Пойнтинга, направленный вглубь проводника через площадь поверхности S = |
||||||||||||||||||
а · h равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
I m |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
I m |
|
|
1 |
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ah = |
|
|
I m |
( r + jωL ), |
||||
2 |
|
|
aσ |
|
a |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 ( b + jb ) h |
|
1 |
2 |
|
|
|
|
|||||||
|
I m |
|
|
|
|
|
= |
|
|
I m |
|
( r + jωL ). |
||||||
2 |
|
|
aσ |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
Приравнивая действительные части получаем |
||||||||||||||||||
I 2 r = I |
2 hb |
= I 2 |
|
h |
|
и r = |
h |
. |
||||||||||
|
aσ |
aσ1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
aσ1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
Этот результат показывает, что активная мощность, выделяемая в толще проводника переменным током с действующим значением I, равна мощности, которую выделил бы постоянный ток того же значения I в проводнике той же длины h и проводимости σ, но с сечением, имеющим ту же ширину а и высоту b. Величину
1 |
= |
2 |
(12.15) |
||
|
|
b |
|
ωµ 0 µ r σ |
|
называют |
|
|
|
||
глубиной проникновения (тока или поля) |
или толщиной поверхно- |
||||
|
. |
|
|
|
|
стного слоя, или скинслоем |
|
|
|
||
Из уравнения (12.13) следует, что на этой глубине амплитуда плотности тока (и остальных векторов) уменьшается в е = 2,718 раза по сравнению с её зна-
7

чением на поверхности проводника. Так как λ=2π/b, то глубина проникновения в 2π раз меньше длины волны в проводнике.
Из формулы (12.15) видно, что глубина проникновения уменьшается с увеличением частоты, магнитной проницаемости и проводимости материала. Так, например, при частоте f = 50 Гц глубина проникновения равна: в меди
( σ =5 , 8 10 7 См/м) 9,4 мм, в стали ( σ =1 10 7 См/м; µ r =1000 ) 0,74 мм (за счет магнитной проницаемости стали). При частоте f = 500 000 Гц глубина проникно-
вения уменьшается в 500000/ 50 =100раз. В идеальный проводник ( σ=∞См/м )
500000/ 50 =100раз. В идеальный проводник ( σ=∞См/м )
поле не проникает, оно полностью отражается от него, а ток проводимости становится поверхностным.
Заметим, что несмотря на то, что выражение (12.15) получено для проводника с плоской поверхностью, в практических задачах оно пригодно для вычисления потерь мощности в проводниках, имеющих криволинейную поверхность, если радиус кривизны значительно превышает глубину проникновения.
Из обширного числа инженерных задач, использующих при создании технических устройств явление поверхностного эффекта, основная область интереса к этому явлению в основном ограничена задачами рационального построения экранов в электромагнитном поле, о чем мы будем говорить во второй части нашего курса. Ориентируясь на эту, ожидаемую в следующем семестре, задачу, и, одновременно, для полного понимания процессов в электродинамической системе, образованной проводящим и диэлектрическим полупространствами, разделенными плоской границей раздела, проведем рассчет поле в диэлектрике.
Пусть плоская электромагнитная волна, параметры которой на границе раздела соответствуют предыдущему случаю (см. рис. 12.2) приходит к границе раздела от источника в диэлектрической среде. Тогда, в любых точках наблюдения в диэлектрике электрическую и магнитную составляющие поля можно записать в виде суммы прямой (падающей на границу раздела сред) и обратной (отраженной от границы раздела) волн:
8

H = H пад e − jkz |
+ H отр e + jkz |
|
|
|
|
|
|
|
|
|
(при z ≤ 0 ), |
|
|
|
|
Е= Z в0 (H пад |
e − jkz − H отр e + jkz |
|
|
) |
|
||
|
|
|
|
где H пад |
и H отр |
– векторы на границе раздела (z = 0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
k = ω/ v = ω |
ε 0 ε r |
µ 0 µ r |
|
– постоянная распространения в диэлектрике; |
||||||||||||||||||||||||||||||||||||||||
Z в0 = |
|
µ 0 |
|
µ r |
– волновое сопротивление в диэлектрике. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
ε 0 |
ε r |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из граничных условий H 1 t |
= H 2 t , |
|
E 1 t = E 2 t на поверхности проводника |
|||||||||||||||||||||||||||||||||||||||||
(при z = 0) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
H y |
( 0 ) = H y пад |
|
( 0 ) + H y отр |
( 0 ) = I / a; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
E 1 x |
( 0 ) = Z в0 (H y пад ( 0 ) − H y отр |
|
( 0 ) )= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
= E |
|
( 0 ) = Z |
|
|
H |
|
( 0 ) = Z |
|
|
I |
= |
pI |
|
|
|
jωµ 0 |
µ r |
, |
|
||||||||||||||||||
|
|
|
|
|
|
|
2 x |
|
в |
y |
в |
|
|
= |
|
|
|
|
|
|
|
|
I |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
σa |
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H y пад |
|
|
1 I |
|
|
Z в |
|
I |
Z в0 + Z в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
( 0 ) |
= |
|
|
|
|
1+ |
|
|
= |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 a |
Z в0 |
|
|
|
|
|
2 Z в0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
E x пад |
( 0 ) = Z в0 |
H y пад ( 0 ) = |
|
I |
|
Z в0 + Z в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H y отр |
|
|
|
1 I |
|
|
|
Z в |
|
|
I |
|
Z в0 − Z в |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 0 ) = |
|
|
|
|
1 |
− |
|
|
= |
|
|
|
|
|
|
|
|
|
|
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|
|
2 Z в0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z в0 |
a |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E x отр |
( 0 ) = Z в0 |
H y отр |
|
|
|
|
I |
Z |
в0 − Z |
в |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 0 ) = |
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Интересно заметить, что если принять по аналогии с длинной линией (цепью с распределенными параметрами) коэффициент отражения n на границе раз-
дела в виде n = − |
H y отр |
= − |
Z в0 |
− Z в |
= |
Z в |
− Z в0 |
, то процесс отражения па- |
|
H y пад |
Z в0 |
+ Z в |
Z в0 |
+ Z в |
|||||
|
|
|
|
9

дающей волны в диэлектрике от границы раздела диэлектрик / проводящая среда можно интерпретировать по аналогии с длинной линией, приняв в качест-
ве нагрузки для волны в диэлектрике значение Z в . |
При таком n поля в диэлек- |
||
трике можно представить в виде: |
|
E = E пад (1 + n ) ; |
H = H пад (1 − n ) .Такая ин- |
|
|||
терпретация соответствует замене (или аналогииU): E и I H .
Обратим внимание на числовые данные найденных параметров, характеризующих поверхностный эффект. Это позволит нам перейти к оценке первичных параметров линий передачи. Расчет параметров проведем на примере рассмотрения задач.
Задача 12.1. На поверхности медной пластины (рис. 12.3) возбуждено элек-
трическое поле с напряженностью E ( t ) = E 0 m sinωt , где ω=2 π 10 6 рад/c.
Удельная проводимость меди σ =5 , 6 10 7 Cм/м. Определить параметры,
характеризующие распространение бегущей волны в меди: постоянную распространения, коэффициенты затухания и фазы, условную глубину проникновения, волновое сопротивление, фазовую скорость и длину волны.
x
Е
|
|
П |
|
Рисунок 12.3 − расчетная модель |
v |
z |
|||
|
|
|
к задаче 9.1 |
|
|
|
|
Н
у
Полагая, что E 0 m =  2 мВ/ми что обратная волна отсутствует, записать выражения комплексных напряженностей электрического поля Е и магнитного поля Н в функции расстояния z от поверхности пластины и мгновенных значений Е и Н в функции координаты z и времени. Найти мгновенные значения Н (t) на поверхности пластины, а также Е (t) и Н (t) на расстоянии 0,1 мм от поверхности. Определить выражения плотности тока J (t) на поверхности и на
2 мВ/ми что обратная волна отсутствует, записать выражения комплексных напряженностей электрического поля Е и магнитного поля Н в функции расстояния z от поверхности пластины и мгновенных значений Е и Н в функции координаты z и времени. Найти мгновенные значения Н (t) на поверхности пластины, а также Е (t) и Н (t) на расстоянии 0,1 мм от поверхности. Определить выражения плотности тока J (t) на поверхности и на
10
