Методы и средства передачи информации (Лекция №6)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Теория передачи информации

Файл:

I ( x ) = j

sinβx + I 2

.pdf

Скачиваний:

Добавлен:

13.03.2016

Размер:

578.22 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Методы и средства передачи информации

Лекционный курс

Лекция № 6

Содержание

1.«Неискажающие» длинные линии

2.Длинные линии без потерь

3.Распределения напряжений и токов в длинной линии без потерь в зависимости от нагрузок на концах линии

4.Стоячие волны

5.Согласование длинных линий

1.«Неискажающие» длинные линии

Влекции № 3 было показано, что для неискажающей передаче информационного сигнала (импульса) вдоль согласованной длинной линии необходимо обеспечить постоянство по частоте фазовой скорости v и волнового сопротивления Z B . Этого можно достичь в двух случаях.

1) При равенстве отношений первичных параметров

L 0

, или иначе

g 0

C 0

оно же в виде:

, что приводит к виду фазовой скорости

L 0

v =

L 0 C 0

µ r ε r ,

где с − скорость света в вакууме,

ε r

и µ r − относительные диэлектрическая и

магнитная проницаемости среде распространения волны в линии (в первом приближении, диэлектрик, окружающий проводник линии). Видно, что v не зависит от частоты. Такая линия называется «линией без искажений».

2) При равенствах r0	= 0 и g 0	= 0, что также приводят к
v =	1		c
v =	L 0 C 0	=	µ r ε r .

Такая линия называется линией без потерь и тоже является неискажающей.

Как уже указывалось, это идеальные варианты длинных линий и практически создать ни первую, ни вторую из этих линий невозможно, можно лишь приближаться к их реализации. Причем на практике проще приблизиться к реализации линии без потерь (т.е. минимизировать потери в линиях).

До настоящего времени мы говорили о существовании влияния дисперсии фазовой скорости (т.е., по существу, первичных параметров линии) на форму (искажения) информационного импульса (ИС). Давайте оценим степень влияния первичных параметров длинной линии на форму сигнала и на основе этих данных определим оптимальные свойства линий с наименьшими из допустимых искажений.

Оценку искажений ИС, за счет электрических свойств ЛС также можно рассчитать (или оценить) на основе интегрирования телеграфных уравнений. Однако на практике, для оценки таких искажений удобно использовать приближенные методы.

В основе этих приближенных методов – подвергнутые преобразованию Лапласа решения телеграфных уравнений в гиперболических функциях:

U (p, x) = U	2	(p,l)	ch γ (l − x) + Zc(p) sh
	2					Zн(p)
						Zн(p)
			ch γ (l − x)			sh γ (l − x)
			ch γ (l − x)		+	sh γ (l − x)
I(p, x) = U2(p,l)				Zн(p)	+	Zc(p)
				Zн(p)		Zc(p)

γ (l − x)

, (6.1)

где γ =	(r + p L ) (g			+ pC ) ; Z		=	(r0 + p L0)			, x – расстояние от генератора.
	0	0	0	0	c		(g	0	+ pC )
								0	0

Если на входе ЛС задано напряжение U1(p), а на выходе задана нагрузка

Zн(p) , то решение известно:

				Z c	( p )
	ch γ( l − x ) +					sh γ( l − x )
				Z н	( p )
U ( p , x ) =U 1	( p )						=

		ch γl +		Z c	( p )	sh γl

			Z н		( p )

	Z н	( p ) ch γ( l − x ) + Z c ( p ) sh γ( l − x )
=U 1	( p )		.	(6.2)
		Z н ( p ) ch γl + Z c ( p ) sh γl

Выражение (6.2) позволяет рассчитать ЧХ напряжения в любом сечении x в установившемся режиме. В случае импульсных сигналов необходим переход к временным зависимостям. В основе такого перехода − обратное преобразование Лапласа. В общем случае осуществление этого перехода − сложный процесс, возможный на базе численного анализа.

В случае некоторых идеализированных вариантов ЛС удается получить аналитические решения:

1. ЛС без потерь r0 = g0 = 0

Тогда:

γ = p

L C

p ,

V =

Vф

L C

(p)

(l − x)

(p)

U(p,x) =U (p)

(p)

Vф

Zн(p)

Vф

В согласованном режиме (или при бесконечно длинной ЛС)

Zн(p) = Zс(p) =

С0

(l −x)

(l − x) + sh

− x)

−

eVф

U(p,x) =U (p)

Vф

= =U (p)

=U (p) e

(6.3)

l + sh

Vф

−

Если

(p,0) =

0 , то

U( p,x ) =

(6.4)

0 e ф

и обратное преобразование Лапласа u (x,t) =U0

– функция бегущей вол-

1 t

−

ны напряжения. Это можно показать,

рассмотрев преобразование Лапласа от

единичной функции 1 t −

Действительно,

∞

− p t −

− p

∞

−p

−

Vф

−

∫1(ξ)e

∫1 t −

tdt =

∫1(ξ) e

фdξ =

p ξdξ e

Vф

14243

−

Vф

−p Vф

∞

− p t −

− p

∞

−p

−

Vф

−

∫1(ξ)e

∫1 t −

tdt =

∫1(ξ) e

фdξ =

p ξdξ

142V43ф

−

Vф

−p Vф

но так как 1(ξ) равно 0 при ξ ≤ 0, то последнее выражение можно записать в виде

∞

− p

∞

∫1(ξ)e

− p ξ

Vф

− p ξ

Vф

dξ

Волна тока i (x,t) = u (x,t) может быть найдена из известной связи между

Zс

током и напряжением в плоской волне (закона Ома для волны).

Вывод: прямоугольный (заметим, что и любой иной формы) импульс не искажается при прохождении (передаче) вдоль согласованной линии связи без потерь.

2. ЛС с малыми потерями, которые удовлетворят условиям:

r0 << ωL0 , g0 << ωC0 .

При этом
		r			g	0
γ = p L C		0		+		0		≈
γ = p L C	1+	pL	1	+	pC			≈
0 0		pL			pC
		0				0
≈ p 1+ r0 C0 + g0 L0 + r0 g0							≈ p 1+ r0 C0 + g0 L0 ≈
V	p L C		p2		L C V				p L C
ф	0	0			0 0			ф	0 0

r C + g

≈

2 p L C

≈

2L V 2C V

0 0

0 ф

≈

r L C

L C

+ α,

0 0 +

0 0

0 +

где α – постоянная затухания.

e−

xe−α x на входе

Тогда при единичном ступенчатом сигнале U(p,x) =

Vф

ЛС обратное преобразование Лапласа приводит к выражениям

−α x

u (x,t) = e

1 t

−

(6.5)

u(x,t)

i (x,t)

≈

Из (6.5) следует, что при распространении прямоугольного (или любой другой формы) импульса вдоль такой ЛС его форма не изменяется. Падает лишь амплитуда, согласно выражению U0 e−α x .

3. Увеличение потерь r0 и g0 приводит к существенным дисперсионным

искажениям сигналов, распространяющихся вдоль линии.

Рассмотрим реакцию на прямоугольный импульс свойств RC-линии (тер-

мин для систем, где можно считать g0 ≈ L0 ≈ 0 ).
Тогда	γ =	p r0 C0 и при бесконечной (согласованной) линии, т.						е. при
Zн(p) = ZC =	r0	, реакция на единичную ступеньку запишется в виде:
	pC0
		U(p,x) =	1	e	−x	r C p	.	(6.6)
						0 0
						0 0

Переход от (6.6) к временным функциям дает:

		1
	p	1		,	(6.7)
u(x,t) =1− Ф x r0 C0	p	2		,	(6.7)
		2	t

где Ф(θ)= 2 ∫e−ξ2dξ = erf(θ) – функция ошибок Лапласа.

π 0

Из формулы (6.7) следует, что напряжение и ток в каждой точке x линии возникает мгновенно. Это результат пренебрежения погонной индуктивностью L0 , определяющей конечную скорость распространения Vф волны. Выражение

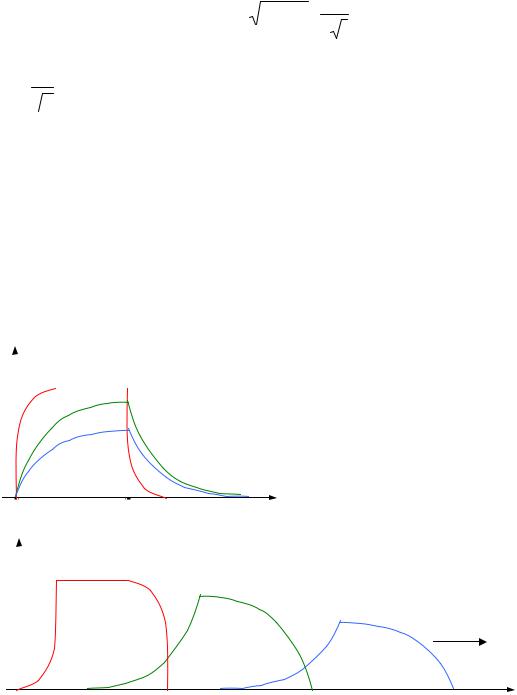
(6.7) показывает, что при распространении волны вдоль линии, форма импульса в каждой точке x изменяется, причем уменьшается амплитуда импульса и импульс расширяется. Качественно это показывает рис. 6.1.

	u( t)

	х1	х2	х1< х2< х3
		х3
			а)	t
				t



	u( x,t)
			t1
				t2
				t3	Vф
					х
					х
			х1= Vф t1	х2= Vф t2	х3= Vф t3
			х1= Vф t1	х2= Vф t2	х3= Vф t3
			б)
Рисунок 6.1 − Кривые u(x,t) в разных сечениях линии:
	а – без учета запаздывания;			б – с учетом запаздывания

Завершая рассмотрение заметим, что к искажениям сигнала приводит также наличие неоднородностей в ЛС (изменение параметров линии, сосредоточен-

ные элементы, включенные в линию, или на её конце, разветвления в линии, и

т.п.).

В заключение заметим, что для цифровых и двухпозиционных сигналов наиболее опасно увеличение времени распространения сигналов и дисперсионное увеличение длительности фронтов импульсов. Это ограничивает допустимые длины отрезков соединительных ЛС, требует включения в рассечки отрезков ЛС усилителей – регенераторов сигнала, а также приводит к необходимости использования стробирования полезного сигнала для повышения достоверности передачи информации.

2. Длинные линии без потерь

Интерес к рассмотрению свойств длинных линий без потерь носит академический характер, так как позволяет упростить процесс анализа явлений в длинных линиях, свойственных и линиям с потерями. Причем, так как уменьшение искажений формы сигналов осуществляется за счет уменьшения значений погонных продольных сопротивлений и поперечных погонных проводимостей, то результаты, полученные для линий без потерь можно применять к линиям с малыми потерями.

Для коротких высокочастотных, линий, применяемых в радиотехнике, электронике и импульсной технике, в том числе и устройствах бол ЭВА, с достаточно большой точностью, приемлемой для инженерных расчетов, можно пренебречь сопротивлением r0 и проводимостью g 0 по сравнению с ωL 0 и ωC 0 . По-

этому в электронной технике очень часто двухпроводные воздушные линии и коаксиальные кабели рассматривают как линии без потерь, т.е. как идеализацию действительной линии.

Для линии без потерь справедливо:

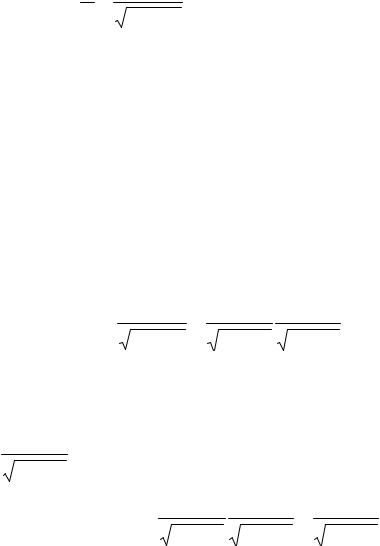
α = 0 ;			β = ω L 0		C 0 ;		Z В = Z В e jθ =	L 0 =Z В; θ = 0;
								C 0
v =	ω	=	1	;	λ =	2 π	,
	β		L 0 C 0			β

т.е. в линии без потерь затухание равно нулю, а волновое сопротивление активное и не зависит от частоты. Точно так же и фазовая скорость в линии без потерь не зависит от частоты. Заметим, что коэффициент фазы β, волновое сопротивле-

ние Z В, фазовая скорость волны v и длина волны λ в линии без потерь такие же как и для неискажающей линии с потерями (см. лекцию №3).

Формулу v =	ω	=	1	для фазовой скорости электромагнитной волны
	β		L 0 C 0

можно преобразовать с подстановкой выражений для погонных ёмкости и индуктивности.

Известно (будет показано в последующих лекциях при рассмотрении разделов расчета поля в плоскопараллельных линиях), что для длинных линий с плоскопараллельной структурой электромагнитного поля (напомним, что так называют поля, которые имеют одинаковые выражения в каждом поперечном сечении длинной линии, чему соответствуют все типы двусвязных линий) справедливо равенство

1	=	1	1	,
L 0 C 0	=	ε 0 µ 0	ε r µ r	,

где ε 0 , µ 0 , ε , µ − диэлектрическая и магнитная проницаемости вакуума и относительные проницаемости среды конструктивного исполнения длинной ли-

нии; c =	1	− скорость света в вакууме.
	ε 0 µ 0
Тогда фазовая скорость v =			1	1	=	c	, т.е. в воздушной линии,
Тогда фазовая скорость v =			ε 0 µ 0	ε r µ r	=	ε r µ r	, т.е. в воздушной линии,
у которой ε=1,		µ=1 фазовая скорость волны совпадает со скоростью света, в

коаксиальном кабеле с диэлектрическим заполнением v < c.

Аргумент волнового сопротивления линии без потерь θ = 0, т.е. токи прямой и обратной волн совпадают по фазе с напряжениями.

Уравнения длинной линии с гиперболическими функциями от комплексного аргумента при заданных напряжении и токе в конце линии (на нагрузке) при отсчете продольной координаты х от нагрузки записаны в виде:

U ( x ) =U 2 chγx + Z B I 2 sh γx ,

I ( x ) =	U 2	sh γx + I 2	chγx .	(6.8)
	Z B

Для линии без потерь γ = jβ и формулы (6.8)				с учетом равенств

ch γx = ch jβx = cosβx и sh γx =sh jβx = j sinβx

преобразуются к виду

U ( x ) =U 2 cosβx + jZ B I 2 sinβx ,

Входное сопротивление отрезка линии или в любом сечении линии при отсчете длины х от нагрузки имеет вид:

U (x)

2 cosβx + jZB I 2 sinβx

= Z

ВХ

I (x)

U 2

sinβx + I 2 cosβx

= Z B Z H + Z B tgβx .

Z B + Z H tgβx

		U		2
		U

					+
cosβx		I 2			+		jZB tgβx
		I 2						=
			U		2			=

	j

cosβx			I 2			tgβx + ZB
			I 2

(6.10)

Переходя в уравнениях (6.9) к мгновенным значениям при U 2					=U 2 и I 2 =
= I 2 e jϕ2 , получаем
	ωt +	π	−ϕ2		(6.11)
u =U 2m cosβx sin ωt + I 2m zВ sinβx sin	ωt +	2	−ϕ2	;	(6.11)
		2

i =	U2m		ωt +	π	+ I2m cosβxsin(ωt − ϕ2 ).	(6.12)
	zВ	sinβxsin
				2

Кривые распределения мгновенных значений тока и напряжения вдоль длинной линии на расстоянии, равном длине волны, при ϕ2 > 0для трех момен-

тов времени представлены на рис. 6.2. Кривые на рис. 6.2 и формулы (6.11) и (6.12) показывают, что распределение напряжения и тока вдоль линии в каждый момент является синусоидальным. Рассматривая их одновременно, видим, как изменяются кривые распределения тока и напряжения по линии на протяжении

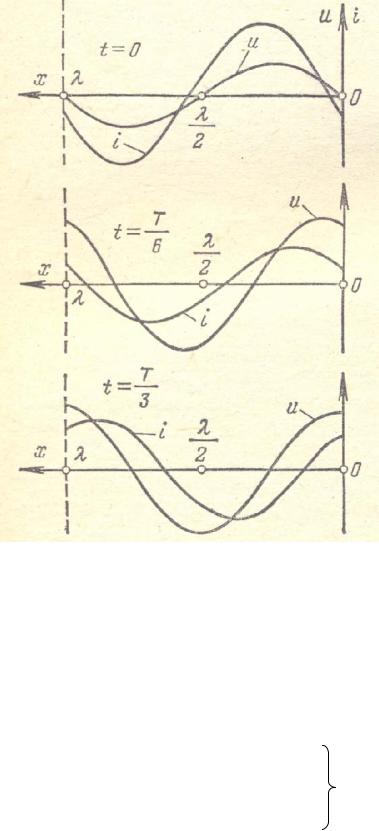
трети периода. Изменение тока или напряжения во времени в любой фиксированной точке линии также будет синусоидальным.

Рисунок 6.2 – Распределение мгновенных значений тока и напряжения вдоль линии для трех моментов времени

Остановимся ещё на свойствах линий без потерь, длиной в четверть и в по-

ловину длины волны. При линии длиной l =

λ получим βl =

2π

, из чего в

соответствии с (6.8):

1 =

2 cos

π +

jZB I 2 sin π

= jZB I 2 ,

I1 = j

U 2

sin π + I 2 cos π = j

U 2

sin

π .

(6.13)

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете Теория передачи информации

#
13.03.2016407.72 Кб29Методы и средства передачи информации (Лекция №18).pdf
#
13.03.2016451.67 Кб32Методы и средства передачи информации (Лекция №2).pdf
#
13.03.2016367.22 Кб40Методы и средства передачи информации (Лекция №3).pdf
#
13.03.2016539.34 Кб24Методы и средства передачи информации (Лекция №4).pdf
#
13.03.2016662.05 Кб30Методы и средства передачи информации (Лекция №5).pdf
#
13.03.2016578.22 Кб27Методы и средства передачи информации (Лекция №6).pdf
#
13.03.2016782.16 Кб34Методы и средства передачи информации (Лекция №7).pdf
#
13.03.2016324 Кб21Методы и средства передачи информации (Лекция №8).pdf
#
13.03.2016579.29 Кб37Методы и средства передачи информации (Лекция №9).pdf