
Методы и средства передачи информации (Лекция №3)
.pdf
Методы и средства передачи
 информации
информации
Лекционный курс
Лекция №3
Содержание
1.Введение в теорию длинных линий. Понятие «длинная линия».
2.Эквивалентная схема однородной длинной линии и метод расчета режима в линии.
3.Уравнения длинной линии с гиперболическими функциями.
4.Характеристики однородной линии.
5.Входное сопротивление длинной линии.
6.Коэффициент отражения волны.
7.Согласованная нагрузка линии.
1.Введение в теорию длинных линий.
Понятие «длинная линия»
Понятие «длинная линия» применяется для идентификации электрических цепей, продольные размеры которых соизмеримы с длиной волны λ (как правило, от 0,1λ и больше), в результате чего проявляется эффект запаздывания (т.е. присутствует и учитывается интервал времени) при передаче сигнала (прохождении электромагнитной волны) вдоль линии передачи. При этом важно, что в поперечном направлении линии передачи геометрические размеры много меньше длины волны, т.е. в поперечном направлении предполагаются справедливыми соотношения для цепей с сосредоточенными параметрами. Эти соотношения сводятся к выполнению свойства «дальнодействия», которое проявляется в отсутствии временных сдвигов между воздействием на цепь и возникающей при этом реакции (другими словами, действие источника мгновенно проявляется на удаленных объектах). В противовес этому в длинных линиях проявляется эффект «близкодействия», когда реакции подвержены участки цепи, находящиеся в непосредственной близости к источнику возмущения. При этом само возмущение перемещается последовательно между соседними участками цепи, а этому соответствует задержка в проявлении реакции на подключенное к цепи внешнее воздействие.
Пассивные цепи с сосредоточенными параметрами описываются эквивалентными схемами, которые могут содержать сосредоточенные элементы: резисторы, емкости и индуктивности. Понятие «сосредоточенный» элемент эквивалентной электрической схемы указывает на справедливость допущения для описания процессов в нём приближения дальнодействия, т.е. указывает, что значения токов в элементе (во всех его частях) одинаковы для одного и того же момента времени. Заметим, что только для сосредоточенных элементов справедливы ком-
понентные уравнения (уравнения по закону Ома): u = r i ; u = L |
∂ i |
; |
u = |
1 |
∫i dt , |
|
|||||
∂t |
C |
где r, L, C − соответственно, значения сопротивления резистора, индуктивности и емкости в эквивалентной схеме замещения элементов цепи.
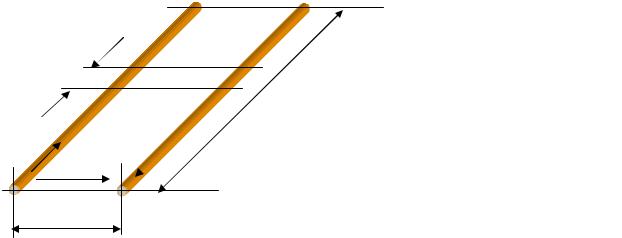
Конструктивно, в простейшем случае длинную линию можно представить в виде параллельно размещенных проводников двухпроводной линии (рис. 3.1).
|
∆x |
|
|
l |
Рис. 3.1 − Простейший вид двухпро- |
i |
водной линии связи. l ≥ λ; a << λ |
|
i |
|
|
|
|
|
|
u |
|
а
Чтобы описать процесс изменения электрического тока и напряжения вдоль линии, нужно считать, что сколь угодно малый по длине ∆ x элемент линии обладает сосредоточенными сопротивлением и индуктивностью, а между проводами − проводимостью и емкостью, т.е. рассматривать линию как цепь с распределенными сосредоточенными параметрами. При этом предполагаем, что продольные сопротивление и индуктивность и поперечные проводимость и емкость равномерно распределены вдоль линии, и образуют погонные продольные сопротивление и индуктивность и поперечные проводимость и емкость, которые называют пер-
2

вичными параметрами длинной линии. Это является определенной идеализацией реальной линии, на погонные параметры которой оказывает влияние окружающая среда, предметы и конструктивное положение проводников. При постоянстве первичных параметров линии вдоль её длины длинная линия называется однородной.
2. Эквивалентная схема однородной длинной линии
иметод расчета режима в линии
Встационарном режиме вдоль длинной линии, подключенной к источнику сигнала, устанавливается определенная картина распределения действующих значений напряжения и тока, причем в каждом сечении линии возникает своя картина мгновенных значений токов и напряжений. Расчет режима в длинной линии предполагает определение мгновенных и действующих значений напряжения и токов вдоль длинной линии. Алгоритм расчета режима в длинной линии основан на применении уравнений состояния (уравнений Кирхгофа) к расчету эквивалентной схемы модели длинной линии.
Эквивалентная схема модели линии возникает из представления однородной длинной линии в виде каскадного соединения бесконечного множества одинаковых Г-образных четырехполюсников, соответствующих отрезкам ∆х линии, которые много меньше длины волны (рис. 3.2). В схеме, четырехполюсники образованы сосредоточенными элементами из первичных параметров однородной ли-
|
|
|
|
|
i + |
∂i |
|
|
|
r0 dx |
L0dx |
i |
r0 dx |
L0dx |
∂x dxr0 dx |
|
L0dx |
||
Г-образный |
|
a |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
четырехполюсник |
u g0 dx |
|
C0dx |
g0 dx |
|
C0dx |
u |
+ |
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
c |
|
|
c |
|
|
|
|
∆x→dx |
x |
|
|
|
|
Рис. 3.2 − Схематичная модель для участка dx лини передачи |
3 |
|
|
|
|
нии, отнесенных к единице её длины: r0 − сопротивления прямого и обратного провода; L0 − индуктивности, которую можно интерпретировать индуктивностью петли, образованной прямым и обратным проводами, причем с учетом влияния окружающих условий, как правило, подложки плат полосковых линий, или земли в воздушных линиях − это рабочая индуктивность петли; g0 − проводимость (утечки тока) между проводами длинной линии; С0 − ёмкость между проводами (или с учетом ёмкости проводов по отношению к земле или окружающим предметам − рабочая ёмкость между проводами). При этом каждый участок ∆х ≈ dx ли-
нии |
линию содержит продольное сопротивление r0 dx и продольную индуктив- |
ность |
L0 dx (которые относятся и к верхнему на рис. 3.2 (называют − «прямому») |
и к «обратному» (на рис. 3.2 − нижнему) проводам, а потому должны быть включены в провода эквивалентной схемы в половинном значении, но для удобства будем считать их включенными в один провод, учитывая, что при последовательном соединении сопротивления суммируются, а, как мы увидим, эти элементы в уравнения состояния входят в виде последовательного соединения), поперечные g0 dx − проводимость и С0 dx − ёмкость.
Составим дифференциальные уравнения, которым удовлетворяют токи и напряжения в любом сечении двухпроводной линии. Обозначим через х расстояние от начала линии до некоторого текущего элемента её длины (иными словами − некоторого поперечного сечения). Мгновенные значения напряжения и тока в начале выбранного элемента dx обозначим через u и i, а в конце этого элемента,
т.е. в начале следующего элемента dx − через u + |
∂u |
dx |
и i + |
∂i |
dx . Положитель- |
|
∂x |
|
∂x |
||
ные направления токов и напряжений соответствуют указанным на рис. 3.2.
Для элемента линии длиной dx уравнения по законам Кирхгофа запишем в
виде:
− по второму закону Кирхгофа для контура a−b−c
|
∂u |
|
= (r0 dx )i +(L 0 dx ) |
∂i |
; |
|
u − u + |
|
dx |
|
|||
∂x |
∂t |
|||||
|
|
|
|
− по первому закону Кирхгофа для узла b
4
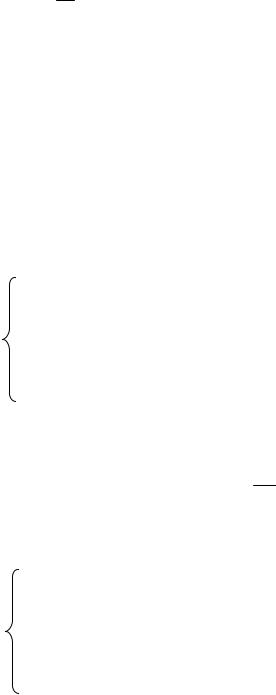
i − i + ∂i dx∂x
Заметим,
|
|
|
|
∂u |
|
|
|
|
∂ |
∂u |
|
|
|
= ( g |
0 |
dx ) u + |
|
dx |
+(C |
0 |
dx ) |
|
u + |
|
dx . |
|
|
|
||||||||||
|
|
|
∂x |
|
|
|
|
|
∂x |
|
||
|
|
|
|
|
|
|
|
∂t |
|
|||
последние слагаемые в уравнениях представляют собой компо-
нентные уравнения для напряжения на индуктивности u L |
= L |
∂i |
и тока в ёмко- |
||
|
|||||
|
|
|
|
∂t |
|
сти u C = |
1 |
∫i dt . |
|
|
|
C |
|
|
|
||
Раскрывая скобки, приводя подобные члены и сокращая на dx, получаем систему дифференциальных уравнений:
− |
∂u |
= r0 i + L 0 |
∂i |
; |
|
||
∂x |
|
|
|||||
|
|
∂t |
|||||
− |
∂i |
|
= g 0 u + g 0 |
|
∂u |
dx +C 0 |
|
∂x |
|
||||||
|
|
|
∂x |
||||
∂u |
|
|
∂ ∂u |
|
||
|
+C |
0 |
|
|
|
dx . |
|
|
|
||||
∂t |
|
|
|
∂x |
|
|
|
|
∂t |
|
|||
Пренебрегая величинами второго порядка малости, т.е. предполагая:
∂u u >> ∂x dx
получим систему в виде:
− |
∂u |
= r0 i + L 0 |
∂i |
; |
|
(3.1) |
||
∂x |
|
|
||||||
|
|
∂t |
|
|||||
− |
∂i |
|
= g 0 u +C 0 |
|
∂u |
. |
(3.2) |
|
∂x |
|
|||||||
|
|
|
∂t |
|
||||
Решение полученной системы дифференциальных уравнений в частных производных при определенных начальных и граничных условиях дает возможность определить ток и напряжение как функции расстояния от начала линии и времени. Эти уравнения справедливы при любых изменениях во времени источников тока и напряжения, подключенных к линии.
Начнем рассмотрение методов расчета с установившегося режима в однородной длинной линии.
5

Рассмотрим установившийся режим в длинной линии при синусоидальном напряжении источника питания. В этом случае рационально осуществить переход в частотную область, вводя комплексные напряжения и токи (см. с. 9 и с. 10 лекции №1), комплексные сопротивления и проводимости. Напомним, что последние возникают как следствие применения компонентных уравнений к изображению тока и напряжения на комплексной плоскости в результате действий:
1) из u L = L ∂∂ti с учетом представления синусоидальной функции
|
|
|
f ( t ) =Fm sin (ω t + φf ) → F m e |
j ωt |
e |
j ϕ f |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
U m L e j ωt e j ϕ u |
= L |
∂ |
(I m L e j ( ωt+ϕ i ) ) |
= LI m |
L jωe j ( ωt+ϕ i ) = jωL I m L e jωt e jϕ i |
|||||||||||||
∂t |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или, проводя сокращение на e j ωt , получим |
U m L |
e j ϕ u |
= jωL I m L |
e jϕ i ; |
||||||||||||||
2) из u = |
1 |
∫i dt аналогично получаем |
|
|
|
|
|
|
|
|
|
|
||||||
C |
|
|
|
|
|
|
|
|
|
|
||||||||
U m C e j ωt e j ϕ u |
= |
1 |
|
I m L e j ( ωt+ϕ i ) d t |
= |
1 |
I m L e jωt e jϕ i |
|
|
|
||||||||
C ∫ |
jωC |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или, проводя сокращение на e j ωt , получим |
U m L |
e j ϕ u |
= |
1 |
I m L |
e jϕ i . |
||||||||||||
jωC |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, переписывая уравнения (3.1) и (3.2) с учетом комплексных напряжения и тока, сопротивления и проводимости, получаем:
− |
∂ |
U |
|
= (r0 |
+ jωL 0 |
)I = Z 0 |
I ; |
(3.3) |
||||||
|
|
|||||||||||||
∂x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
− |
|
∂I |
|
= ( g 0 |
+ jωC 0 |
) |
U |
=Y 0 |
|
U |
, |
(3.4) |
||
|
∂x |
|||||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
где Z 0 = (r0 + jωL 0 ) − продольное (удельное) комплексное сопротивление длинной линии,
Y 0 = ( g 0 + jωC 0 ) − поперечная (удельная) комплексная проводимость
длинной линии, причем Z 0 ≠ |
1 |
, так как это чисто формальные обозначения. |
|
Y 0 |
|||
|
|
6
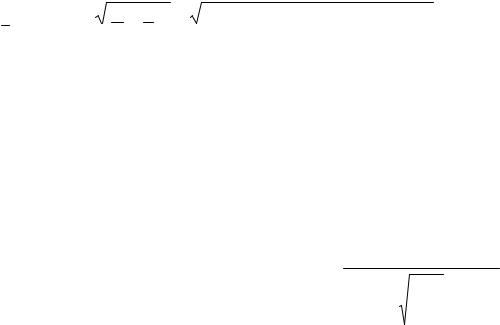
Для перехода от системы дифференциальных уравнений относительно комплексных напряжения U и тока I к уравнениям относительно одной из функций (напряжения или тока) продифференцируем уравнения (3.3) и (3.4):
|
− |
∂ 2 |
U |
|
|
|
= Z 0 |
|
∂ I |
; |
|
|
− |
∂ 2 I |
=Y 0 |
∂ |
U |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
∂x |
|||||||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
∂ x |
|
|
|
|
∂x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и заменим |
|
∂ I |
и |
|
|
|
∂ |
U |
|
|
согласно (3.4) и (3.3). Тогда получим: |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
∂ x |
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
∂ 2 U |
|
= Z 0 |
Y 0 |
|
U |
; |
|
|
(3.5) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
∂x 2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
∂ 2 I |
|
= Z 0 |
Y 0 |
I . |
|
|
|
(3.6) |
|||||||||||||||
|
|
|
|
|
|
∂x 2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Полученные дифференциальные уравнения (3.5) и (3.6) определяют изменение комплексных напряжения и тока вдоль длинной линии. Они одинаковы. Поэтому, достаточно, например, получить из уравнения (3.5) закон изменения напряжения U (х), а ток I (х) получить из уравнения (3.3).
Решение уравнения (3.5) − линейного дифференциального уравнения второго порядка с постоянными коэффициентами − имеет вид:
U = A 1 e − γx + A 2 e γx |
= A 1 e −α x e − j β x + A 2 e α x e j β x , |
(3.7) |
где γ = α+ jβ = Z 0 Y 0 = (r0 |
+ j ωL 0 )( g 0 + j ωC 0 ); |
(3.8) |
А 1, А 2 − комплексные постоянные интегрирования, которые находят из граничных условий на концах линии.
Заметим, что справедливость записанного решения для U (х) легко проверить его подстановкой в уравнение (3.5).
Прежде чем искать постоянные интегрирования, получим выражение для тока, применив уравнение (3.3):
|
1 ∂ |
U |
|
γ |
|
−γx |
γx |
(A 1 e − γx − A 2 |
e |
γx ) |
|
|
|||||
|
|
|
|
|
|
|
|
(A 1 e |
|
− A 2 e )= |
|
|
|
|
|
. |
(3.9) |
I = − Z 0 ∂x = Z 0 |
|
|
Z 0 |
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Y 0 |
|
|
|
|
|
7
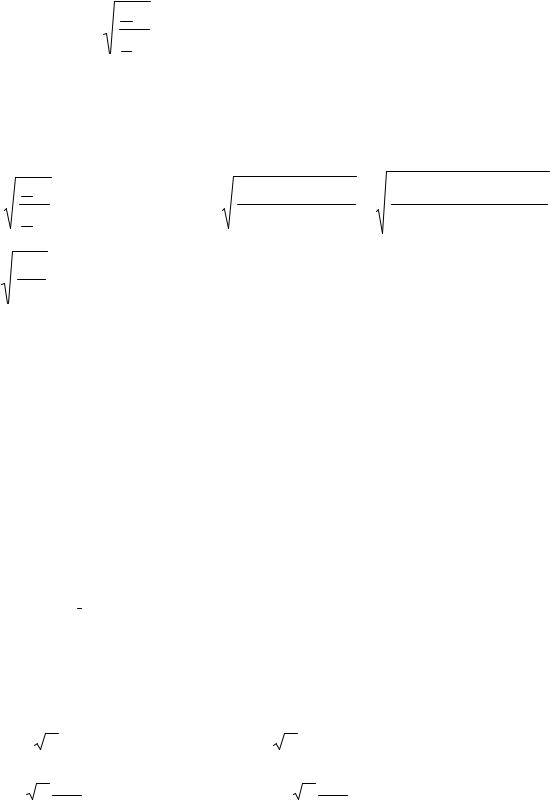
Выражение |
Z 0 |
в знаменателе формулы (3.9) имеет размерность сопро- |
|
Y 0 |
|||
|
|
тивления − Ом и его называют (чисто формально) волновым сопротивлением линии, обозначая идентификатором Z В. Волновое сопротивление связано с первич-
ными параметрами линии соотношениями:
Z В= |
Z |
0 |
|
= Z e |
j θ |
= rB + |
jx B = |
(r0 + |
j ωL 0 ) |
= 4 |
(r0 )2 + (ωL 0 |
)2 |
j θ |
= |
||||||||||||||
Y |
|
|
|
( g 0 |
+ |
j ωC 0 ) |
( g 0 )2 + (ωC 0 |
e |
|
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
)2 |
|
|
|||||||||||||||
= |
Z |
0 |
|
e |
j θ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
|||
Y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где θ = |
1 |
[arg (r0 + j ωL |
0 )− arg ( g 0 |
+ |
j ωC 0 )]= arctg |
ωL 0 |
− arctg |
ωC 0 |
= |
|
||||||||||||||||||
2 |
|
r0 |
g 0 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ω( g 0 L 0 − r0 C 0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
=arctg |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.11) |
|||
r0 g 0 + ω2 L 0 C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Для однородной линии, рассматриваемой как четырехполюсник волновое |
|||||||||||||||||||||||||||
сопротивление совпадает с характеристическим сопротивлением Z C − также чис- |
||||||||||||||||||||||||||||
то формальным образованием. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Подставляя (3.10) в формулу (3.9) запишем её в виде |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
I = |
1 |
(A 1 e −γx |
− A 2 e γx |
|
)= |
|
A 1 |
|
e −αx e − jβx |
+ |
A 2 |
|
e αx e jβx . |
(3.12) |
|||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Z B |
|
Z B |
|
Z B |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Выражая комплексы A 1 и A 2 в виде A 1 = A1 e jΨ1 |
и A 2 |
= A2 e jΨ2 |
, запи- |
||||||||||||||||||||||||
шем мгновенные значения напряжения и тока: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
u ( x , t ) = |
|
2A1 e −αx sin (ωt −βx +Ψ1 |
)+ |
2A2 e αx sin (ωt +βx +Ψ2 |
); |
(3.13) |
||||||||||||||||||||||
i ( x , t ) = |
2 |
A1 e −αx sin (ωt −βx +Ψ1 |
−θ)+ |
|
2 A2 e αx |
sin (ωt +βx +Ψ2 −θ). (3.14) |
||||||||||||||||||||||
|
|
|
|
|
Z B |
|
|
|
|
|
|
|
|
|
|
Z B |
|
|
|
|
|
|
|
|
|
|
|
|
Каждое из слагаемых в правой части в формулах (3.13) и (3.14) можно рассматривать как электромагнитную волну, распространяющуюся (поэтому их называют «бегущие волны») в направлении возрастания или убывания координаты х. Из физических соображений ясно, что распространение волны должно сопро-
8
вождаться убыванием её амплитуды (говорят, затухания волны), которое в формулах определено экспоненциальным коэффициентом. Учитывая положительное значение сомножителя α в показателе степени экспоненты, ясно, что первые слагаемые в обеих формулах соответствуют волне распространяющейся в направлении оси х (её называют прямой волной), а вторые слагаемые − описывают волну распространяющуюся (бегущую) в обратном направлении (её называют обратной волной).
Итак, каждое из слагаемых в формулах (3.13) и (3.14) в любой фиксированной точке х = х1 представляет собой периодическую функцию времени. В любой же фиксированный момент времени t = t1 каждое из слагаемых изменяется вдоль линии (вдоль оси х) по закону затухающей синусоиды.
В соответствии со свойствами величин γ =α + jβ, α и β в формулах (3.13) и
(3.14), их называют: γ − постоянная (или коэффициент) распространения, α −
коэффициент затухания и β − коэффициент фазы. Это величины, приведенные к единице длины линии. Их называют вторичные параметры линий в отличии от её первичных параметров (погонных сопротивления, проводимости, индуктивности и ёмкости).
Основными характеристиками бегущей волны являются фазовая скорость и длина волны (надо заметить, что это − величины приведенные к единице длины).
Фазовая скорость волны v − скорость перемещения какой либо определенной фазы (состояния возмущения, или определенного мгновенного значения напряжения или тока) колебания, которая в течение времени t и по мере увеличения расстояния х, пройденного волной, остается постоянной, т.е. для прямой волны
ωt −βx + Ψ1 = const , а для обратной волны |
ωt +βx + Ψ2 |
= const . |
|
||||||||||
Тогда для прямой волны |
|
∂ |
(ωt −βx + Ψ1 )= 0 , т.е. |
|
∂x |
= |
ω |
= v. |
(3.15) |
||||
|
|
|
|
|
|
||||||||
|
∂t |
|
∂t |
β |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
Для обратной волны |
∂ |
(ωt +βx + Ψ2 |
)= 0 , т.е. |
∂x |
|
= − |
ω |
= −v. |
(3.16) |
||||
|
|
|
|
||||||||||
∂t |
∂t |
|
β |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
9
Отрицательный знак скорости распространения волны указывает на противоположное направление её распространения. Таким образом, это еще одно подтверждение представления слагаемых в (3.13) и (3.14) в виде волн, движущихся в противоположных направлениях.
Длиной волны λ называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания в которых совпадают (т.е. различаются на 2π, так как фаза с изменением х нарастает). Следовательно, для первого слагаемого равенства (3.13) получим:
ωt −βx + Ψ1 = ωt −β( x + λ )+ Ψ1 + 2 π, или 0 = −βλ+ 2 π,
откуда |
|
|
λ = |
|
2 π |
. |
|
|
(3.17) |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
β |
|
|
|
|
|
||
С учетом (3.17) |
v = |
ω |
= |
2 |
πf |
= λf |
= |
λ |
, т.е. за время равное периоду колебаний |
||||
|
|
|
|
|
T |
||||||||
β |
β |
||||||||||||
|
|
|
|
|
|
|
|||||||
волна (точнее сказать фиксированное значение фазы, т.е. состояния процесса) пробегает расстояние равное длине волны.
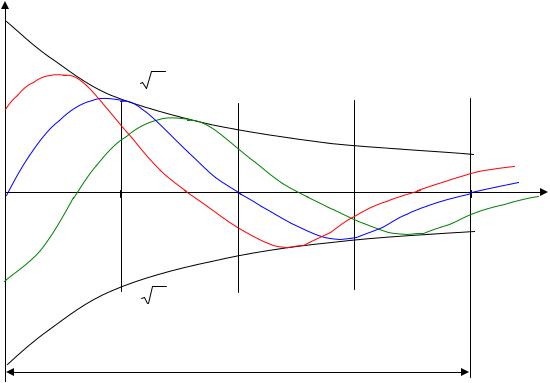
Затухающая вдоль оси х синусоидальная волна представлена на рис. 3.3. На
u |
|
t1< t2< t3 |
|
|
|
|
|
|
|
|
t1 |
+ |
2A1 e |
−α x |
|
|
|
t2
t3
х
−2A1 e −α x
λ
Рис. 3.3 − Зависимость волны напряжения от сечения длинной линии для трех моментов времени
10
