2639 Высшая математика. Лаврусь, Лаврусь

2639	Министерство транспорта Российской Федерации
	Федеральное агентство железнодорожного транспорта
	ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
	САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра «ВЫСШАЯ МАТЕМАТИКА»

ВЫСШАЯ МАТЕМАТИКА

Методические указания и варианты заданий к экзаменационному тесту (ряды, теория вероятностей, математическая статистика)

для студентов заочной формы обучения

Составители: О.Е. Лаврусь В.В. Лаврусь

Самара

2010

УДК 519.7

Высшая математика : методические указания и варианты заданий к экзаменационному тесту (ряды, теория вероятностей, математическая статистика) для студентов заочной формы обучения / составители : О.Е. Лаврусь, В.В. Лаврусь. – Самара :

СамГУПС, 2010. – 62 с.

Утверждены на заседании кафедры 15.09.2010 г., протокол № 2. Печатаются по решению редакционно-издательского совета

университета.

Тестовые работы предназначены для проверки уровня теоретических знаний и практических навыков, полученных студентами в течение семестра, и могут быть использованы для принятия зачета, экзамена, а также для проверки остаточных знаний.

Составители: к.т.н., доцент О.Е. Лаврусь к.т.н. В.В. Лаврусь

Рецензенты: к.ф.м.н., доцент СамГУПС Л.В. Кайдалова; к.ф.м.н., доцент СамГУ Г.В. Воскресенская

Под редакцией составителей

Подписано в печать 04.10.2010. Формат 60×90 1/8. Усл. печ. л. 7,75. Заказ № 227.

© Самарский государственный университет путей сообщения, 2010

МЕТОДИЧЕСКИЕ УКАЗАНИЯ к тестовой работе

Сборник включает 30 вариантов тестовой работы по таким разделам высшей математики, как ряды, теория вероятностей и математическая статистика.

Каждый вариант состоит из 21 вопроса. На каждый вопрос предлагается 4 варианта ответа, из которых правильным является только один. Тестируемый студент выбирает тот вариант ответа, который ему представляется верным. Выбранный вариант ответа заносится студентом в контрольный лист теста.

Преподаватель проверяет правильность ответов с помощью таблицы-ключа, содержащей правильные ответы для каждого

варианта.
На выполнение тестовой работы отводится 45 минут.
Предлагается	следующая	система	оценки	знаний:
за 18–21 правильных ответов –		отлично, за	14–17 –	хорошо,

за 8–13 – удовлетворительно, за число правильных ответов менее 7 – неудовлетворительно.

Приложения:

1.Тестовые задания (30 вариантов).

2.Контрольный лист теста.

3.Проверочная таблица-ключ.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика)	Составитель: Лаврусь О.Е.
ВАРИАНТ 1	Лаврусь В.В.

1. Для знакоположительного числового ряда

A)радикальным признаком Коши;

B)признаком Даламбера;

C)признаком Лейбница;

D)признаком сравнения.

∞

3

n

2. Третий член ряда ∑

равен:

2

A) 0,75;

n=1

(2n −1)

B) 0,9;

C) 1,5;

D) 1,08.

3. n-й член ряда

1

+

1

+

1

+ 1

… равен:

2

3

4

5

∞

1

A) ∑

;

n=1

n

∞

1

B) ∑

;

n +

1

n=1

∞

1

C) ∑

;

n +

1

n=0

∞

1

D) ∑

.

n + 2

n=1

4. Сумма первых трех членов ряда ∑∞ (−1)n n=1 3n − 1

	A)	33	;	B) –	17	;	C)	17	;
		40			40			40

	∞				an+1
	∑	a	n	предел lim		= p называется:
					an
				n→∞
	n=1

равна:

D) – 3340 .

∞	n
5. Найти интервал сходимости функционального ряда ∑	(x − 1)	:
	n+1
n=1	2
A) – 2 < x < 2;
B) – 1 < x < 3;
C) – 3 < x < 1;
D) 0 < x < 1.

6. Пусть известна вероятность Р(А) события А. Тогда вероятность противоположного события А определяется по формуле:

A) Р(А)= Р(А)−1 ;

B) Р(А)= 1− Р(А);

	C) Р(			)=		1		;
		А
						Р(А)
	D) Р(				)= 0,5 Р(А).
			А
	7. Комбинации, число которых определяется по формуле Cnm =								n!		, называются:
									m!(n − m)!

A) сочетаниями;

B) размещениями;

C) перестановками;

D) размещениями с повторением.

8.Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,8, для второго – 0,9. Найти вероятность того, что в мишень попадет только один стрелок.

A) 0,02; B) 0,72; C) 0,98; D) 0,26.

9.Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет ровно 3 раза.

A)3/5;

B)5/16;

C)5/32;

D)3/16.

10. Вероятность наступления события A в каждом испытании равна 0,4. Вероятность того, что в результате проведения 100 независимых испытаний событие A наступит ровно 16 раз, вычисляется:

A)по локальной формуле Муавра-Лапласа;

B)по интегральной формуле Лапласа;

C)по формуле Бернулли;

D)по формуле Пуассона..

11. Плотностью вероятности f(x) непрерывной случайной величины X называется:

A)производная функции распределения случайной величины X;

B)первообразная функции распределения случайной величины X;

C)производная случайной величины X;

D)первообразная случайной величины X.

12. Дискретная случайная величина X задана законом распределения:

xi	0	x2	9
pi	0,1	0,5	0,4

Если известно, что ее математическое ожидание M(X) равно 5,6, то x2 равно:

A)3;

B)4;

C)5;

D)6.

ВАРИАНТ 1

13.Найти дисперсию случайной величины Z = 2X – 3Y + 1, если известны дисперсии независимых случайных величин X и Y: D(X) = 2, D(Y) = 2.

A) – 1; B) 26; C) 27; D) 10.

14.Случайная величина X задана интегральной функцией:

0 при x ≤ 0;

F(x)= x2 при 0 < x ≤ 4;

16

1 при x > 4.

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (1, 3).

A)7/16;

B)5/16;

C)1/16;

D)1/2.

15. Дана дифференциальная функция случайной величины X:

	0		при x ≤ −1;
	1
	f (x)=		при − 1 < x ≤ 2;
		3
			при x > 2.
	0

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (– 1, 0).

A)2/3;

B)1/3;

C)3/4;

D)1/2.

16. Случайная величина X задана интегральной функцией:

0				при x ≤ −1;
x + 1
F(x)=				при − 1 < x ≤ 3;
		γ
				при x > 3.
1

Коэффициент γ равен:

A)2;

B)3;

C)4;

D)1.

17. Найти моду статистической выборки: 1, 4, 5, 1, 3, 4, 2, 1, 3, 2, 5.

A)4;

B)5;

C)2;

D)1.

18. Если основная гипотеза имеет вид H0: a = 9, то конкурирующей может быть гипотеза:

A)Н1: a ≠ 8;

B)Н1: a < 9;

C)Н1: a ≤ 9 ;

D)Н1: a ≥ 9.

19. Точечная оценка математического ожидания случайной величины, распределенной по нормальному закону, равна 10. Тогда его интервальная оценка может быть записана в виде:

A)(8,5; 11,5);

B)(8,6; 10,6);

C)(8,4; 10,2);

D)(10; 10,9).

20. Из генеральной совокупности извлечена выборка объема n = 70, полигон относительных частот которой имеет вид

wi

0,5

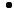
0,1

0

2

4

6

8 xi .

Тогда число вариант x2 = 4 в выборке равно:

A)28;

B)14;

C)35;

D)8;

21. Выборочное уравнение парной регрессии имеет вид y = 8 – 2x. Тогда выборочный коэффициент корреляции может быть равен:

A)4;

B)– 2;

C)0;

D)– 0,8.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика)

Составитель: Лаврусь О.Е.

ВАРИАНТ 2

Лаврусь В.В.

1. Пусть

∞

a

– знакоположительный числовой ряд. Тогда lima

= 0 есть:

7. Комбинации, число которых определяется по формуле Anm =

n!

, называются:

n=1

(n

− m)!

n→∞

n

∑ n

A) признак сравнения;

A) размещениями без повторений;

B) необходимый признак сходимости;

B) перестановками;

C) достаточный признак сходимости;

C) размещениями с повторениями;

D) признак Даламбера.

D) сочетаниями.

2. Третий член ряда

∞

(−1)n+1 3n

равен:

8. Брошены две

игральные кости. Найти вероятность того,

что

сумма очков на

∑n=1 (2n −1)2

выпавших гранях равна 3.

A) 0,75;

A) 1/6;

B) – 1,08;

B) 1/9;

C) 1,5;

C) 1/18;

D) 1,08.

1

1

1

D) 1/12.

3. n-й член ряда 1 −

+

−

… равен:

4

2

3

9. Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при

∞

1

A) ∑(− 1)n

;

каждом выстреле одинакова и равна 0,8. Найти вероятность того, что стрелок попадет в

n=1

n

мишень ровно 2 раза.

∞

(− 1)n+1

1

A) 0,512;

B) ∑

;

n

B) 0,384;

n=1

∞

(− 1)n

1

C) 0,64;

C) ∑

;

D) 0,096.

n

n=0

∞

1

D) ∑(− 1)n

.

10. Вероятность наступления события A в каждом испытании равна 0,001. Вероятность

n=2

n

того, что в результате проведения 1000 независимых испытаний событие A наступит

∞

n+1

ровно 5 раз, вычисляется:

4. Сумма первых трех членов ряда ∑

(− 1)

равна:

A) по формуле Пуассона;

2n − 1

B) по интегральной формуле Лапласа;

n=1

A) –

8

;

B) –

10

;

C)

13

;

D) –

7

.

C) по формуле Бернулли;

D) по локальной формуле Муавра-Лапласа.

15

15

15

15

∞

n

5. Найти интервал сходимости функционального ряда ∑

(x − 2)

:

11. Среднее квадратическое отклонение σ(X) случайной величины X находится по

n+1

n=1

3

формуле:

A) – 2 < x < 2;

A) σ (X )= M (X ) ;

B) – 3 < x < 3;

B) σ (X )=

1

C) – 1 < x < 5;

;

D) – 5 < x < 1.

D(X )

6. Вероятность Р(А) появления достоверного события А определяется из условия:

C); σ (X )=

D(X ) ;

A) 0 ≤ Р(А) ≤ 1;

D) σ (X )=

1

B) Р(А) ≤ 1;

.

M (X )

C) Р(А) > 0;

D) Р(А) = 1.

ВАРИАНТ 2

12. Дискретная случайная величина X задана законом распределения:

xi	– 1	0	5
pi	0,4	0,2	p3

Математическое ожидание M(X) этой случайной величины равно:

A)4;

B)2,4;

C)1,6;

D)1,8.

13. Найти дисперсию случайной величины Z = 3X – 2Y, если известны дисперсии независимых случайных величин X и Y: D(X) = 6, D(Y) = 1.

A)16;

B)50;

C)58;

D)20.

14. Случайная величина X задана интегральной функцией:

		0		при x ≤ −3;
			x
	F(x) =	1+		при − 3 < x ≤ 0;
			3
				при x > 0.
		1

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (– 3, – 1).

A)1/3;

B)2/3;

C)1/2;

D)3/4.

15. Дана дифференциальная функция случайной величины X:

0 при x ≤ 0;

f (x) = 2x при 0 < x ≤ 3;9

0 при x > 3.

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (0, 1).

A)1/3;

B)5/9;

C)1/9;

16. Дана дифференциальная функция случайной величины X:

0 при x ≤ 0;

f (x) = 3x2 при 0 < x ≤ 1;0 при x > 1.

Математическое ожидание X равно:

A)1/4;

B)1/2;

C)3/4;

D)5/8.

17. Найти моду статистической выборки: 1, 2, 3, 3, 2, 4, 5, 3, 4, 1.

A)2;

B)5;

C)3;

D)4.

18.. Если основная гипотеза имеет вид H0: a = 20, то конкурирующей может быть гипотеза:

A)Н1: a ≥ 10;

B)Н1: a ≥ 20;

C)Н1: a ≤ 20;

D)Н1: a ≠ 20.

19.Точечная оценка математического ожидания случайной величины, распределенной по нормальному закону, равна 11. Тогда его интервальная оценка может быть записана в виде:

A) (11; 11,5); B) (10,5; 11,6); C) (10,6; 11,5); D) (10,5; 11,5).

20.Из генеральной совокупности извлечена выборка объема n = 40 , полигон относительных частот которой имеет вид

wi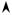

0,4 0,3

0,1

0

1

2

3

4 xi .

Тогда число вариант x1 = 1 в выборке равно:

A)10;

B)8;

C)12;

D)20;

21. Выборочное уравнение парной регрессии имеет вид y = 3x + 2. Тогда выборочный коэффициент корреляции может быть равен:

A)0,6;

B)3;

C)0;

D)– 0,8.

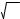
Экзаменационные тесты (ряды, теория вероятностей, математическая статистика)	Составитель: Лаврусь О.Е.
ВАРИАНТ 3	Лаврусь В.В.

	1. Дан знакоположительный числовой ряд	∞	a		. Тогда	lim n a		= p	называется
		∑		n			n
						n→∞
		n=1
	достаточным признаком:

A)Даламбера;

B)сравнения;

C)Маклорена;

D)радикальным Коши.

∞

n

n

2. Третий член ряда ∑

(−1)

3

равен:

2

n=1

(2n −1)

A) – 0,75;

B) 1,08;

C) – 1,08;

D) 1,5.

1

2

3

3. n-й член ряда

+

+

+ … равен:

3!

2!

4!

∞

n + 1

A) ∑

;

(n + 2)!

n=1

∞

n

B) ∑

;

(n + 1)!

n=0

∞

n

C) ∑

;

(n + 1)!

n=1

∞

n + 1

D) ∑

.

(n + 1)!

n=1

∞

n

4. Сумма первых трех членов ряда ∑

(− 1) n

равна:

2

n=1

n + 1

A) – 0,4;

D) 0,5;

C) – 0,8;

D) – 0,3.

∞

n+1

5. Найти интервал сходимости функционального ряда ∑

(x + 1)

:

n

n=1

3

A)– 3 < x < 3;

B)– 2 < x < 4;

C)– 1 < x < 1;

D)– 4 < x < 2.

6. Вероятность появления одного из двух несовместных событий А и В, безразлично какого, равна:

A)Р(А + В) = Р(А)·Р(В);

B)Р(А + В) = Р(А) + Р(В);

C)Р(А + В) = Р(А) + Р(В) – Р(АB);

D)Р(А + В) = Р(A) + Р(B) + Р(AВ).

7. Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B1, B2, …, Bn, образующих полную группу, находится по формуле:

A)Бернулли;

B)Пуассона;

C)полной вероятности;

D)Байеса.

8. Игральная кость бросается один раз. Найти вероятность того, что выпадет не более четырех очков.

A)2/3;

B)1/3;

C)5/6;

D)1/6.

9. Монету бросают 3 раза. Найти вероятность того, что «герб» выпадет ровно 1 раз.

A)0,375;

B)0,5;

C)0,125;

D)0,25.

10. Вероятность наступления события A в каждом испытании равна 0,5. Вероятность того, что в результате проведения 300 независимых испытаний событие A наступит не менее 100 раз, вычисляется:

A)по локальной формуле Муавра-Лапласа;

B)по интегральной формуле Лапласа;

C)по формуле Бернулли;

D)по формуле Пуассона.

11. Математическое ожидание постоянной величины C:

A)равно нулю;

B)не существует;

C)равно самой постоянной C;

D)равно единице.

12. Дискретная случайная величина X задана законом распределения:

xi	0	3	6
pi	0,4	p2	0,2

Математическое ожидание M(X) этой случайной величины равно:

A)0,4;

B)2,4;

C)3,6;

D)1,8.

ВАРИАНТ 3

13.Найти дисперсию случайной величины Z = 2X – 2, если известна дисперсия случайной величины X: D(X) = 2.

A) 10; B) 4; C) 6; D) 8.

14.Случайная величина X задана интегральной функцией:

	0			при x ≤ 6;
	x
	F(x)=		− 2	при 6 < x ≤ 9;
		3
				при x > 9.
	1

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (7, 8).

A)3/4;

B)1/3;

C)2/3;

D)1/4.

15. Дана дифференциальная функция случайной величины X:

0 при x ≤ 0;

f (x)= 3x2 при 0 < x ≤ 1;

0 при x > 1.

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (0; 0,5).

A)0,125;

B)0,35;

C)0,875;

D)0,375.

16. Случайная величина X задана интегральной функцией:

0				при x ≤ −1;
x3 + 1
F(x)=				при − 1 < x	≤ 2;
		γ
1				при x > 2.

Коэффициент γ равен:

A)2;

B)5;

C)9;

D)7.

17. Найти моду статистической выборки

3, 1, 2, 3, 5, 2, 1, 2, 4, 5, 4.

A)2;

B)5;

C)1;

D)3.

18. Если основная гипотеза имеет вид H0: a = 5, то конкурирующей может быть гипотеза:

A)Н1: a ≤ 5;

B)Н1: a ≠ 4;

C)Н1: a < 5;

D)Н1: a ≥ 4.

19.Точечная оценка математического ожидания случайной величины, распределенной по нормальному закону, равна 8. Тогда его интервальная оценка может быть записана в виде:

A) (8,4; 9,4); B) (7,6; 8,4); C) (7; 8,5); D) (7,5; 8).

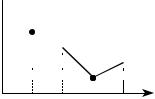
20.Из генеральной совокупности извлечена выборка объема n = 50, полигон относительных частот которой имеет вид

wi

0,3 0,2 0,1

0

3

6

9

12 xi .

Тогда число вариант x1 = 3 в выборке равно:

A)25;

B)15;

C)18;

D)20;

21. Выборочное уравнение парной регрессии имеет вид y = 6 – 1,2x. Тогда выборочный коэффициент корреляции может быть равен:

A)– 5;

B)– 1,2;

C)– 0,8;

D)0.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика)	Составитель: Лаврусь О.Е.
ВАРИАНТ 4	Лаврусь В.В.

1. Рассматривается сходимость знакоположительного числового ряда по формуле

lim an+1 = p . Тогда справедливо утверждение, что ряд сходится при

n→∞ an

A)p = 1;

B)p > 1;

C)p < 1;

D)p = 2.

∑∞ n2

2. Третий член ряда n=1 8n2 + 1 равен:

A)0,125;

B)9/217;

C)9/73;

D)1/9.

3. n-й член ряда

1

−

2

+

3

+ … равен:

2!

4!

3!

∞

n

A) ∑(−

1)n

;

(n

n=1

+ 1)!

∞

n

B) ∑(−

1)n−1

;

(n +

1)!

n=1

∞

1

C) ∑(−

1)n

;

n!

n=1

∞

n + 1

D) ∑(−

1)n

.

n=1

(n + 2)!

∞

n+1

4. Сумма первых трех членов ряда ∑

(− 1)

равна:

2n + 1

n=1

A)

21

;

B)

29

;

C) –

29

;

D)

33

.

105

105

105

105

∑∞ (x + 1)n

5. Найти интервал сходимости функционального ряда − :

n=1 2n 1

A)– 3 < x < 1;

B)– 2 < x < 2;

C)– 4 < x < 0;

D)1 < x < 3.

6. Сумма вероятностей событий А1, А2, А3, образующих полную группу, равна:

A)0,33;

B)0,5;

C)1;

D)0.7.

7. Формула Pn (m)= Cnm pm qn−m называется формулой:

A)Пуассона;

B)Лапласа;

C)Бернулли;

D)полной вероятности.

8.Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,8; третий – 0,7. Найти вероятность того, что студент сдаст только второй экзамен.

A) 0,054; B) 0,333; C) 0,024; D) 0,994.

9.В семье 5 детей. Считая вероятность рождения мальчика и девочки равными между собой, найти вероятность того, что в данной семье 3 девочки.

A) 5/16;

B)3/5;

C)5/32;

D)3/16.

10. Вероятность наступления события A в каждом испытании равна 0,25. Вероятность того, что в результате проведения 243 независимых испытаний событие A наступит ровно 70 раз, вычисляется:

A) по формуле Бернулли;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа; D) по формуле Пуассона.

11. Постоянный множитель C выносится за знак математического ожидания по формуле:

A) M (CX )= M (X ) ; C

B) M(CX) = C2·M(X);

C) M(CX) = C·M(X);

D) M (CX )= M (X ) . C2

12. Дискретная случайная величина X принимает значения 7, – 2, 1, – 5, 3 с равными вероятностями. Математическое ожидание M(X) этой случайной величины равно:

A)0,4;

B)0,8;

C)0,6;

D)0,9.

ВАРИАНТ 4

13.Найти математическое ожидание случайной величины Z = 2X + 5Y – 1, если известны математические ожидания независимых случайных величин X и Y: M(X) = 1,5;

M(Y) = 2.

A) 12; B) 13; C) 14; D) 15.

14.Случайная величина X задана интегральной функцией:

0 при x ≤0;

F(x)= x2 при 0 < x ≤6;

36

1 при x >6.

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (0, 2).

A)1/9;

B)2/9;

C)4/9;

D)5/9.

15. Дана дифференциальная функция случайной величины X:

0			при x ≤0;
	3x2
f (x)=			при 0 < x ≤ 2;
		8
			при x > 2.
0

Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (0, 1).

A)1/8;

B)3/8;

C)5/8;

D)7/8.

16. Дана дифференциальная функция случайной величины X:

0 при x ≤0;

f (x)= 2x при 0 < x ≤ β ;9

0 при x > β .

Коэффициент β равен:

A)1;

B)3;

C)5;

D)9.

17. Найти моду статистической выборки

2, 4, 1, 4, 1, 3, 3, 4, 5, 2, 5.

A) 5;

B) 4;

C) 3;

D) 2.

18.. Если основная гипотеза имеет вид H0: a = 7, то конкурирующей может быть гипотеза:

A)Н1: a ≠ 6;

B)Н1: a > 7

C)Н1: a ≤ 7;

D)Н1: a ≥ 7.

19. Точечная оценка математического ожидания случайной величины, распределенной по нормальному закону, равна 9. Тогда его интервальная оценка может быть записана в виде:

A)(8,6; 9,5);

B)(8,5; 9,4);

C)(7,5; 10,5);

D)(7; 10).

20. Из генеральной совокупности извлечена выборка объема n = 90, полигон относительных частот которой имеет вид

wi
0,4
0,3
0,1
0	4	8	12	16 xi .

Тогда число вариант x3 = 12 в выборке равно:

A)16;

B)12;

C)18;

D)20;

21. Выборочное уравнение парной регрессии имеет вид y = 2x – 0,8. Тогда выборочный коэффициент корреляции может быть равен:

A)2;

B)– 0,8;

C)0,8;

D)– 0,4.