Алгоритмы C++

Даны два массива

и

одной длины . Требуется вывести значения каждого скалярного произведения вектора

на очередной циклический сдвиг вектора .

Инвертируем массив 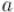и припишем к нему в конец 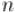нулей, а к массиву — просто припишем самого себя.

Затем перемножим их как многочлены за

. Теперь рассмотрим кожффициенты

произведения 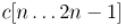(как всегда, все индексы в 0-индексации). Имеем:

Поскольку все элементы 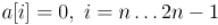, то мы получаем:

Нетрудно увидеть в этой сумме, что это именно скалярное произведение вектора на	-ый циклический
сдвиг. Таким образом, эти коэффициенты — и есть ответ на задачу.
Две полоски
Даны две полоски, заданные как два булевских (т.е. числовых со значениями 0 или 1) массива	и . Требуется

найти все такие позиции на первой полоске, что если приложить, начиная с этой позиции, вторую полоску, ни в каком месте не получится сразу на обеих полосках. Эту задачу можно переформулировать таким образом: дана карта полоски, в виде 0/1 — можно вставать в эту клетку или нет, и дана некоторая фигурка в виде шаблона (в виде массива, в котором 0 — нет клетки, 1 — есть), требуется найти все позиции в полоске, к которым можно приложить фигурку.

Эта задача фактически ничем не отличается от предыдущей задачи — задачи о скалярном произведении. Действительно, скалярное произведение двух 0/1 массивов — это количество элементов, в которых одновременно оказались единицы. Наша задача в том, чтобы найти все циклические сдвиги второй полоски так, чтобы не нашлось ни одного элемента, в котором бы в обеих полосках оказались единицы. Т.е. мы должны найти все циклические сдвиги второго массива, при которых скалярное произведение равно нулю.

Таким образом, и эту задачу мы решили за .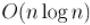

Поиск в ширину

Поиск в ширину (обход в ширину, breadth-first search) — это один из основных алгоритмов на графах.

В результате поиска в ширину находится путь кратчайшей длины в невзвешененном графе, т.е. путь, содержащий наименьшее число рёбер.

Алгоритм работает за 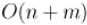, где 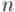— число вершин, 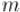— число рёбер.

Описание алгоритма

На вход алгоритма подаётся заданный граф (невзвешенный), и номер стартовой вершины . Граф может быть как ориентированным, так и неориентированным, для алгоритма это не важно.

Сам алгоритм можно понимать как процесс "поджигания" графа: на нулевом шаге поджигаем только вершину 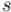. На каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей; т.е. за одну итерацию алгоритма происходит расширение "кольца огня" в ширину на единицу (отсюда и название алгоритма).

Более строго это можно представить следующим образом. Создадим очередь , в которую будут помещаться горящие вершины, а также заведём булевский массив , в котором для каждой вершины будем отмечать, горит

она уже или нет (или иными словами, была ли она посещена).

Изначально в очередь помещается только вершина , и		, а для всех остальных
вершин	. Затем алгоритм представляет собой цикл: пока очередь не пуста, достать из её головы

одну вершину, просмотреть все рёбра, исходящие из этой вершины, и если какие-то из просмотренных вершин ещё не горят, то поджечь их и поместить в конец очереди.

В итоге, когда очередь опустеет, обход в ширину обойдёт все достижимые из 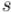вершины, причём до каждой дойдёт кратчайшим путём. Также можно посчитать длины кратчайших путей (для чего просто надо завести массив длин путей ), и компактно сохранить информацию, достаточную для восстановления всех этих кратчайших путей

(для этого надо завести массив "предков" , в котором для каждой вершины хранить номер вершины, по которой мы попали в эту вершину).

Реализация

Реализуем вышеописанный алгоритм на языке C++.

Входные данные:

vector < vector<int> > g; // граф int n; // число вершин

int s; // стартовая вершина (вершины везде нумеруются с нуля)

// чтение графа

...

Сам обход:

queue<int> q; q.push (s);

vector<bool> used (n); vector<int> d (n), p (n); q[t++] = s;

used[s] = true; p[s] = -1;

while (!q.empty()) { int v = q.front(); q.pop();

for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i];

if (!used[to]) { used[to] = true; q.push (to); d[to] = d[v] + 1; p[to] = v;

}

}

}

Если теперь надо восстановить и вывести кратчайший путь до какой-то вершины 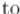, это можно сделать следующим образом:

if (!used[to])

cout << "No path!"; else {

vector<int> path;

for (int v=to; v!=-1; v=p[v]) path.push_back (v);

reverse (path.begin(), path.end()); cout << "Path: ";

for (size_t i=0; i<path.size(); ++i) cout << path[i] + 1 << " ";

}

Приложения алгоритма

●Поиск кратчайшего пути в невзвешенном графе.

●Поиск компонент связности в графе за .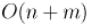

Для этого мы просто запускаем обход в ширину от каждой вершины, за исключением вершин, оставшихся

посещёнными (	) после предыдущих запусков. Таким образом, мы выполняем обычный запуск в ширину
от каждой вершины, но не обнуляем каждый раз массив		, за счёт чего мы каждый раз будем обходить
новую компоненту связности, а суммарное время работы алгоритма составит по-прежнему			(такие
несколько запусков обхода на графе без обнуления массива		называются серией обходов в ширину).

●Нахождения решения какой-либо задачи (игры) с наименьшим числом ходов, если каждое состояние системы можно представить вершиной графа, а переходы из одного состояния в другое — рёбрами графа.

Классический пример — игра, где робот двигается по полю, при этом он может передвигать ящики, находящиеся на этом же поле, и требуется за наименьшее число ходов передвинуть ящики в требуемые позиции. Решается это обходом

в ширину по графу, где состоянием (вершиной) является набор координат: координаты робота, и координаты всех коробок.

●Нахождение кратчайшего пути в 0-1-графе (т.е. графе взвешенном, но с весами равными только 0 либо 1): достаточно немного модифицировать поиск в ширину: если текущее ребро нулевого веса, и происходит улучшение расстояния до какой-то вершины, то эту вершину добавляем не в конец, а в начало очереди.

●Нахождение кратчайшего цикла в неориентированном невзвешенном графе: производим поиск в ширину из каждой вершины; как только в процессе обхода мы пытаемся пойти из текущей вершины по какому-то ребру в уже посещённую вершину, то это означает, что мы нашли кратчайший цикл, и останавливаем обход в ширину; среди всех таких найденных циклов (по одному от каждого запуска обхода) выбираем кратчайший.

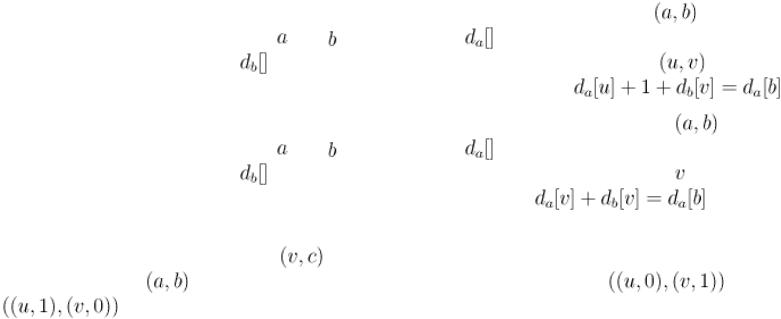
●	Найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин				. Для
	этого надо запустить 2 поиска в ширину: из	, и из	. Обозначим через	массив кратчайших расстояний, полученный
	в результате первого обхода, а через	— в результате второго обхода. Теперь для любого ребра
	легко проверить, лежит ли он на каком-либо кратчайшем пути: критерием будет условие				.
●	Найти все вершины, лежащие на каком-либо кратчайшем пути между заданной парой вершин				. Для
	этого надо запустить 2 поиска в ширину: из	, и из	. Обозначим через	массив кратчайших расстояний, полученный
	в результате первого обхода, а через	— в результате второго обхода. Теперь для любой вершины			легко
	проверить, лежит ли он на каком-либо кратчайшем пути: критерием будет условие				.

●Найти кратчайший чётный путь в графе (т.е. путь чётной длины). Для этого надо построить вспомогательный граф, вершинами которого будут состояния , где 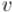— номер текущей вершины, 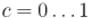— текущая

чётность. Любое ребро		исходного графа в этом новом графе превратится в два ребра
и	. После этого на этом графе надо обходом в ширину найти кратчайший путь из стартовой вершины

в конечную, с чётностью, равной 0.

Поиск в глубину

Это один из основных алгоритмов на графах.

В результате поиска в глубину находится лексикографически первый путь в графе. Алгоритм работает за O (N+M).

Применения алгоритма

●Поиск любого пути в графе.

●Поиск лексикографически первого пути в графе.

●Проверка, является ли одна вершина дерева предком другой:

В начале и конце итерации поиска в глубину будет запоминать "время" захода и выхода в каждой вершине. Теперь за O

(1) можно найти ответ: вершина i является предком вершины j тогда и только тогда, когда starti < startj и endi > endj.

●Задача LCA (наименьший общий предок).

●Топологическая сортировка:

Запускаем серию поисков в глубину, чтобы обойти все вершины графа. Отсортируем вершины по времени выхода по убыванию - это и будет ответом.

●Проверка графа на ацикличность и нахождение цикла

●Поиск компонент сильной связности:

Сначала делаем топологическую сортировку, потом транспонируем граф и проводим снова серию поисков в глубину в порядке, определяемом топологической сортировкой. Каждое дерево поиска - сильносвязная компонента.

●Поиск мостов:

Сначала превращаем граф в ориентированный, делая серию поисков в глубину, и ориентируя каждое ребро так, как мы пытались по нему пройти. Затем находим сильносвязные компоненты. Мостами являются те рёбра, концы которых принадлежат разным сильносвязным компонентам.

Реализация

vector < vector<int> > g; // граф int n; // число вершин

vector<int> color; // цвет вершины (0, 1, или 2)

vector<int> time_in, time_out; // "времена" захода и выхода из вершины int dfs_timer = 0; // "таймер" для определения времён

void dfs (int v) {

time_in[v] = dfs_timer++; color[v] = 1;

for (vector<int>::iterator i=g[v].begin(); i!=g[v].end(); ++i) if (color[*i] == 0)

dfs (*i);

color[v] = 2;

time_out[v] = dfs_timer++;

}

Это наиболее общий код. Во многих случаях времена захода и выхода из вершины не важны, так же как и не важны цвета вершин (но тогда надо будет ввести аналогичный по смыслу булевский массив used). Вот наиболее

простая реализация:

vector < vector<int> > g; // граф int n; // число вершин

vector<char> used;

void dfs (int v) { used[v] = true;

for (vector<int>::iterator i=g[v].begin(); i!=g[v].end(); ++i) if (!used[*i])

dfs (*i);

}

Топологическая сортировка

Быстрее всего эту задачу можно решить с помощью поиска в глубину - за O (N+M).

Алгоритм

Произведём серию поисков в глубину, чтобы посетить весь граф. Отсортируем вершины по убыванию времени выхода - это и будет ответом.

Вместо сортировки можно просто сделать вектор ans, который будет изначально пустым, и добавлять в него текущую вершину v при возврате из текущей вершины. В таком случае вообще времена выхода в явном виде не потребуются.

Реализация

vector < vector<int> > g; // граф int n; // число вершин

vector<bool> used;

vector<int> ans;

void dfs (int v)

{

used[v] = true;

for (vector<int>::itetator i=g[v].begin(); i!=g[v].end(); ++i) if (!used[*i])

dfs (*i); ans.push_back (v);

}

void topological_sort (vector<int> & result)

{

used.assign (n, false);

for (int i=0; i<n; ++i) if (!used[i])

dfs (i);

result = ans;

}

Поиск компонент связности

Эта задача элементарно решается с помощью поиска в глубину или в ширину. Алгоритм работает за O (N+M).

Алгоритм

Просто производим серию поисков в глубину (в ширину), чтобы посетить все вершины графа. Каждое дерево поиска и будет содержать отдельную компоненту связности.

Реализация

Код на основе поиска в ширину:

void find_connected_components (const vector < vector<int> > & g, int n)

{

vector<bool> used (n); cout << "Components:\n"; for (int v=0; v<n; ++v)

if (!used[v])

{

cout << "[ " << v; vector<int> q (n); int h=0, t=0; q[t++] = v; used[v] = true; while (h < t)

{

int cur = q[h++];

for (vector<int>::iterator i=g[cur].begin();

i!=g[cur].end(); ++i)

if (!used[*i])

{

used[*i] = true; q[t++] = *i;