Алгоритмы C++
.pdf
Наименьший общий предок. Нахождение за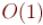 
в оффлайн (алгоритм Тарьяна)
Дано дерево |
с вершинами и дано |
запросов вида |
. Для каждого запроса |
требуется |
найти наименьшего общего предка вершин |
и , т.е. такую вершину , которая наиболее удалена от корня дерева, |
|||
и при этом является предком обеих вершин |
и . |
|
|
|
Мы рассматриваем задачу в режиме оффлайн, т.е. считая, что все запросы известны заранее. Описываемый |
||||
ниже алгоритм позволяет ответить на все |
запросов за суммарное время |
, т.е. при достаточно большом |
||
за |
на запрос. |
|
|
|
Алгоритм Тарьяна
Основой для алгоритма является структура данных "Система непересекающихся множеств", которая и была изобретена Тарьяном (Tarjan).
Алгоритм фактически представляет собой обход в глубину из корня дерева, в процессе которого постепенно
находятся ответы на запросы. А именно, ответ на запрос |
находится, когда обход в глубину находится в вершине |
, а вершина уже была посещена, или наоборот. |
|
Итак, пусть обход в глубину находится в вершине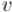 
(и уже были выполнены переходы в её сыновей), и оказалось, что
для какого-то запроса |
вершина уже была посещена обходом в глубину. Научимся тогда находить |
||
этих двух вершин. |
|
|
|
Заметим, что |
|
является либо самой вершиной , либо одним из её предков. Получается, нам надо |
|
найти самую нижнюю вершину среди предков (включая её саму), для которой вершина |
является потомком. |
||
Заметим, что при фиксированном по такому признаку (т.е. какой наименьший предок |
является и предком какой- |
||
то вершины) вершины дерева дерева распадаются на совокупность непересекающихся классов. Для каждого |
|||
предка |
вершины |
её класс содержит саму эту вершину, а также все поддеревья с корнями в тех её |
|
сыновьях, которые лежат "слева" от пути до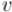 
(т.е. которые были обработаны ранее, чем была достигнута 
).
Нам надо научиться эффективно поддерживать все эти классы, для чего мы и применим структуру данных "Система непересекающихся множеств". Каждому классу будет соответствовать в этой структуре множество, причём для представителя этого множества мы определим величину 
— ту вершину 
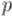, которая и образует
этот класс. |
|
|
|
|
Рассмотрим подробно реализацию обхода в глубину. Пусть мы стоим в некоторой вершине |
. Поместим её в |
|||
отдельный класс в структуре непересекающихся множеств, |
. Как обычно в обходе в |
|||
глубину, перебираем все исходящие рёбра |
. Для каждого такого |
мы сначала должны вызвать обход в |
||
глубину из этой вершины, а потом добавить эту вершину со всем её поддеревом в класс вершины . Это |
||||
реализуется операцией |
структуры данных "система непересекающихся множеств", с последующей |
|||
установкой |
для представителя множества (т.к. после объединения представитель класса |
|||
мог измениться). Наконец, после обработки всех рёбер мы перебираем все запросы вида |
, и если |
|||
была помечена как посещённая обходом в глубину, то ответом на этот запрос будет |
|
|||
вершина |
|
. Нетрудно заметить, что для каждого запроса это |
||
условие (что одна вершина запроса является текущей, а другая была посещена ранее) выполнится ровно один раз.
Оценим асимптотику. Она складывается из нескольких частей. Во-первых, это асимптотика обхода в глубину, которая в данном случае составляет . Во-вторых, это операции по объединению множеств, которые в сумме
для всех разумных затрачивают |
операций. В-третьих, это для каждого запроса проверка условия (два раза |
|||
на запрос) и определение результата (один раз на запрос), каждое, опять же, для всех разумных |
|
выполняется за |
||
|
. Итоговая асимптотика получается |
, что означает для достаточно больших |
( |
) ответ |
за |
на один запрос. |
|
|
|
Реализация
Приведём полную реализацию данного алгоритма, включая слегка изменённую (с поддержкой 
) реализацию системы пересекающихся множеств (рандомизированный варианта).
const int MAXN = максимальное число вершин в графе; vector<int> g[MAXN], q[MAXN]; // граф и все запросы int dsu[MAXN], ancestor[MAXN];
bool u[MAXN];
int dsu_get (int v) {
return v == dsu[v] ? v : dsu[v] = dsu_get (dsu[v]);
}
void dsu_unite (int a, int b, int new_ancestor) { a = dsu_get (a), b = dsu_get (b);
if (rand() & 1) swap (a, b);
dsu[a] = b, ancestor[b] = new_ancestor;
}
void dfs (int v) {
dsu[v] = v, ancestor[v] = v; u[v] = true;
for (size_t i=0; i<g[v].size(); ++i) if (!u[g[v][i]]) {
dfs (g[v][i]);
dsu_unite (v, g[v][i], v);
}
for (size_t i=0; i<q[v].size(); ++i) if (u[q[v][i]]) {
printf ("%d %d -> %d\n", v+1, q[v][i]+1, ancestor[ dsu_get(q[v][i]) ]+1);
}
int main() {
... чтение графа ...
//чтение запросов for (;;) {
int a, b = ...; // очередной запрос
--a, --b; q[a].push_back (b); q[b].push_back (a);
}
//обход в глубину и ответ на запросы dfs (0);
}
Максимальный поток методом Эдмондса-Карпа за O (N M2)
Пусть дан граф G, в котором выделены две вершины: исток S и сток T, а у каждого ребра определена
пропускная способность Cu,v. Поток F можно представить как поток вещества, которое могло бы пройти по сети от истока к стоку, если рассматривать граф как сеть труб с некоторыми пропускными способностями. Т.е. поток - функция Fu,
v, определённая на множестве рёбер графа.
Задача заключается в нахождении максимального потока. Здесь будет рассмотрен метод Эдмондса-Карпа, работающий за O (N M2), или (другая оценка) O (F M), где F - величина искомого потока. Алгоритм был предложен в 1972 году.
Алгоритм
Остаточной пропускной способностью называется пропускная способность ребра за вычетом текущего потока вдоль этого ребра. При этом надо помнить, что если некоторый поток протекает по ориентированному ребру, то возникает так называемое обратное ребро (направленное в обратную сторону), которое будет иметь нулевую пропускную способность, и по которому будет протекать тот же по величине поток, но со знаком минус. Если же ребро было неориентированным, то оно как бы распадается на два ориентированных ребра с одинаковой
пропускной способностью, и каждое из этих рёбер является обратным для другого (если по одному протекает поток F, то по другому протекает -F).
Общая схема алгоритма Эдмондса-Карпа такова. Сначала полагаем поток равным нулю. Затем
ищем дополняющий путь, т.е. простой путь из S в T по тем рёбрам, у которых остаточная пропускная способность строго положительна. Если дополняющий путь был найден, то производится увеличение текущего потока вдоль этого пути. Если же пути не было найдено, то текущий поток является максимальным. Для поиска дополняющего пути может использоваться как Обход в ширину, так и Обход в глубину.
Рассмотрим более точно процедуру увеличения потока. Пусть мы нашли некоторый дополняющий путь, тогда пусть C - наименьшая из остаточных пропускных способностей рёбер этого пути. Процедура увеличения потока заключается
в следующем: для каждого ребра (u, v) дополняющего пути выполним: Fu, v += C, а Fv, u = - Fu, v (или, что то же самое, Fv, u
-= C).
Величиной потока будет сумма всех неотрицательных величин FS, v, где v - любая вершина, соединённая с истоком.
Реализация
const int inf = 1000*1000*1000;
typedef vector<int> graf_line; typedef vector<graf_line> graf;
typedef vector<int> vint; typedef vector<vint> vvint;
int main()
{
int n; cin >> n;
vvint c (n, vint(n)); for (int i=0; i<n; i++)
for (int j=0; j<n; j++) cin >> c[i][j];
// исток - вершина 0, сток - вершина n-1
vvint f (n, vint(n)); for (;;)
{
vint from (n, -1); vint q (n);
int h=0, t=0; q[t++] = 0; from[0] = 0;
for (int cur; h<t;)
{
cur = q[h++];
for (int v=0; v<n; v++)
if (from[v] == -1 && c[cur][v]-f[cur][v] > 0)
{
q[t++] = v; from[v] = cur;
}
}
if (from[n-1] == -1) break;
int cf = inf;
for (int cur=n-1; cur!=0; )
{
int prev = from[cur];
cf = min (cf, c[prev][cur]-f[prev][cur]); cur = prev;
}
for (int cur=n-1; cur!=0; )
{
int prev = from[cur]; f[prev][cur] += cf; f[cur][prev] -= cf; cur = prev;
}
}
int flow = 0;
for (int i=0; i<n; i++) if (c[0][i])
flow += f[0][i];
cout << flow;
}
Максимальный поток методом Проталкивания предпотока за O (N4)
Пусть дан граф G, в котором выделены две вершины: исток S и сток T, а у каждого ребра определена
пропускная способность Cu,v. Поток F можно представить как поток вещества, которое могло бы пройти по сети от истока к стоку, если рассматривать граф как сеть труб с некоторыми пропускными способностями. Т.е. поток - функция Fu,
v, определённая на множестве рёбер графа.
Задача заключается в нахождении максимального потока. Здесь будет рассмотрен метод Проталкивания предпотока, работающий за O (N4), или, точнее, за O (N2 M). Алгоритм был предложен Гольдбергом в 1985 году.
Алгоритм
Общая схема алгоритма такова. На каждом шаге будем рассматривать некоторый предпоток - т.е. функцию, которая по свойствам напоминает поток, но не обязательно удовлетворяет закону сохранения потока. На каждом шаге будем пытаться применить какую-либо из двух операций: проталкивание потока или поднятие вершины. Если на какомто шаге станет невозможно применить какую-либо из двух операций, то мы нашли требуемый поток.
Для каждой вершины определена её высота Hu, причём HS = N, HT = 0, и для любого остаточного ребра (u, v) имеем Hu
<= Hv + 1.
Для каждой вершины (кроме S) можно определить её избыток: Eu = FV, u. Вершина с положительным избытком называется переполненной.
Операция проталкивания Push (u, v) применима, если вершина u переполнена, остаточная пропускная способность Cfu, v > 0 и Hu = Hv + 1. Операция проталкивания заключается в максимальном увеличении потока из u в v,
ограниченном избытком Eu и остаточной пропускной способностью Cfu, v.
Операция поднятия Lift (u) поднимает переполненную вершину u на максимально допустимую высоту. Т.е. Hu = 1 + min { Hv }, где (u, v) - остаточное ребро.
Осталось только рассмотреть инициализацию потока. Нужно инициализировать только следующие значения: FS, v = CS, v, Fu, S = - Cu, S, остальные значения положить равными нулю.
Реализация
const int inf = 1000*1000*1000;
typedef vector<int> graf_line; typedef vector<graf_line> graf;
typedef vector<int> vint; typedef vector<vint> vvint;
void push (int u, int v, vvint & f, vint & e, const vvint & c)
{
int d = min (e[u], c[u][v] - f[u][v]); f[u][v] += d;
f[v][u] = - f[u][v]; e[u] -= d;
e[v] += d;
}
void lift (int u, vint & h, const vvint & f, const vvint & c)
{
int d = inf;
for (int i = 0; i < (int)f.size(); i++) if (c[u][i]-f[u][i] > 0)
d = min (d, h[i]);
if (d == inf) return;
h[u] = d + 1;
}
int main()
{
int n; cin >> n;
vvint c (n, vint(n)); for (int i=0; i<n; i++)
for (int j=0; j<n; j++) cin >> c[i][j];
// исток - вершина 0, сток - вершина n-1
vvint f (n, vint(n)); for (int i=1; i<n; i++)
{
f[0][i] = c[0][i]; f[i][0] = -c[0][i];
}
vint h (n); h[0] = n;
vint e (n);
for (int i=1; i<n; i++) e[i] = f[0][i];
for ( ; ; )
{
int i;
for (i=1; i<n-1; i++) if (e[i] > 0)
break;
if (i == n-1) break;
int j;
for (j=0; j<n; j++)
if (c[i][j]-f[i][j] > 0 && h[i]==h[j]+1) break;
if (j < n)
push (i, j, f, e, c);
else
lift (i, h, f, c);
}
int flow = 0;
for (int i=0; i<n; i++) if (c[0][i])
flow += f[0][i];
cout << max(flow,0);
}