Алгоритмы C++

в котором и	уже будут взаимно просты, а такое уравнение мы уже научились решать. Обозначим его решение
через .
Понятно, что это	будет также являться и решением исходного уравнения. Однако если	, то оно будет
не единственным решением. Можно показать, что исходное уравнение будет иметь ровно		решений, и они
будут иметь вид:

Подводя итог, можно сказать, что количество решений линейного модульного уравнения равно либо , либо нулю.

Решение с помощью Расширенного алгоритма Евклида

Приведём наше модулярное уравнение к диофантову уравнению следующим образом:

где 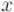и 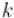— неизвестные целые числа.

Способ решения этого уравнения описан в соответствующей статье Линейные диофантовы уравнения второго порядка, и заключается он в применении Расширенного алгоритма Евклида.

Там же описан и способ получения всех решений этого уравнения по одному найденному решению, и, кстати говоря, этот способ при внимательном рассмотрении абсолютно эквивалентен способу, описанному в предыдущем пункте.

Китайская теорема об остатках

Формулировка

В своей современной формулировке теорема звучит так:

Пусть 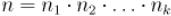, где 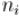— попарно взаимно простые числа.

Поставим в соответствие произвольному числу 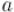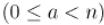кортеж , где :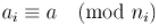

Тогда это соответствие (между числами и кортежами) будет являться взаимно однозначным. И, более того, операции, выполняемые над числом 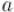, можно эквивалентно выполнять над соответствующими элементами кортежами

— путём независимого выполнения операций над каждым компонентом. Т.е., если

то справедливо:

В своей первоначальной формулировке эта теорема была доказана китайским математиком Сунь-Цзы приблизительно в 100 г. н.э. А именно, он показал в частном случае эквивалентность решения системы модулярных уравнений и решения одного модулярного уравнения (см. следствие 2 ниже).

Следствие 1

Система модулярных уравнений:

имеет единственное решение по модулю .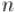

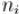(как и выше, , числа попарно взаимно просты, а набор 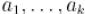— произвольный набор целых чисел)

Следствие 2

Следствием является связь между системой модулярных уравнений и одним соответствующим модулярным уравнением: Уравнение:

эквивалентно системе уравнений:

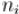(как и выше, предполагается, что , числа попарно взаимно просты, а 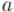— произвольное целое число)

Алгоритм Гарнера

Из китайской теоремы об остатках следует, что можно заменять операции над числами операциями над кортежами. Напомним, каждому числу 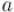ставится в соответствие кортеж , где:

Это может найти широкое применение на практике, поскольку мы таким образом можем заменять операции в длинной арифметике операциями с массивом "коротких" чисел. Скажем, массива из 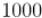элементов "хватит" на

числа примерно с	знаками (если выбрать в качестве -ых первые	простых); а если выбирать в качестве
-ых простые около миллиарда, то тогда хватит уже на число с примерно		знаками. Но, разумеется, тогда
нужно научиться восстанавливать число по этому кортежу. Из следствия 1 видно, что такое
восстановление возможно, и притом единственно (при условии		). Алгоритм Гарнера

и является алгоритмом, позволяющим выполнить это восстановление, причём достаточно эффективно. Будем искать решение в виде:

т.е. в смешанной системе счисления.

Обозначим через

,

) число, являющееся обратным для

по модулю

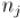(нахождение обратных элементов в кольце по модулю описано здесь:

Подставим выражение в смешанной системе счисления в первое уравнение системы, получим:

Подставим теперь выражение во второе уравнение:

Преобразуем это выражение, отняв от обеих частей 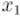и разделив на :

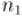Подставляя в третье уравнение, аналогичным образом получаем:

Уже достаточно ясно видна закономерность, которую проще всего выразить кодом:

for (int i=0; i<k; ++i) { x[i] = a[i];

for (int j=0; j<i; ++j) {

x[i] = r[j][i] * (x[i] - x[j]) % n[i]; if (x[i] < 0) x[i] += n[i];

}

}

Итак, мы научились вычислять коэффициенты	за время	, сам же ответ — число — можно восстановить
по формуле:

Стоит заметить, что на практике почти всегда вычислять ответ нужно с помощью Длинной арифметики, но при этом

сами коэффициенты по-прежнему вычисляются на встроенных типах, а потому весь алгоритм Гарнера является весьма эффективным.

Реализация алгоритма Гарнера

Удобнее всего реализовывать этот алгоритм на языке Java, поскольку она содержит стандартную длинную арифметику, а потому не возникает никаких проблем с переводом числа из модульной системы в обычное число

(используется стандартный класс BigInteger).

На C++ всё гораздо сложнее, поскольку длинная арифметика отсутствует, а потому для чтения длинных чисел в десятичной системе, для перевода из модульной системы в десятичную, и для вывода десятичных чисел приходится реализовывать собственную длинную арифметику. Поэтому приведём здесь полную реализацию этого алгоритма на С++, но разделив её на две части: первая — собственно алгоритм Гарнера, а вторая — реализация обычной десятичной длинной арифметики.

Приведённая ниже реализация алгоритма Гарнера поддерживает сложение, вычитание и умножение, причём поддерживает работу с отрицательными числами. Реализовано чтение длинного числа, перевод числа из модулярной системы в длинное число и вывод его.

О поддержке отрицательных чисел следует сказать особо. При чтении длинных чисел знак заносится в глобальную переменную (поскольку в векторе в моей реализации длинной арифметики нет

никакой возможности сохранить его). Далее, сама модулярная схема не предполагает различий между положительными и отрицательными числами. Однако можно заметить, что, если результат по модулю не превосходит половины от произведения всех простых, то при вычислении результата положительные числа получатся меньше этой середины,

а отрицательные — больше. Поэтому мы после классического алгоритма Гарнера сравниваем результат с серединой,

иесли он больше, то выводим минус, и инвертируем результат (т.е. отнимаем его от произведения всех простых,

ивыводим уже его).

typedef vector<int> lnum; bool last_neg;

const int sz = 351; int pr[sz];

int rev[sz][sz];

struct number { short a[sz];

number() {

memset (a, 0, sizeof a);

}

number (const lnum & num) { for (int i=0; i<sz; ++i) {

a[i] += rt.a[i];

if (a[i] >= pr[i]) a[i] -= pr[i];

}

}

void operator-= (const number & rt) { for (int i=0; i<sz; ++i) {

a[i] -= rt.a[i];

if (a[i] < 0) a[i] += pr[i];

}

}

void operator*= (const number & rt) { for (int i=0; i<sz; ++i)

a[i] = ((int)a[i] * rt.a[i]) % pr[i];

}

void negate() {

for (int i=0; i<sz; ++i)

a[i] = a[i] ? pr[i] - a[i] : 0;

}

operator lnum() const { lnum res, cur (1,1); vector<int> x (sz); for (int i=0; i<sz; ++i) {

x[i] = a[i];

for (int j=0; j<i; ++j) {

x[i] = rev[j][i] * (x[i] - x[j]) % pr[i]; if (x[i] < 0) x[i] += pr[i];

}

lnum curadd = cur; multiply (curadd, x[i]); add (res, curadd); multiply (cur, pr[i]);

}

return res;

}

};

ostream & operator<< (ostream & stream, const number & a) { lnum b = a;

lnum t (1, 1);

for (int i=0; i<sz; ++i) multiply (t, pr[i]);

subtract (t, b);

if (compare (t, b) < 0) { printf ("-");

swap (t, b);

}

return stream << b;

}

Реализация необходимых процедур длинной арифметики:

const int base = 1000*1000*1000;

void add (lnum & a, const lnum & b) {

for (int i=0, carry=0; i<(int)max(a.size(),b.size()) || carry; ++i) { if (i == (int)a.size()) a.push_back (0);

a[i] += carry + (i < (int)b.size() ? b[i] : 0); if (a[i] < base)

carry = 0;

else

carry = 1, a[i] -= base;

}

}

void subtract (lnum & a, const lnum & b) { for (int i=0, carry=0; i<(int)a.size(); ++i) {

a[i] -= carry + (i < (int)b.size() ? b[i] : 0); if (a[i] >= 0)

carry = 0;

else

carry = 1, a[i] += base;

}

while (a.size() && !a.back()) a.pop_back();

}

void multiply (lnum & a, int b) {

for (int i=0, carry=0; i<(int)a.size() || carry; ++i) { if (i == (int)a.size()) a.push_back (0);

long long cur = a[i] * 1ll * b + carry; carry = int (cur / base);

a[i] = int (cur - carry * 1ll * base);

}

while (a.size() && !a.back()) a.pop_back();

}

int modulus (const lnum & a, int b) { int carry = 0;

for (int i=(int)a.size()-1; i>=0; --i)

carry = int ((a[i] + carry * 1ll * base) % b);

return carry;

}

int compare (const lnum & a, const lnum & b) { if (a.size() != b.size())

return a.size() < b.size() ? -1 : 1; for (int i=(int)a.size()-1; i>=0; --i)

if (a[i] != b[i])

return a[i] < b[i] ? -1 : 1; return 0;

}

istream & operator>> (istream & stream, lnum & a) { static char s[100*1000];

scanf (" %s", s); last_neg = false;

while (s[0] == '-' || s[0] == '+') { if (s[0] == '-')

last_neg = !last_neg; memmove (s, s+1, strlen(s)); if (s[0] == 0)

scanf (" %s", s);

}

size_t len = strlen(s); if (len % 9) {

size_t add = 9 - len%9; memmove (s+add, s, len); memset (s, '0', add);

len += add;

}

for (size_t i=len; i>0; ) { s[i] = 0;

if (i < 9) i = 0;

else

i -= 9;

a.push_back (atoi (s+i));

}

while (a.size() && !a.back()) a.pop_back(); return stream;

}

ostream & operator<< (ostream & stream, const lnum & a) { printf ("%d", a.empty() ? 0 : a.back());

for (int i=(int)a.size()-2; i>=0; --i) printf ("%09d", a[i]);

return stream;

}