Метод наискорейшего спуска

1

Решается задача на безусловный экстремум:

В основе рассматриваемого метода лежит следующая рекуррентная формула:

-для min: (1)

-для max: (2)

Здесь h – градиентный шаг.

2

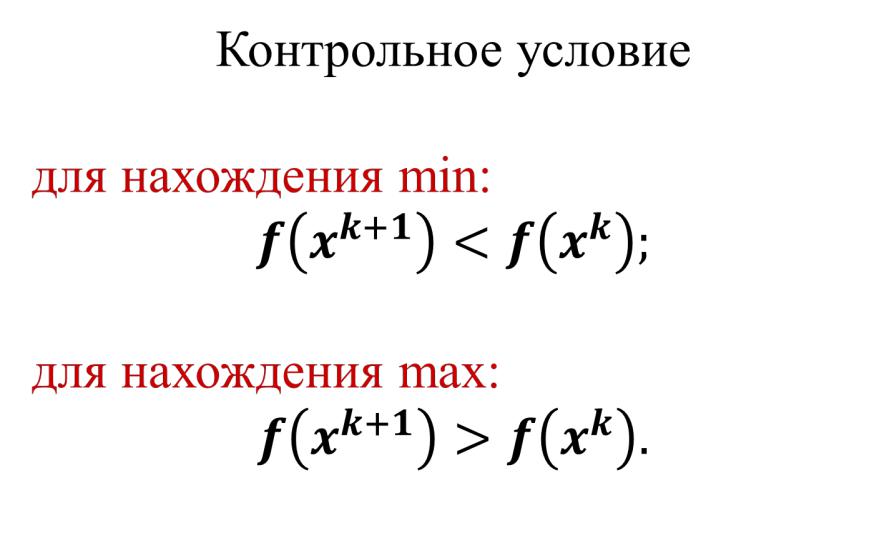
Контрольное условие для нахождения min:

для нахождения max:

3

При практической реализации поиск по указанной схеме (при условии, что на каждом этапе прекращается, если

где	– некоторая заданная	величина,
характеризующая точность		нахождения
минимума (максимума).

Или можно ограничиться условиями:

4

Правильный выбор шага h имеет существенное значение. Чем меньше h, тем точнее результат поиска, но больше вычислений. Причем, если на каком-либо этапе не уменьшается, то это означает, что мы «проскочили» нужную точку. В обычном градиентном методе в этом случае возвращаются к предыдущей точке и уменьшают h вдвое. В методе же наискорейшего спуска h непостоянен и выбирается на каждой итерации.

5

Рассмотрим функцию одного переменного

Найдем h из условия Для этого решим уравнение:

Найденное h подставим в (1) и т. д.

6

Алгоритм метода наискорейшего спуска

1.Находим градиент заданной функции.

2.Задаем точку .

3.Вычисляем.

4. .
5. Подставив координаты точки	в исходную функцию,
получаем

6.Решая уравнение находим h, при котором (h) имеет min.

7.Найденное значение h подставляем в формулу п.4.

8.Сравним значение и .

Необходимо, чтобы . 9. Составим и повторяем п.5-8.

7

Пример 1.

Найти безусловный экстремум

.

Решение:

1. Составим градиент заданной функции:

.

2.Выберем начальную точку В этой точке

3.Градиент в этой точке:

4. Используя формулу (2), запишем:

8

5.Полученные выражения для координат точки х1 подставим в заданную функцию. Тогда

6.Из уравнения имеем .

7.Значит, т.е. и

8.Заметим, что и далее для точки повторим пункты 4-7.

9

и

Получаем

Причем

Взяв получим Следовательно, полученной точке функция достигает максимума.

Ответ: xmax={1;5} и z(xmax)=

10