лекции(II курс)

2) Ò.ê. |X −a| ≤ ε a−ε ≤ X ≤ a+ε, то лемма Чебышева позволяет оценить вероят-

ность попадания случайной величины X в некоторый интервал, причем границы этого интервала должны быть симметричны относительно этого математического ожидания.

Отметим, что если случайная величина X биномиально распределена, то неравенство Чебышева принимает вид

1)					npq
P (|m − np| ≤ ε) ≥ 1			−
							.	(5)
					ε2
2) для частости (доли)					pq
P (|	X	− p| ≤ ε) ≥ 1	−
						.		(6)
	n			nε2

Пример. В среднем 80 процентов студентов заочников работают по специальности. Можно ли с помощью неравенства Чебышева оценить вероятность того, что доля студентов ВУЗа, работающих по специальности заключена в границах 0,7 0,85, если всего в ВУЗе 1500 студентов? Изменить правую границу так, чтобы применение неравенство Чебышева стало возможным, и оченить вероятность с измененной правой границей. Найти приближенное значение той же вероятности с помощью теоремы Муавра Лапласса. Сравнить результаты.

Имеем: p = 0, 8, n = 1500. Оценить вероятность

P (0, 7 < mn < 0, 85).

Воспользуемся формулой (6)

P (|	X	− p| ≤ ε) ≥ 1	−	pq	P (p − ε ≤	X	≤ p + ε) ≥ 1	−	pq
	n			nε2		n			nε2

Заметим, что изначально, границы не являются симметричными относительно математического ожидания, изменим правую границу с 0,85 на 0,9, тогда ε = 0, 1 и можно

пользоваться формулой (6)

P (		X		0, 8	0, 1)		1		0, 8 · 0, 2		1		0, 16			0, 8385.
	| n		−			≥		−	1500(0, 1)2	≥		−	15		≥
				| ≤

Воспользуемся теоремой Муавра Лапласса, а именно следствием 2:

m

n

Pn(|

− p| ≤ ) ≈ Φ( √

).

n

pq

m

n

P (|

− p| < ε) ≈ Φ(ε√

)

n

pq

m

1500

3, 9

P (|

− 0, 8| < 0, 1) ≈ Φ(0, 1√

)

≈ Φ(

) ≈ Φ(6, 7) ≈ 1.

n

0, 8 · 0, 2

4

Вывод: результаты согласуются. Отличие объясняется тем, что интегральная теорема Муавра Лапласса находит приближенное значение вероятности, а неравенство Чебышева производит лишь оценку вероятности.

С помощью неравенства Чебышева можно на только оценивать вероятность P, но и находить значение n, границы изменения величины X, величину отклонения ε.

Пример. Определить количество деталей, необходимое для того, чтобы с вероятностью, не меньшей 0,98, можно было ожидать, что абсолютная величина отклонения доли

41

годных деталей от веротности детали быть годной, равной 0,95 не превысит 0,01 (применить неравенство Чебышева).

p = 0, 95, ε = 0, 01, P ≥ 0, 98 n−?

P (

X

0, 95

0, 01)

1

0, 95 · 0, 05

0, 98

| n

−

≥

≥

| ≤

−

n

·

0, 012

1

0, 95 · 0, 05

0, 98; 1

0, 0475

0, 98;

0, 0475

0, 02;

−

≥

− n

0, 0001

≥

−n

0, 0001

≥ −

n

·

0, 012

·

·

n · 0, 012 ≥ 0, 02 · 0, 0475; n · 0, 0001 ≥ 2, 375; n ≥ 23750.

Таким образом, количество деталей должно быть не менее 23750.

5.3. Теорема Чебышева и ее следствия.

Перейдем к рассмотрению закона больших чисел в форме Чебышева. Так называется теорема Чебышева, являющаяся обобщением его неравенства.

Теорема. Если дисперсии независимых случайных величин X1, X2, . . . , Xn ограничены одной и той же постоянной C, а число их достаточно велико, то, как бы мало ни было данное число ε > 0, вероятность того, что отклонение средней арифмитической

этих случайных величин от средней арифмитической их математических ожиданий не превзойдет ε по абсолютной величине, сколь угодно близка к единице.

P (|

∑nXi

−

∑nai

| ≤ ε) ≥ 1 − δ,

(7)

ãäå δ = C/(nε2).

Доказательство. Применим неравенство Чебышева к случайной величине X = (X1 + X2 + . . . + Xn), являющейся средней арифмитической случайных величин X1, X2, . . . , Xn. Для этого необходмо найти ее математическое ожидание, имеем:

()

	M(X) = M			X1 + X2 + . . . + Xn	=	1	M(X1 + X2 + . . . + Xn) =
				n
						n
	=	1	[M(X1) + M(X2) + . . . + M(Xn)] =					a1 + a2 + . . . + an	,
		n						n

ãäå a1, a2, . . . , an− математические ожидания случайных величин X1, X2, . . . , Xn. Íà îñ- новании свойств дисперсии

()

	X1 + X2 + . . . + Xn	1
D(X) = D		=		D(X1	+ X2 + . . . + Xn).
	n		n2

Случайные величины по условию теоремы независимы. Поэтому к сумме их можно свойство дисперсии (дисперсия суммы есть сумма дисперсий), кроме того, они ограничены одной и той же постоянной C

1

1

1

D(X) =

D(X1 + X2

+ . . . + Xn)

≤

(C + C + . . . + C) =

C.

n2

n2

n

Подставляя в неравенство P (|X − a| ≤ ε) ≥ 1 − D(X)/ε2

выражения X, M(X) è ïîëó-

ченную оценку D(X), имеем

X

X + . . . + X

a + a + . . . + a

C

1 +

2

n

1

2

n

P (

n

−

n

≤ ε) ≥ 1 −

nε2

,

42

èëè	P	(∑nXi		−	∑nai		≤ ε) ≥ 1 − δ.

Вывод:∑ при большом числе n случайных величин практически достоверно, что∑ их средняя xi/n(случайная) как угодно мало отличается от неслучайной величины ai/n

их математического ожидания. В этом и заключен смысл теоремы Чебышева.

Следствие. Если независимые случайные величины имеют одинаковые (равные a) математические ожидания, дисперсии их ограничены одной и той же постоянной C, а число их достаточно велико, то, как бы мало ни было данное число ε > 0, вероят-

ность того, что отклонение средней арифметической этих случайных величин от a не превзойдет по абсолютной величине ε, сколь угодно близка к единице

P	( ∑nxi		− a	≤ ε) ≥ 1 − δ.	(8)

Теорема Бернулли. Если вероятность p наступления события A в каждом из n независимых испытаний постоянна, а число испытаний достаточно велико, то вероятность того, что частость события A будет как угодно мало отличаться от его вероятности, сколь угодно близка к единице, т.е.

( P m

n

	≤ ε) > 1 − δ.
		(9)
− p

Смысл теоремы Бернулли состоит в том, что при большом числе n независимых испытаний практически достоверно, что частость события m/n− величина случайная будет

мало отличаться от p, т.е. практически перестает быть случайной величиной.

Теорема Пуассона (следствие из теоремы Бернулли). Если вероятность pi íà- ступления события A в i−м испытании (i = 1, 2, . . . , n) не меняется, когда становятся

известными исходы предыдущих испытаний, а число испытаний n достаточно велико, то вероятность того, что частость события A будет как угодно мало отличаться от средней арифмитической вероятностей pi, сколь угодно близка к единице.

P	( n −				1 + 2	n	n		< ε) ≥ 1 − δ.	(10)
		m p			p	+ . . . + p

Если случайные величины не распределены нормально, то можно наложить на них некоторые весьма не жесткие ограничения и их сумма будет все-таки распределена нормально.

5.4. Центральная предельная теорема

Рассмотренный выше закон больших чисел устанавливает факт приближения средней большого числа случайных величин к определенным постоянным. Но этим не ограни- чиваются закономерности, возникающие в результате суммарного действия случайных величин. Оказывается, что при некоторых условиях совокупное действие случайных ве-

личин приводит к определенному, а именно - к нормальному закону распределения. Центральная предельная теорема представляет собой группу теорем, посвящен-

ных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

43

Теорема Ляпунова. Если независимые случайные величины X1, X2, . . . , Xn имеют

конечные математические ожидания M(Xi) = ai и конечные дисперсии D(Xi) = σ2			,
		i
число их достаточно велико, а при неограниченном возрастании n
lim	m1 + m2 + . . . + mn	= 0,
n→∞ (σ12 + σ22 + . . . + σn2)3=2

то сумма этих случайных величин X1, X2, . . . Xn является нормально распределенной

случайной величиной	∞
	mi = ∫−∞(Xi − ai)3φ(x)dx.	(11)
Дисперсию называют центральным моментом 2-го порядка
	∞
	D(Xi) = ∫−∞(Xi − ai)2φ(x)dx.	(12)

Контрольные вопросы.

1)Неравенство Маркова.

2)Неравенство Чебышева.

3)Теорема Чебышева и ее следствия.

4)Центральная предельная теорема.

44

ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ. 1. Введение.

Первая работа по теории графов, принадлежащая Л. Эйлеру появилась в 1736г. в публикациях Петербурской Академии наук. Л.Эйлер является одной из колоритнейших фигур в истории науки. В 1727 г, когда ему испольнилось 20 лет, он был приглашен в Российскую Академию наук. Много сделал открытий в теологии, медицине, физике, астрономии, математике. Эйлер начал свою работу о графах с рассмотрения одной головоломки "задачи о кенингсбергских мостах".

!

A D

B

Вопрос: можно ли совершить прогулку таким образом, чтобы выйдя из дома, вернуться обратно, пройдя по каждому мосту в точности один раз?

В начале теория графов казалась довольно незначительным разделом математики, т.к. она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и, особенно, ее приложений дало сильнейший толчок развитию теории графов. В настоящее время теория графов находит применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении задач о потоках в сети нефтепроводов, при решении ТЗ и т.п.

Теория графов теперь применяется и таких областях, как экономика, психология и биология.

2. Основные определения.

Определение. Если на плоскости задать конечное множество V точек и конечный набор линий X, соединяющих некоторые пары из точек V , то полученная совокупность точек и линий будет называться графом.При этом элементы множества V называются вершинами графа, а элементы множества X ребрами.

Граф будем обозначать G = V, X .

Определение. Если порядок вершин несущественен, то говорят, что ребро неориентировано, в противном случае ориентировано.

Определение. Граф называется неориентированным, если все его ребра неориентированы, и ориентированным в противном случае.

Графу соответствует геометрическая конфигурация. Вершины обозначаются точками

(кружочками), а ребра - линиями, соединяющими соответствующие вершины.

Определение. Граф называется смешанным, если в нем имеются как ориентированные, так и неориентированные ребра.

45

В дальнейшем, ориентированное ребро называем дугой и обозначаем в круглых скобках, ребро в квадратных скобках.

Пусть x = (a, b)−дуга, тогда вершина a−начальная, вершина b− конечная.

Определение. Вершины v è w называются смежными, если существует ребро(дуга),

соединяющая их.

Определение. Если начальная и конечная вершины совпадают, то ребро называется

петлей.

Определение. Два ребра (дуги) называются смежными, если они имеют общую вершину.

В множестве X могут встречаться одинаковые пары, они называются кратными (или параллельными) ребрами. Количество одинаковых пар (v, w) â X называется кратностью ребра (v, w).

Множество V и набор X определяют граф с кратными ребрами псевдограф. Псев-

дограф без петель называется мультиграфом.

Если в наборе X ни одна пара не встречается более одного раза, то мультиграф назы-

вается простым графом.

Вообще при изображении графов имеется большая свобода в размещении вершин и в выборе формы соединяющих ребер (дуг).

Определение. Будем говорить, что два графа G1 è G2 изоморфны , если между их вершинами можно установить такое взаимно однозначное соответствие, что пары вершин графа G1 в том и только в том случае соединены ребром, когда соединены ребром соответствующие пары вершин графа G2. В случае ориентированных графов это соответствие должно сохранять ориентацию дуг.

термин "изоморфный"→ два слова "изе равный, одинаковый; "морфе вид, форма. Задача. Обозначить вершины второго графа так, чтобы их изоморфность стала оче-

видной.

	7					6
6		1			1	41
5			2	3		2

4	3	5	7

Определение. Степенью вершины графа называется число ребер, которым эта вер-

шина принадлежит.

Определение. Вершина называется изолированной, если если ее степень равна нулю. Определение. Вершина называется висячей, если ее степень равна единице . Определение. Граф, состоящий из изолированных вершин называется нуль графом

èобозначается G0.

показать.

46

Определение. Граф, любые две вершины которого соединены ребром называется пол-

ным и обозначается Kn.

Полный граф, у которого n вершин, имеет 1n(n − 1) ребер. показать, например, на четырехугольнике. 2

Определение. Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересечения ребер являются вершинами графа G.

показать.

Задача о трех колодцах.

Определение. Маршрутом (путем) для графа G(V, X) называется последователь-

ность v1x1v2x2v3 . . . xkvk+1.

Маршрут называется замкнутым, если его начальная и конечная точки совпадают.

Определение. Число ребер (дуг) маршрута (пути) графа называется длиной марш-

ðóòà (ïóòè).

Определение. Незамкнутый маршрут (путь) называется цепью. Цепь, в которой

все вершины попарно различны, называется простой цепью.

Определение. Замкнутый маршрут (путь) называется циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.

1

2

7

	6
	5
3	4

3. Матричные способы задания графов.

Пусть G = V, X ориентированный граф, где V = v1, . . . , vn, X = x1, . . . , xm.

Определение. Матрицей смежности ориентированного графа G называется квадратичная матрица A(G) = [aij] порядка n, у которой

aij =	1 åñëè (vi, vj) X,
{	0 åñëè (vi, vj) / X.

Определение. Если вершина v является концом ребра x, то говорят, что v è x -

инциндентны.

Определение. Матрицей инциндентности ориентированного графа G называется матрица размерности n × m B(G) = [bij], у которой

{ 1, åñëè äóãà xj исходит vi, bij = −1 åñëè äóãà xj заходит vi,

0 в противном случае.

Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.

Составим матрицу смежности:

47

	(1)
1
(3)	2
	(4)
	(2)
	3

	v2	1	0	1	Ò.å.A(G) =	1	0	1	.
		v1	v2	v3		0	1	0
	v1	0	1	0
						1	0	0
	v3	1	0	0

Матрица инциндентности:

v2	-1	1	0	1	Ò.å.B(G) = −1	1	0	1	.
	x1	x2	x3	x4	1	0	−1 −1
v1	1	0	-1	-1
					0	−1 1		0
v3	0	-1	1	0

Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij = k,

где k - кратность дуги (ребра). С помощью матриц смежности и инциндентности всегда можно полностью определить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.

4. Достижимость и связность.

Определение. Вершина w графа G (или ориентированного графа G) называется достижимое из вершины v, åñëè ëèáî w = v, либо существует маршрут из v â w(ïóòü,

соединяющий v è w).

Определение. Граф (ориентированный граф) называется связным, если для любых двух его вершин существует маршрут (путь), который их связывает. Ориентированный граф называется односторонне связным, если если для любых двух его вершин по крайней мере одна достижима из другой.

Определение. Псевдографом D(V, X), ассоциированным с ориентированным псевдографом, называется псевдограф G(V, X0) в котором X0 получается из X заменой всех упорядоченных пар (v, w) на неупорядоченные пары (v, w).

показать.

Определение. Ориентированный граф называется слабо связным, если связным является ассоциированный с ним псевдограф.

5. Эйлеровы и гамильтоновы графы.

Определение. Цепь (цикл) в псевдографе G называется эйлеровым, если она(он) проходит по одному разу через каждое ребро псевдографа G.

Теорема. Для того, чтобы связный псевдограф G обладал эйлеровым циклом, необ-

ходимо и достаточно, чтобы степени его вершин были четными.

Теорема. Для того, чтобы связный псевдограф G обладал эйлеровой цепью, необхо-

димо и достаточно, чтобы он имел ровно две вершины нечетной степени. Определение. Цикл (цепь) в псевдографе G называется гамильтоновым, если он

проходит через каждую вершину псевдографа G ровно один раз.

48

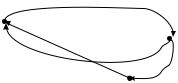
Пример.

1) в графе нет ни эйлерова, ни гамильтонова цикла;				2) в графе есть и эйлеров и
гамильтонов циклы.

3) в графе есть и эйлеров цикл, но нет гамильтонова; 4) в графе есть гамильтонов цикл, но нет эйлерова цикла.

Ãðàô G называется полным, если если каждая его вершина смежна со всеми осталь-

ными вершинами. В полном графе всегда существуют гамильтоновы циклы. Также необходимым условием существования гамильтонова цикла является связность графа.

6. Деревья и циклы.

Определение. Ãðàô G называется деревом, если он является связным и не имеет циклов. Граф G, все компоненты связности которого являются деревьями, называется

лесом.

У графа, который является деревом, число ребер на единицу меньше числа вершин. Дерево не содержит циклов, любые две его вершины можно соеденить единственной простой цепью.

Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдется

висячая вершина, т.к. в противном случае в графе будет цикл. Для графов, которые сами

по себе не являются деревьями, вводится понятие остовного дерева.

Определение. Ãðàô G′ = V ′, X′ называется подграфом графа G = V, X , åñëè

V ′ V è X′ = X ∩ (V ′ × V ′).

Пример.

Определение. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

49

2	2
1	1
3	3

G	4	G’

Пример.

Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) −1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из графа G ровно m(G) − (n(G) − 1) = m(G) − n(G) + 1 ребер.

Определение. Число v(G) = m(G) − n(G)+1 называется цикломатическим числом связного графа G.

Одной из самых распространенных задач является задача построения остовного дерева минимальной длины графа. Для решения этой задачи применяется следующий алгоритм.

1) Выберем в графе G ребро минимальной длины. Вместе с инциндентными ему вершинами оно образует подграф G2.

2)Строим граф G3, добавляя к графу G2 новое ребро минимальной длины, выбранное среди ребер графа G, каждое из которых инциндентно какой либо вершине графа G2, è одновременно инциндентно какой - либо вершине графа G, не содержащейся в графе G2.

3)Строим графы G4, G5, . . . , Gn, повторяя действия пункта 2 до тех пор, пока не переберем все вершины графа G.

Определение. Граф называется нагруженным, если на множестве его дуг задана некоторая функция, которая называется весовой функцией, и определяет длину дуги.

Пример. Определить минимальное остовное дерево нагруженного графа.

	2	(2)	3
		5	(4)
		(1)
	(1)		(3)
		(5)	(3)
	1	(4)	4

В нашем примере - весовая функция определяет длины дуг числами 1, 2, 3, 4, 5.

50