ДМ_МУ_практ(1 часть)

Розв’язок.

Знайдемо двійкове число, що відповідає десятковому числу 14.

Запишемо це	десяткове	число як	суму степенів числа 2, тобто
14 8 4 2 1 23	1 22 1 21	0 20 1110	2	.
10

Таким чином, f14 (x, y) відповідає двійковому числу 11102 .

Побудуємо таблицю істинності, для цього запишемо отримане число в стовпці значення функції таким чином, щоб молодший розряд був у нижньому рядку.

Таблиця 4.2 Таблиця істинності функції f14 (x, y)

	x		y		f14 (x, y)
	0		0		1
	0		1		1
	1		0		1
	1		1		0
Завдання			5.	Чи еквівалентні формули U і B , якщо B x ~ z , а

U (x ~ y) ((y x) z) ?

Розв’язок.

Побудуємо таблиці істинності для формули U (табл. 4.1) і формули B (табл. 4.3). Перевіримо еквівалентність формул за допомогою цих таблиць

(табл. 4.3).

Таблиця 4.3 Узагальнена таблиця істинності функцій, які реалізовані формулами U і B

x	y	z	B	U
0	0	0	1	1
0	0	1	0	1
0	1	0	1	0
0	1	1	0	1
1	0	0	0	0
1	0	1	1	0
1	1	0	0	1
1	1	1	1	1

Аналіз показав, що таблиці істинності функцій не збігаються (стовпці U і B різні), отже, формули нееквівалентні.

Завдання 6. Перевірити, чи справедливі наступні відношення:

а) x ( y ~ z) (x y) ~ (x z) ; б) x( y ~ z) (xy) ~ (xz) .

31

Розв’язок.

а) за допомогою еквівалентних перетворень перетворимо праву і ліву частину відношення x ( y ~ z) x yz yz . Спочатку перетворимо ліву частину: x ( y ~ z) (x y) ~ (x z) (x y)(x z) (x y)(x z)

x xz xy yz x yxz x yz x yz x yz yz .

Ліва і права частина відношення виявилися рівними, отже, відношення справедливе.

б) перетворимо ліву частину відношення:

x( y ~ z) x( yz yz) xyz x yz x( yz yz) .

Перетворимо праву частину відношення:

(x y) ~ (x z) x y x z x y x z x yz (x y)(x z) x y z x x z x y y zx y z x y z x y z y z .

	Результатом перетворення																						є	x( yz yz) x ( yz yz) .																	Це можна
перевірити							за			допомогою										таблиці				істинності								(табл. 4.4),									позначивши
A x( yz y z) , C x ( yz y z) .
	Таблиця 4.4 Таблиця істинності функцій A і C
				y									yz																		A x( yz y z)								C		x	( yz	y		z	)
	x								z							y z							yz yz
	0			0					0		0				1									1								0									1
	0			0					1		0				1									0								0									1
	0			1					0		0				0									0								0									1
	0			1					1		1				0									1								0									1
	1			0					0		0				1									1								1									1
	1			0					1		0				1									0								0									0
	1			1					0		0				1									0								0									0
	1			1					1		1				1									1								1									1
	Стовпці A і C не є рівними, отже, відношення несправедливе.
	Завдання 7. Знайти функцію, двоїсту функції																															f (x, y, z) , якщо відомо, що

f (x, y, z) 1 тільки на інтерпретаціях (001), (011), (111).

Розв’язок.

Побудуємо таблицю істинності функції f (x, y, z) (табл. 4.5). Для стовпця значень функції f (x, y, z) генеруємо набір протилежних (інверсних) значень (10101110). Записавши цей набір у зворотній послідовності, отримаємо, таким чином, стовпець значень двоїстої функції f * .

32

Таблиця 4.5 Таблиця істинності двоїстих функцій

x	y	z	f (x, y, z)	f * (x, y, z)
0	0	0	0	0
0	0	1	1	1
0	1	0	0	1
0	1	1	1	1
1	0	0	0	0
1	0	1	0	1
1	1	0	0	0
1	1	1	1	1

Завдання 8. Знайти булеву функцію, яка є двоїстою булевій функції f x ( y z (u v)).

Розв’язок.

Використовуючи правило знаходження двоїстих формул булевої алгебри (принцип двоїстості), тобто замінивши всі кон’юнкції на диз’юнкції, всі диз’юнкції на кон’юнкції, поставивши дужки, де необхідно, щоб порядок виконання операцій залишився таким, як був, знаходимо двоїсту булеву функцію f * x ( y z (u v))* x y (z u v) .

Завдання 9.			Булеві функції		f (x, y, z) і g(x, y, z)			задаються таблицями
істинності (табл. 4.6). Визначити, чи є дані булеві функції самодвоїстими.
Таблиця 4.6 – Таблиця істинності функцій f (x, y, z)								і g(x, y, z)
	x		y	z		f (x, y, z)		g(x, y, z)
	0		0	0		0		0
	0		0	1		1		1
	0		1	0		1		0
	0		1	1		1		1
	1		0	0		0		1
	1		0	1		0		1
	1		1	0		0		0
	1		1	1		1		0

Розв’язок.

З таблиці 4.6 видно, що кожне значення булевої функції f (x, y, z) є запереченням симетричного йому значення, наприклад: булева функція на

33

інтерпретації (0,0,0) дорівнює нулю, тобто f (0, 0,0) 0 , симетричне значення цієї функції на інтерпретації (1, 1, 1) дорівнює одиниці, тобто f (1,1,1) 1.

Отже, функція f (x, y, z) є самодвоїстою.

Для булевої функції g(x, y, z) є такі значення функції, які не є рівними запереченню симетричних їм значень, наприклад: булева функція на інтерпретації (0,0,0) дорівнює нулю, тобто g(0,0,0) 0 , а симетричне значення цієї функції на інтерпретації (1, 1, 1) теж дорівнює нулю, тобто g(1, 1, 1) 0 .

Отже, функція g(x, y, z) не є самодвоїстою.

5 НОРМАЛЬНІ ФОРМИ ЗОБРАЖЕННЯ БУЛЕВИХ ФУНКЦІЙ

5.1 Мета заняття

Ознайомлення на практичних прикладах з поняттям «нормальна форма» булевої функції. Вивчення способів зображення формул у вигляді диз’юнктивних і кон’юнктивних нормальних форм (ДНФ і КНФ). Вивчення алгоритмів переходу від таблиць істинності булевих функцій і від довільних формул до досконалої диз’юнктивної і досконалої кон’юнктивної нормальних форм (ДДНФ і ДКНФ).

5.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: основні поняття і визначення, які пов’язані з «нормальною формою» булевої функції; ДДНФ і ДКНФ булевої функції; теореми про диз’юнктивне і кон’юнктивне розкладання булевої функції за змінними; правила переходу від таблиць істинності булевої функції до ДДНФ і ДКНФ булевої функції; правила переходу від довільних формул булевої функції до ДДНФ і ДКНФ.

Підготовка і виконання практичного заняття проводиться у два етапи. Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень: елементарна кон’юнкція; елементарна диз’юнкція; ДНФ; конституента одиниці (мінтерм n -го рангу); ДДНФ; КНФ; конституента нуля (макстерм n -го рангу); ДКНФ.

Під час виконання першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих

34

вище понять і визначень. Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, які представлено у підрозділі 5.3, на основі запропонованих типових прикладів (див. підрозділ 5.4).

5.3 Контрольні запитання і завдання 5.3.1 Контрольні запитання

1.На прикладі булевих функцій опишіть поняття «нормальна форма»

функції.

2.Що являє собою елементарна кон’юнкція, елементарна диз’юнкція?

3.Яка формула називається диз’юнктивною нормальною формою, кон’юнктивною нормальною формою булевої функції?

4.Дайте визначення поняттям мінтерм, макстерм, конституента одиниці, конституента нуля.

5.Що таке досконала нормальна форма і які властивості в неї є?

6.Скільки є різних конституент одиниці та нуля для функції n змінних f (x1 , x2 , ..., xn ) ?

7.Скільки ДНФ і скільки СДНФ може мати булева функція?

8.Запишіть формули диз’юнктивного розкладання булевих функцій від n змінних за k (k n) змінними, за всіма n змінними, за однією змінною.

9.Запишіть формули кон’юнктивного розкладання булевих функцій від n змінних за k (k n) змінними, за всіма n змінними, за однією змінною.

10.Опишіть алгоритми переходу від таблиці істинності булевої функції до ДДНФ і ДКНФ.

11.Сформулюйте правила перетворення довільної формули алгебри логіки в нормальну форму з використанням законів булевої алгебри.

5.3.2 Контрольні завдання

Завдання 1. Знайти диз’юнктивне розкладання наступних булевих функцій за змінними x, z :

а) (x (z yz))(z xz y) ;

б) ((x y)(y z) (z x)) (x z) ;

в) (x z)(xt yt xt yt)(x z) .

35

Завдання 2. Знайти кон’юнктивне розкладання наступних булевих функцій за змінними x, z :

а) (x z y)(x y x y z)(x y) ;

б) ((y z)(t yz)) t x ((z y)(t z);

в) yt ((z t)(x z)(t z)(x z)) yt .

Завдання 3. Записати диз’юнктивне розкладання булевої функції f (x, y, z, t) (x y z) (t x) за змінною x .

Завдання 4. Записати конституенти нуля та одиниці булевої функції, що відповідають інтерпретаціям функції чотирьох змінних.

Завдання 5. За допомогою еквівалентних перетворень привести до ДНФ

наступні формули: а) F (x yz)(x z) ; б) F (x y) (xy z) .
Завдання 6. Представити у вигляді ДДНФ і ДКНФ наступні функції:
а) f	(10001110) , де f			стовпець	значень функції з таблиці
істинності;	б)	f (01100110);		в)	f (x, y, z) (x y) z ;	г)

f (x, y) (x y)(x y) ; д) f (x, y, z, t) ((x y) z) t ; е) f201(x, y, z) .

Завдання 7. Скласти алгоритм переходу від таблиці істинності булевої

функції до ДДНФ даної функції.
Завдання 8. За допомогою перетворень виду A Ax Ax,	A A A

перейти від заданої ДНФ f (x1, x2 , x3 ) x1 x2 x1x3 до ДДНФ.

Завдання 9. Записати ДДНФ для функції f (x1 , x2 , x3 ) , що має нульові значення на всіх непарних двійкових наборах.

Завдання 10. Записати ДКНФ для функції від 4-х змінних, яка має одиничні значення на нульовому наборі та всіх парних двійкових наборах.

Завдання 11. Нехай функція f (x, y, z)				задана таким чином: f (x, y, z) 0 ,
якщо y 1 або y z , а інакше		f (x, y, z) 1. За допомогою таблиці істинності
функції записати множину Q	f	таку, що Q	f	{ | R3 и f ( ) 0} і записати

ДКНФ і ДДНФ даної функції.

5.4 Приклади аудиторних і домашніх завдань

Завдання 1. Записати диз’юнктивне розкладання функції

f (x, y, z, t) (x y z) t за змінними x, z .

36

Розв’язок.

Скористаємося теоремою про розкладання булевих функцій за k

змінними:	f (x, y, z, t) x 1 z 2 f ( 1 ,		y, 2 , t) x0 z0	f (0, y, 0, t)
	1 , 2
x0 z1 f (0, y, 1, t) x1 z0 f (1, y, 0,		t) x1	z1 f (1, y, 1,	t)

x z f (0, y, 0, t) x z f (0, y, 1, t) x z f (1, y, 0, t) x z f (1, y, 1, t) .

Обчислимо:

f (0, y, 0, t) (0 y 0) t 0;

f (0, y,1, t) (0 y 1) t t ;

f (1, y, 0, t) (1 y 0) t 0 ;

f (1, y,1, t) (1 y 1) t y t .

Підставимо значення f (0, y, 0, t) , f (0, y,1, t) , f (1, y, 0, t) , f (1, y,1, t) у формулу диз’юнктивного розкладання за змінним x, z :

f (x, y, z,t) x z 0 x z t x z 0 x z ( y t) x z t x z y t.

Завдання 2. Записати кон’юнктивне розкладання функції f (x, y, z) xy z за змінною x .

Розв’язок.

Скористаємося теоремою про кон’юнктивне розкладання булевої функції (за однією змінною):

f (x, y, z) (x0 f (0, y, z)) (x1 f (1, y, z)) (x f (0, y, z)) (x f (1, y, z))

(x 0 y z)(x 1 y z) (x z)(x y z) .

Завдання 3. Представити у вигляді досконалої дизюнктивної нормальної форми і досконалої кон’юнктивної нормальної форми функцію

f (x, y, z) (x y) yz .

Розв’язок.

Побудуємо таблицю істинності даної функції (табл. 5.4).

37

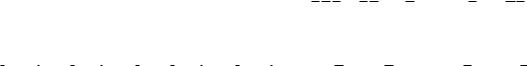
Таблиця 5.4 – Таблиця істинності функції f (x, y, z) (x y) yz

			(x y)
x	y	z			y z		yz yz
0	0	0	0		0		1
0	0	1	0		0		1
0	1	0	1		0		0
0	1	1	1		1		1
1	0	0	1		0		0
1	0	1	1		0		0
1	1	0	0		0		1
1	1	1	0		1		1

ДДНФ ( fСДНФ ) побудуємо на одиничних значеннях функції:

fСДНФ x0 y0 z0 x0 y0 z1 x0 y1 z1 x1 y1 z0 x1 y1 z1 x yz x yz xyz xyz x yz .

ДКНФ ( fСКНФ ) побудуємо на нульових значеннях функції:

fСКНФ (x0 y1 z0 )(x1 y0 z0 )(x1 y0 z1 ) (x y z)(x y z)(x y z) .

Завдання 4.

Записати конституенти нуля та одиниці, що відповідають інтерпретаціям булевої функції трьох змінних.

Розв’язок.

Конституента нуля і конституента одиниці булевої функції однозначно визначаються номерами відповідних їм інтерпретацій. Конституента нуля функції f (x, y, z) являє собою елементарну диз’юнкцію. Інтерпретація, що обертає в нуль дану елементарну диз’юнкцію, перетворює в нуль і функцію f (x, y, z) . Конституента одиниці функції f (x, y, z) являє собою елементарну кон’юнкцію. Інтерпретація, що обертає в одиницю дану елементарну кон’юнкцію, перетворює в одиницю і функцію f (x, y, z) .

Конституенти нуля і конституенти одиниці для функцій трьох змінних наведені в табл. 5.4.

38

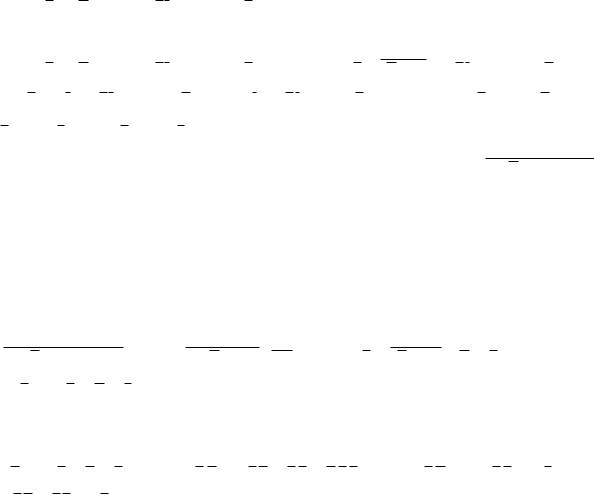
Таблиця 5.4 – Конституенти нуля і конституенти одиниці для функцій

трьох змінних			f (x, y, z)
	Номер			Інтерпретація				Конституента								Конституента
	інтерпре-				y
			x				z	одиниці										нуля
	таціїи
	0		0		0		0										x y z
									x y z
	1		0		0		1		x yz								x y z
	2		0		1		0		xy z								x y z
	3		0		1		1			xyz							x y z
	4		1		0		0		x y z								x y z
	5		1		0		1		x yz								x y z
	6		1		1		0		xy z								x y z
										xyz
	7		1		1		1										x y z

Завдання 5.

За допомогою еквівалентних перетворень привести до ДНФ формулу

F ((x yzt)((y t) xzt) yz) (x t) .

Розв’язок.

F((x yzt)((y t) xzt) yz) (x t) ((x yzt)(( y t) xzt) yz) (x t)

((x yzt)(yt xzt) yz) x t xyt xzt yz x t t xy xz yz x

t x y z yz x y z t .

Завдання 6. Побудувати ДДНФ функції f (x, y, z) xy (x( y z) yz) , використовуючи правила перетворення довільної формули алгебри логіки до ДДНФ.

Розв’язок.

Скористаємося правилами перетворення довільної формули алгебри логіки до ДДНФ.

Опускаємо заперечення на змінні, використовуючи закон де Моргана: x y (x ( y z) y z) x y (x ( y z)) ( y z) xy (x ( y z)) ( y z)

xy (x ( yz))(y z).

Побудуємо диз’юнктивну нормальну форму, використовуючи дистрибутивний закон, закони ідемпотентності й протиріччя:

x y (x ( y z))(y z) x y (x y y z y x z y z z) x y x y 0 x z y z

xy x y xz yz .

39

Булева функція залежить від трьох змінних, тому в елементарні кон’юнкції необхідно ввести відсутні змінні, використовуючи закон виключеного третього:

x y x y x z y z x y (z z) x y(z z) x ( y y) z (x x) y z .

Використовуючи дистрибутивний закон, розкриємо дужки і зведемо подібні для одержання ДДНФ:

xyz xyz x yz x yz xyz x yz xyz xyz xyz xyz x yz x yz xyz .

Одержана досконала диз’юнктивна нормальна форма заданої булевої функції: f (x, y, z) xyz xy z x yz x yz xyz .

Завдання 7. Скласти алгоритм переходу від таблиці істинності булевої функції до ДКНФ.

Розв’язок.

Для переходу від таблиці істинності булевої функції до ДКНФ можна скористатися наступним алгоритмом:

а) виділити в таблиці істинності булевої функції всі інтерпретації, на яких значення функції дорівнює нулю;

б) записати конституенти нуля, що відповідають відзначеним інтерпретаціям;

в) одержати ДКНФ функції за допомогою з’єднання операцією кон’юнкції записаних конституент нуля.

6 МІНІМІЗАЦІЯ БУЛЕВИХ ФУНКЦІЙ

6.1 Мета заняття

Ознайомлення c цілями мінімізації булевих функцій і способами визначення складності їх диз’юнктивних і кон’юнктивних нормальних форм. Вивчення методу мінімізуючих карт (діаграм Карно-Вейча).

6.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: основні поняття і визначення, які використовуються при мінімізації булевих функцій; оцінка форми булевої функції за допомогою індексу (коефіцієнта) простоти; задача мінімізації булевих функцій в аналітичній і геометричній формі (задача про

40