Эконометрика. Учебное пособие

ры, влияющие на Y, которые не учтены в модели. Влияние этих факторов приводит к тому, что наблюдаемые точки лежат вне прямой yi xi . Возмож-

но, что существуют также другие факторы, которые оказывают такое слабое влияние, что их не стоит учитывать. Кроме того, могут быть факторы, которые являются существенными, но почему-то таковыми не считаются. Если точно знать, какие переменные должны присутствовать в модели и иметь возможность точно их измерить, то можно было бы включить их в уравнение. Проблема состоит в том, что мы не можем быть априори уверены в том, что какие-то факторы влияют на y, а какие-то нет. Проблема включения или невключения новых регрессоров в модель будет рассмотрена нами позже, при изучении множественной регрессии.

2. Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Например, можно пытаться строить модель линейной связи, хотя на самом деле переменные зависят друг от друга по другому закону (показательному, логарифмическому или степенному). Данная проблема будет изучена при рассмотрении нелинейной регрессионной модели.

3. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить вклад в случайный член.

Остаточный член является суммарным проявлением всех этих факторов. Иногда остаточный член называют шумом.

2.3. Регрессия по методу наименьших квадратов

Пусть из некоторой генеральной совокупности получена выборка

	X	x1	x2	…		xn
Эмпирическое уравнение	Y	y1	y2	…	yn
	линейной регрессии – уравнение вида
y*(x) a bx,						(2.1)

где a и b – оценки параметров и , полученные в результате оценивания модели по данной выборке, y*(x) будем называть прогнозным значением величины Y при заданном значении X. Эмпирическое уравнение может быть записано для каждого наблюдения

yi* yi*(x) a bxi , i 1,2, ,n.

Остаток в i-ом наблюдении – разность между i-ым наблюдаемым значением величины Y и ее прогнозным значением

ei yi yi*.

За исключением случайного совпадения, остаток в наблюдении будет отличен от нуля. Очевидно, что чем меньше величина остатков, тем лучше полученные оценки a и b. Минимизировать остатки можно различными способа-

21

ми, но наиболее общеупотребительным и хорошо разработанным является метод, основанный на минимизации суммы квадратов остатков:

n

Se12 e22 ... en2 ei2 ; i 1

n

S(a,b) yi a bxi 2 .

i 1

Величина S(a,b) будет зависеть от выбора a и b, так как они определяют положение прямой. В соответствии с этим критерием, чем меньше S, тем строже соответствие. Если S 0, то получено абсолютно точное соответствие, так как это означает, что все остатки равны нулю. В этом случае линия регрессии будет проходить через все точки, однако, это невозможно из-за наличия случайного члена.

Метод наименьших квадратов (МНК) – метод нахождения оценок па-

раметров регрессии, основанный на минимизации суммы квадратов остатков всех наблюдений. При выполнении определенных условий метод наименьших квадратов дает «наилучшие» оценки для и (точные формулировки относительно условий получения «наилучших» оценок будут даны позднее при изучении множественной регрессии).

Заметим, что данное выражение S(a,b) является квадратичной функцией от a и b. Если предположить, что значения (xi,yi ) зафиксированы, то влиять на величину S можно, изменяя значения a и b. Для того чтобы величина S(a,b) была минимальной, необходимо, чтобы частные производные равнялись нулю, то есть

		S		n
				2 (yi (a bxi )) 0,
		a
				i 1
	S			n
			2 (yi (a bxi ))xi		0.
	b			i 1

Эти уравнения известны как нормальные уравнения для коэффициен-

тов регрессии. Используя обозначение для средних значений, эти уравнения можно переписать в виде:

a bx y ,

ax b1n xi2 1n xi yi.

Решая полученные уравнения относительно a и b, находим

		1	xi yi					x				y
b	n												,	(2.2)
			1	xi2
									x		2
			n							.
			a		y	bx								(2.3)
			22

Учитывая формулы (1.3)–(1.5), можно записать

b	Cov(x,y)	r	Sy		.	(2.4)
	D		S
		xy		x
	x

При таких значениях a и b график уравнения (2.1) проходит через точку

x,y , которая называется центром рассеивания.

При интерпретации уравнения линейной регрессии чрезвычайно важно помнить о следующем: во-первых, a является лишь оценкой , а b – оценкой. Поэтому вся интерпретация в действительности представляет собой лишь оценку; во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей.

”Наилучшая” по методу наименьших квадратов прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y f (x) является, например, квадратичной, то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется наилучшая. Если величины x и y вообще не связаны, то всегда сможем найти наилучшую линейную функцию для данной выборки. Но эта линейная зависимость не будет отражать взаимосвязь между переменными (b будет близко к нулю).

Пример 4. Для выборки из примера 1 найти эмпирическое уравнение линейной регрессии.

Найти уравнение регрессии – это значит найти оценки a и b. Они могут быть найдены с использованием программы Microsoft Excel несколькими способами.

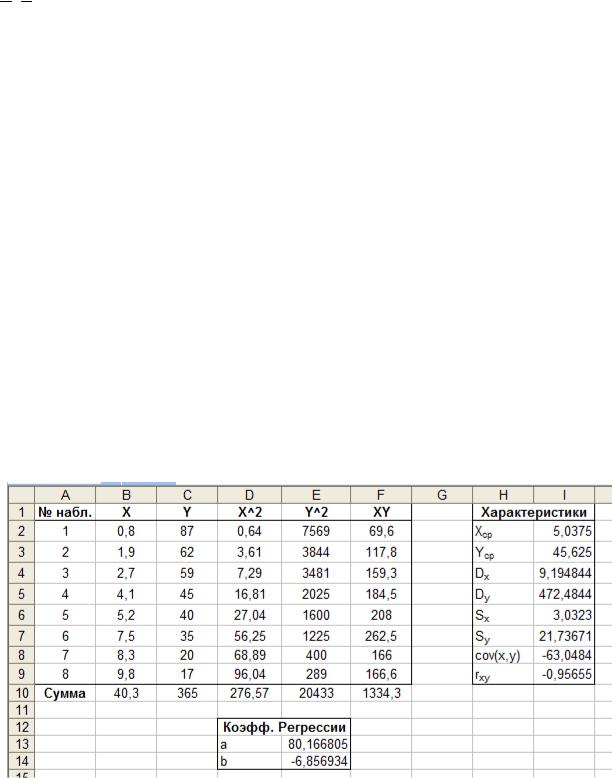
Способ 1. Коэффициенты a и b вычислим непосредственно по формулам (2.3) и (2.4). Соответствующие расчеты представлены на рисунках 2.2 и 2.3.

Рис. 2.2. Вычисление эмпирических коэффициентов регрессии

23

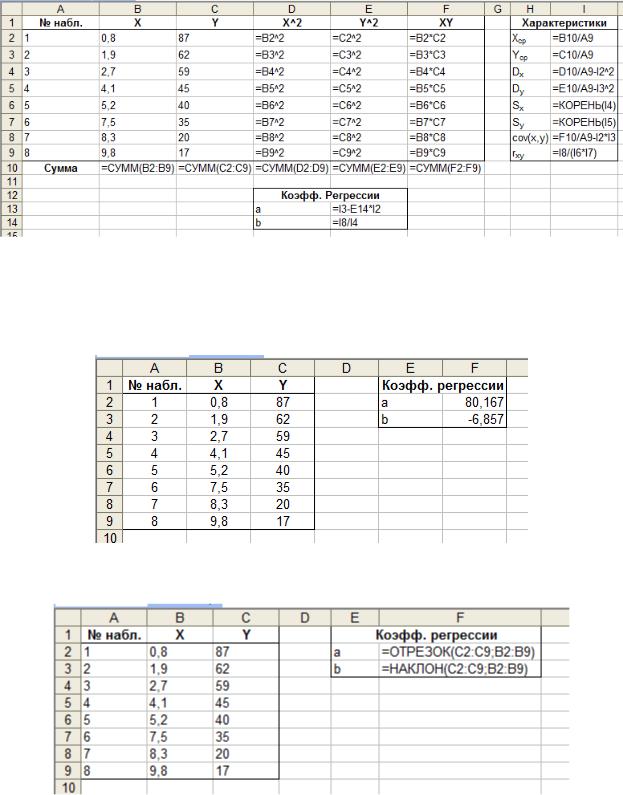
Рис. 2.3. Формулы для вычисления эмпирических коэффициентов регрессии

Способ 2. Воспользуемся встроенными функциями НАКЛОН и ОТРЕЗОК, которые возвращают значения коэффициентов a и b, соответственно. Результаты вычислений и формулы представлены на рисунках 2.4 и 2.5.

Рис. 2.4. Вычисление эмпирических коэффициентов регрессии с помощью встроенных функций

Рис. 2.5. Формулы для вычисления эмпирических коэффициентов регрессии с помощью встроенных функций

Способ 3. Получить эмпирическое уравнение (а также и его график) можно при помощи встроенного инструмента Линия тренда. Для этого нужно построить поле корреляции (см. пример 3), затем правым щелчком мыши по любой точке корреляци-

24

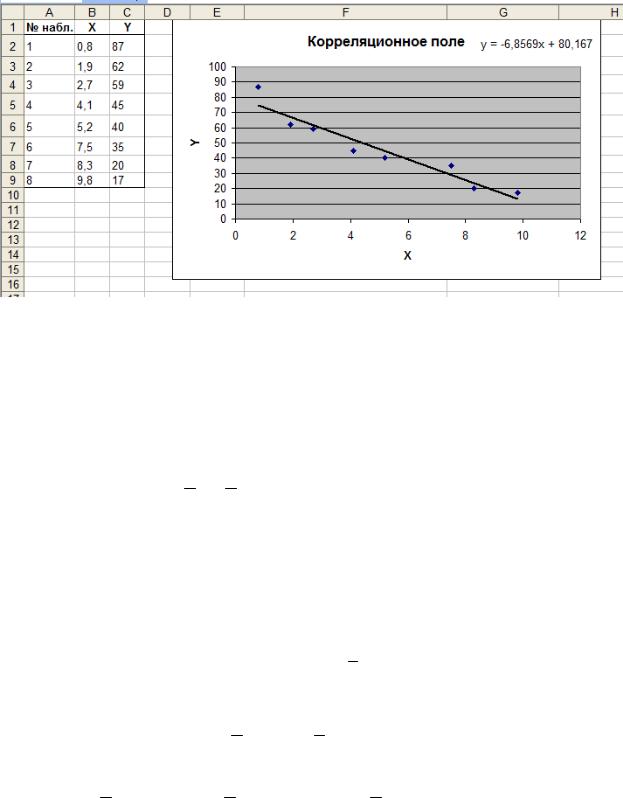
онного поля открыть контекстное меню и выбрать в нем пункт Добавить линию тренда. В появившемся диалоговом окне выбрать Линейный и установить флажок на Показывать уравнение на диаграмме. Полученный результат представлен на рисунке 2.6.

Рис. 2.6. Вычисление эмпирических коэффициентов регрессии с помощью инструмента Линия тренда

2.4. Основное дисперсионное тождество регрессионного анализа

Пусть по выборке x1,y1 , x2,y2 ,..., xn, yn построено эмпириче-

ское уравнение регрессии

						y* y*(x) a bx ,
		cov(x, y)					i	i	i
	где b		,	a	y	bx	, y	– наблюденные значения, y*		– прогнозные
		Dx					i		i

значения.

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Непосредственному расчету F-критерия предшествует анализ дисперсий. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной y от среднего значения y на две части – «объясненную» и «необъясненную». Выполним это разложение. Очевидно, справедливо равенство

yi y yi* y yi yi* .

Возведем обе части этого равенства в квадрат и просуммируем по i:

yi y 2 yi* y 2 2 yi* y yi yi* yi yi* 2 .

25

Можно проверить, что yi yi* yi* y 0 и мы получаем основ-

ное дисперсионное тождество регрессионного анализа

yi y 2 yi* y 2 yi yi* 2 .

Полученное тождество является отправной точкой для проведения анализа качества полученного эмпирического уравнения. Систему понятий, связанную с основным дисперсионным тождеством удобно представить в виде таблицы.

							Таблица 2.1
	yi	y	2	yi*	y	2	yi yi* 2
				Сумма квадратов отклоне-			Остаточная (необъяснен-
	Общая (полная) сумма			ний объясненная регрессией
							ная) сумма квадратов от-
	квадратов отклонений			(объясненная сумма, регрес-
				сионная сумма)			клонений
	Σобщ			Σрег			Σост

Отметим, что данные суммы связаны с дисперсиями переменных следующим образом:

D		общ ,	D	ост ,	D	рег	.
	y	n 1	ост	n 2	x	b2(n 1)

При этом дисперсию Dост называют остаточной или необъясненной.

Общая сумма квадратов отклонений индивидуальных значений результа-

тивного признака y от среднего значения y вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор x и прочие факторы. Если фактор не оказывает влияния на результат,

то линия регрессии на графике параллельна оси Ox, b 0 и y y. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если прочие факторы не влияют на результат, то y связан с x функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.

2.5. Коэффициент детерминации. Критерий Фишера (F-тест)

Коэффициент детерминации R2 – это отношение объясненной суммы квадратов к общей, т.е.

	2		yi*	y	2		рег
	R							.
			yi	y	2		общ
			26

Коэффициент детерминации характеризует долю дисперсии результативного признака, объясняемую регрессией, в общей дисперсии результативного признака. Соответственно, величина

	2		yi	yi* 2				ост
	1 R
			yi		y	2		общ

характеризует долю дисперсии y, вызванную влиянием остальных неучтенных в модели факторов.

Отметим, что коэффициент детерминации R2 связан с коэффициентом корреляции rxyсоотношением

R2 rxy2 .

Коэффициент детерминации может принимать значения от 0 до 1. Равенство R2 0 возможно тогда и только тогда, когда рег 0. Это означает, что

дисперсия результативного признака вызвана исключительно влиянием неучтенных в модели факторов. Другой крайний случай R2 1 означает точную подгонку: все наблюдаемые значения лежат на регрессионной прямой. Чем ближе к 1 значение R2 , тем лучше качество подгонки, y* более точно аппроксимирует наблюдаемые значения yi .

Проверка значимости линейной регрессионной модели сводится к проверке нулевой гипотезы H0 : 0 (модель незначима) при альтернативной ги-

потезе H1 : 0 (модель значима).
Чтобы проверить H0	по выборке x1,y1 , x2,y2				,..., xn, yn	объема
n, необходимо вычислить наблюдаемое значение критерия
F		рег (n 2)		R2(n 2)	.	(2.5)
		ост
набл				1 R2

Если H0 верна, то статистика Fнабл имеет распределение Фишера со сте-

пенями свободы 1 и (n 2). При помощи функции FРАСПОБР по заданному уровню значимости и степеням свободы 1 и (n 2) определяем критическую точку Fкр F ,1,n 2 FРАСПОБР ,1,n 2 . Если Fнабл Fкр с некоторым уровнем значимости (обычно берут 0,05), то нулевая гипотеза отвергается и регрессия считается значимой. В противном случае нет оснований для того чтобы отвергнуть нулевую гипотезу, поэтому полученное уравнение регрессии считается незначимым.

Для парной линейной регрессии гипотеза H0 : 0 равносильна гипоте-

зе H0 : xy 0, процедура проверки которой была описана в пункте 1.4 (следо-

27

вательно, выводы, получаемые при проверке этих гипотез должны совпадать).

То есть значимость линейной регрессионной модели равносильна наличию линейной корреляции между X и Y.

Пример 5. Вычислим коэффициент детерминации эмпирического уравнения регрессии, построенного в примере 4 и проверим значимость регрессии с помощью критерия Фишера при уровне значимости α=0,05.

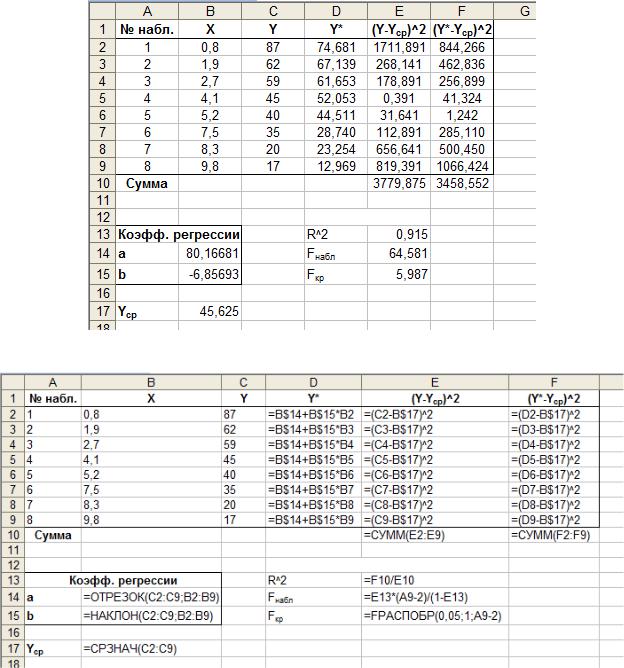
Расчетный лист для вычисления коэффициента детерминации и проверки значимости регрессии представлен на рисунках 2.7 и 2.8.

Рис. 2.7. Проверка значимости модели по критерию Фишера (значения)

Рис. 2.8. Проверка значимости модели по критерию Фишера (формулы)

Подчеркнем, что в ячейках E10 и F10 вычисляются Σобщ и Σрег соответственно.

28

n 2

Поскольку Fнабл=64,581>Fкр=5,987, то коэффициент детерминации статистически значим, а следовательно статистически значимо и уравнение регрессии.

2.6. Интервальные оценки параметров уравнения регрессии

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: mb и ma .

Корень квадратный из необъясненной дисперсии, т.е. величина

						yi yi* 2
S			ост
			n 2			n 2

является оценкой среднего квадратичного отклонения остатков.

Стандартная ошибка оценки b определяется по формуле

S2

mb xi x 2 .

Величина стандартной ошибки совместно с t-распределением Стьюдента при степенях свободы применяется для проверки значимости коэффи-

циента регрессии и для расчета его доверительных интервалов.

Для оценки значимости коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определятся наблюдаемое значение t-

критерия Стьюдента: tb b , которое затем сравнивается с критическим зна-

mb

чением t ,n 2 при определенном уровне значимости α и числе степеней свободы n 2 .

Отметим, что справедливо равенства tb2 Fнабл , где Fнабл – наблюдаемое значение критерия Фишера, вычисляемое по формуле (2.5).

Доверительный интервал для коэффициента регрессии при задан-

ном уровне значимости определяется как

b t( ,n 2) mb .

Это

означает,

что

коэффициент

принадлежит

интервалу

b t( ,n 2) mb;b t( ,n 2) mb

с вероятностью 1 . Например, при

0,05 такой интервал называют 95% доверительным интервалом.

Стандартная ошибка параметра a определяется по формуле:

m

S2

xi2

.

a

n xi

2

x

29

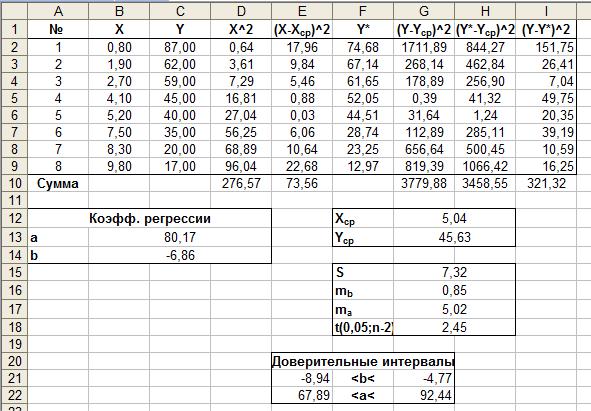
Доверительный интервал для параметра a при заданном уровне значимости определяется по формуле:

a t( ,n 2) ma .

Доверительный интервал для прогнозного значения приближенно задается двумя прямыми

y_(x) y*(x) t( ,n 2)S и y (x) y*(x) t( ,n 2)S .

Пример 6. Найти стандартную ошибку регрессии и 95%-ные доверительные интервалы для коэффициентов регрессии, построенной в примере 4.

Необходимые расчеты представлены на рисунках 2.9 и 2.10.

Рис. 2.9. Расчет доверительных интервалов

30