
- •Определители: определение, вычисление определителей 2-го и 3-го порядка. Решение слау методом Крамера.
- •Прямая на плоскости. Уравнения (вывод)
- •Плоскость. Уравнение (вывод).
- •Прямая в пространстве, уравнения (вывод).
- •Общее уравнение прямой
- •Кривые второго порядка.
- •Числовые последовательности: определение.
- •Непрерывность функции в точке. Точки разрыва, их виды, примеры. Свойства функции, непрерывной на отрезке.
- •Называется точкой разрыва первого рода:
- •Называется точкой разрыва второго рода:
- •Определение производной, её геометрический и физический смысл.
-
Определители: определение, вычисление определителей 2-го и 3-го порядка. Решение слау методом Крамера.
Матрица - это прямоугольная таблица, составленная из чисел, которые нельзя менять местами. Квадратная матрица - таблица, у которой число строк и число столбцов одинаково. Определитель может быть только у квадратной матрицы.
Итак, пусть дана квадратная таблица, состоящая из чисел, расположенных в n строках (горизонтальных рядах) и в n столбцах (вертикальных рядах). С помощью этих чисел по некоторым правилам находят число, которое и называют определителем n-го порядка и обозначают следующим образом:
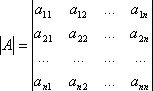
Числа ![]() называют элементами определителя
(первый индекс означает номер строки,
второй – номер столбца). Порядок
определителя – это число его строк и
столбцов.
называют элементами определителя
(первый индекс означает номер строки,
второй – номер столбца). Порядок
определителя – это число его строк и
столбцов.
Определитель второго порядка есть число, получаемое следующим образом:
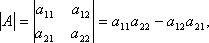
Определитель третьего порядка – это число, получаемое так:
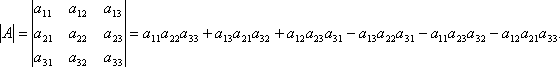
Запомнить эту формулу трудно. Однако существует простое правило, называемое правилом треугольников, которое позволяет легко воспроизвести выражение .
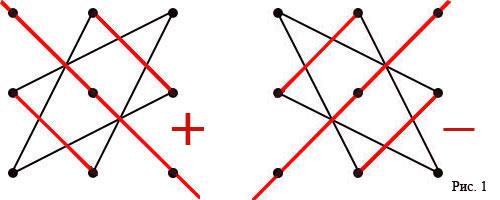
Формула показывает, что со своими знаками берутся произведения элементов главной диагонали, а также элементов, расположенных в вершинах двух треугольников, основания которых ей параллельны; с противоположными – произведения элементов побочной диагонали, а также элементов, расположенных в вершинах двух треугольников, которые ей параллельны.
Метод Крамера применим к СЛАУ, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничение на коэффициент системы. Необходимо, чтобы все уравнение были линейно независимы. Для этого необходимо, чтобы определитель матрицы не был равен 0.
Пример
Система линейных уравнений:

Определители:
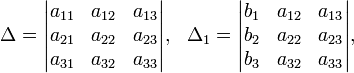
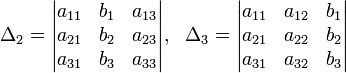
Решение:
![]()
-
Матрицы: определение, виды матриц. Линейные операции над матрицами, примеры. Умножение матриц, примеры. Обратная матрица. Алгебраическое дополнение элемента матрицы, минор элемента матрицы. Условие существования обратной матрицы. Алгоритм нахождения обратной матрицы. Решение СЛУ с помощью обратной матрицы. Ранг матрицы. Теорема Кронекера – Капелли. Решение СЛУ методом Гаусса-Жордано, примеры.
Прямоугольная таблица, состоящая из чисел, расположенных в m строках и n столбцах, называется mn-матрицей (или просто матрицей) и записывается так:

Матрица называется прямоугольной,
если
![]() .
.
Если же m = n , то матрица называется квадратной, а число n – её порядком.
Матрицы называются равными, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают.
Матрица называется нулевой, если всё её элементы равны нулю.
Матрицей-строкой (или строчной) называется 1n-матрица, а матрицей-столбцом (или столбцовой) – m1-матрица.
Произведением матрицы A на произвольное число α называется матрица, элементами которой являются произведения элементов матрицы A на α, т.е.
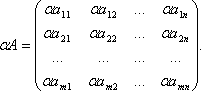
Суммой (разностью) двух mn-матриц A и B называется матрица С , элементы которой равны суммам (разностям) соответствующих элементов матриц A и B , т.е.
![]() для
суммы матриц и
для
суммы матриц и
![]() для
разности матриц (i =
1, 2, ..., m; j =
1, 2, ..., m),
где
для
разности матриц (i =
1, 2, ..., m; j =
1, 2, ..., m),
где
![]() –
элементы матрицы А ,
–
элементы матрицы А ,
![]()
– элементы матрицы В .
Пример . Найти сумму и разность матриц
![]() и
и
![]()
В соответствии с определением находим:
![]() ;
;
![]() .
.
Произведением
mp-матрицы А на pn-матрицу В
справа (или матрицы
В на матрицу А слева)
называется mn-матрица
С, элементы ![]() (i =
1, 2, ..., m; j =
1, 2, ..., n)
которой равны сумме произведений
элементов i-й
строки матрицы А на
соответствующие элементы j-го
столбца матрицы В ,
т.е.
(i =
1, 2, ..., m; j =
1, 2, ..., n)
которой равны сумме произведений
элементов i-й
строки матрицы А на
соответствующие элементы j-го
столбца матрицы В ,
т.е.
![]() (4)
(4)
Произведение матрицы А на матрицу В обозначается АВ . Таким образом, произведение АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .
Пример 5. Найти произведение АВ , если
![]() ,
,
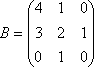 .
.
Решение. Удобно нахождение произведения матриц А и В записывать так, как на рис.2:
На
схеме маленькие стрелки показывают,
элементы какой строки матрицы А на
элементы какого столбца матрицы В нужно
перемножить для получения элементов
матрицы С ,
а пунктиром соединены соответствующие
элементы. В результате получаем:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом,
![]() .
.
Каждая квадратичная матрица с определителем, не равным нулю, имеет обратную матрицу, и притом только одну.
![]() , где
, где
![]() (определитель
не равен нулю),
(определитель
не равен нулю),
![]() -
матрица, присоединённая к матрице А.
-
матрица, присоединённая к матрице А.
Минор
Минором ![]() элемента
элемента ![]() матрицы
n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы
А вычеркиванием
i-й
строки и j-го
столбца.
матрицы
n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы
А вычеркиванием
i-й
строки и j-го
столбца.

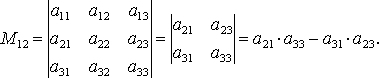
Пример
1. Составить
минор ![]() ,
полученную из исходной матрицы:
,
полученную из исходной матрицы:
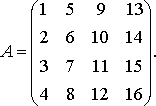
Решение:

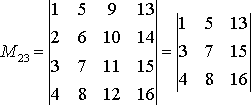 .
.
Алгебраические дополнения
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
![]()
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Пример 1. Найти алгебраические дополнения всех элементов матрицы
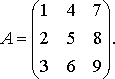
Решение:
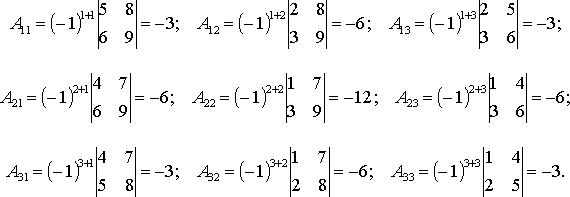
Дана
матрица  .
Найти обратную матрицу.
Р
е ш е н и е: Вычисляем определитель
матрицы A:
.
Найти обратную матрицу.
Р
е ш е н и е: Вычисляем определитель
матрицы A:
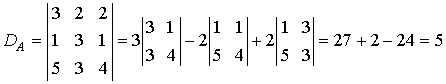
Находим алгебраические дополнения элементов этого определителя:
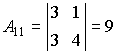 ,
, 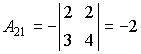 ,
, 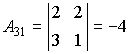
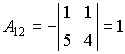 ,
, 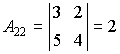 ,
, 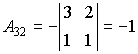
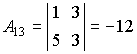 ,
,  ,
, 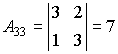
Следовательно,
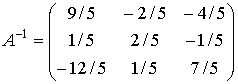
Ранг матрицы равен порядку наибольшего минора, отличного от нуля.
Теорема Кронекера-Капелли – система совместна, то есть имеет только одно решение, когда ранг матрицы системы равен рангу расширенной матрицы.
Метод Жордана - Гаусса
|
Решим систему уравнений |
|
|
|
2 |
x1 |
+ |
|
x2 |
|
- |
x3 |
= |
|
2 |
|
|
3 |
x1 |
+ |
|
x2 |
- |
2 |
x3 |
= |
|
3 |
|
|
|
|
x1 |
|
+ |
|
x3 |
= |
|
3 |
|||
|
Процесс решения системы уравнений методом Жордана - Гаусса, состоит из двух этапов. |
|
На первом этапе (прямой ход) система приводится к ступенчатому виду, путем последовательного исключения переменных. |
|
На втором этапе решения (обратный ход) мы будем последовательно находить переменные из получившейся ступенчатой системы. |
|
Последовательность исключения переменных, Вы можете проследить по выделенным серыми прямоугольниками коэффициентам системы. |
|
На каждом шаге решения справа располагается расширенная матрица, эквивалентная системе уравнений. Расширенная матрица - это просто форма записи нашей системы уравнений, и ничего более (каждая строка матрицы представляет собой уравнение системы). Данная форма решения менее наглядная, но позволяет не переписывать каждый раз переменные, что существенно экономит время. |
|
Прямой ход. |
|
Запишем исходную систему. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Исключим переменную x1 из всех уравнений, за исключением первого. |
|
Поменяем местами уравнения 1 и 3 (порядок уравнений в системе не имеет значения). |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Умножим коэффициенты уравнения 1 на -3 и прибавим получившееся уравнение к уравнению 2. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Умножим коэффициенты уравнения 1 на -2 и прибавим получившееся уравнение к уравнению 3. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Исключим переменную x2 из последнего уравнения. |
|
Поменяем местами уравнения 2 и 3 (порядок уравнений в системе не имеет значения). |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Умножим коэффициенты уравнения 2 на -1 и прибавим получившееся уравнение к уравнению 3. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Обратный ход. |
|
Коэффициенты уравнения 3 разделим на -2. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Исключим переменную x3 из всех уравнений, за исключением последнего. |
|
Умножим коэффициенты уравнения 3 на -1 и прибавим получившееся уравнение к уравнению 1. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Умножим коэффициенты уравнения 3 на 3 и прибавим получившееся уравнение к уравнению 2. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ответ : |
|
|
|
x1 |
= |
|
2 |
|
|
|
|
x2 |
= |
- |
1 |
|
|
|
|
x3 |
= |
|
1 |
|
-
Векторы: определение. Коллинеарные векторы, ортогональные векторы. Линейные операции над векторами и их свойства, модуль вектора, направляющие косинусы вектора. Скалярное, векторное, смешанное произведение векторов. Некоторые приложения скалярного векторного и смешанного произведений.
Вектор,
представленный направленным отрезком,
идущим от точки A к
точке B,
обозначается так: ![]() .
.
Два вектора называются коллинеарными, если они параллельны одной прямой или лежат на ней.
Два вектора называются ортогональными, если угол между ними прямой.
Сложение векторов: вектором суммы называется вектор, соединяющий начало первого вектора с концом второго. Свойства: переместительное, сочетательное, распределительное.
Произведение вектора на число: при произведении вектора на число его координаты умножаются на это число.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
Модуль вектора (длина вектора) |a| в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат.
Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:
![]()
где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.
Сумма квадратов направляющих косинусов равна 1.
Скалярным
произведением двух векторов называется
число, равное произведению модулей этих
векторов на косинус угла между ними.
![]()
Если
векторы ![]() и
и ![]() заданы
своими координатами:
заданы
своими координатами:
![]() ,
, ![]() ,
,
то
их скалярное произведение может быть
вычислено по формуле
![]() .
.
Отсюда
следует необходимое условие
перпендикулярности двух векторов
![]()
Свойства
скалярного произведения:
![]()
![]()
![]()
![]()
Геометрический смысл скалярного произведения:
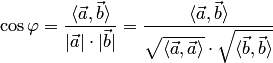
Физический смысл скалярного произведения:
Скалярное произведение двух векторов – есть работа одного из них на пути, равном другому. A = F * MN
Векторным
произведением двух векторов
называется вектор
![]() ,
удовлетворяющии следующим условиям:
,
удовлетворяющии следующим условиям:
-
Модуль вектора
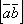 равен
равен 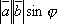 ,
где
,
где 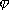 -
угол между векторами
-
угол между векторами 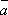 и
и  ;
; -
Вектор
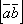 перпендикулярен
к каждому из вектора
перпендикулярен
к каждому из вектора 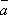 и
и 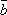 ;
; -
Векторы
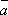 ,
,
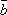 и
и
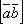 образуют правую тройку, то есть, если
смотреть из конца вектора
образуют правую тройку, то есть, если
смотреть из конца вектора
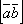 ,
то кратчайший поворот от
,
то кратчайший поворот от
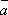 к
к
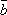 должен
проходить против часовой стрелки.
должен
проходить против часовой стрелки.
Свойства векторного произведения:
![]()
![]()
Условие коллинеарности двух векторов: a II b a x b = 0
Если
система координатных осей правая и
векторы ![]() и
и ![]() заданы
в этой системе своими координатами:
заданы
в этой системе своими координатами:
![]() ,
, ![]() ,то
векторное произведение вектора
,то
векторное произведение вектора ![]() на
вектор
на
вектор ![]() определяется
формулой
определяется
формулой
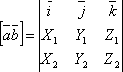 .
.
Геометрический смысл векторного произведения:
Длина векторного произведения равна площади параллелограмма, построенного на векторах a и b, как на сторонах.
Физический смысл векторного произведения:
Если твердое тело закреплено в точке О, а к другой точке N приложить силу F, то возникает вращательный момент М. M = F x ON
Смешанное произведение векторов называется скалярное произведение векторного произведения первых двух векторов на третий. a * b* c = (a x b) * c.
Свойства смешанного произведения:
-
Произведение не изменится, если переставлять вектора в круговом порядке.
-
a*b*c = -a*c*b или a*b*c= -b*a*c
Если
векторы ![]() ,
, ![]() ,
, ![]() заданы
своими координатами:
заданы
своими координатами:
![]() ,
, ![]() ,
, ![]() ,
,
то
смешанное произведение определяется
формулой
 .
.
Условие компланарности: abc = 0, если a≠0, b≠0, c≠0
Геометрический смысл смешанного произведения: смешанное произведение равно объёму параллелепипеда, построенного на векторах a,b,c, как на рёбрах.
