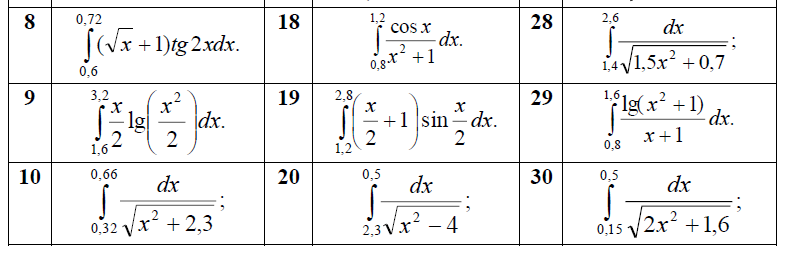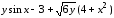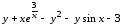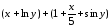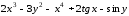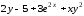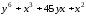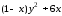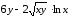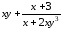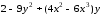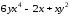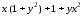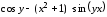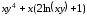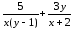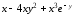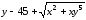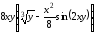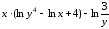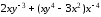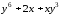Matlab / 04 Диффер. и интегрир +

Лабораторная работа № 4

Matlab: Дифференцирование и интегрирование

Цель работы: получение навыков дифференцирования и интегрирования функций в пакете Matlab.

Теоретические сведения

Дифференцирование

Аналитическое дифференцирование. Для вычисления производных в символьном виде от выражения 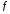служит функция diff(f).

Создадим символьное выражение:

syms a x;

f = sin(a*x);

тогда diff(f) приведет к дифференцированию 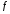по ее символьной переменной (в данном случае это ):

ans = cos(a*x)*a

Для взятия производной по переменной , явно укажем: diff(f,a). Данное выражение вернет df/da:

ans = cos(a*x)*x

Чтобы найти производные более высоких порядков, необходимо указать порядок производной. Например, производная второго порядка:

diff(f,2); или diff(f,x,2);

ans = -sin(a*x)*a^2

и

diff(f,a,2);

вернет ans = -sin(a*x)*x^2

Функция diff в качестве входного параметра может принимать символьную матрицу. В таком случае дифференцирование происходит поэлементно:

syms a x;

A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)];

Т. е. матрица А имеет вид:

A =

[ cos(a*x), sin(a*x)]

[ -sin(a*x), cos(a*x)]

Тогда результат команды diff(A) будет:

ans =

[ -sin(a*x)*a, cos(a*x)*a]

[ -cos(a*x)*a, -sin(a*x)*a]

Численное дифференцирование. Численное дифференцирование строится на использовании аппарата конечных разностей и соответствующего многообразия аппроксимаций. Используются функции:

diff(X) — для вектора X вычисление первых конечных разностей [X(2)-X(1) X(3)-X(2) ... X(n)-X(n-1)], а для матрицы X вычисление первых конечных разностей между столбцами [X(2:n,:) - X(1:n-1,:)];

diff(X, n) — вычисление конечных разностей n-го порядка;

diff(X, n, dim) — вычисление конечных разностей n-го порядка по указанному измерению.

Интегрирование

Аналитическое интегрирование. Функция int(f,x) аналитически вычисляет интеграл от функции по символьной переменной :

syms x;

int(sin(x)./x.^2,x)

ans =

-sin(x)/x+cosint(x)

Функция int(f,x,a,b) численно вычисляет интеграл от функции 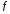по символьной переменной в границах :

int(sin(x)./x.^2,x,0.1,pi)

ans =

cosint(pi)+10*sin(1/10)-cosint(1/10)

>> cosint(pi)+10*sin(1/10)-cosint(1/10)

ans =

2.7999

Численное интегрирование. Численное интегрирование в Matlab выполняется с помощью функций:

trapz — интегрирование методом трапеций;

quad, quad8 — вычисление интегралов методом квадратур.

Интегрирование методом трапеций.

В Matlab данную формулу реализует функция trapz(x, y), которая вычисляет интеграл от функции y по переменной x, используя метод трапеций. Аргументы x и y могут быть одномерными массивами одинакового размера, либо массив y может быть двумерным, но тогда должно выполняться условие size(y, 1) = length(x). В последнем случае вычисляется интеграл для каждого столбца.

Функция trapz(y) вычисляет интеграл, предполагая, что шаг интегрирования постоянен и равен единице; в случае, когда шаг h отличен от единице, но постоянен, достаточно вычисленный интеграл умножить на h.

Пример 1. Вычислим интеграл: 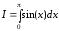. Его точное значение равно двум.

Выберем равномерную сетку:

x = 0:pi/100:pi;      

y = sin(x);

тогда оба интеграла

I = trapz(x, y)

и

I = pi/100*trapz(y)

дают одинаковый результат:

I =     1.9998

Образуем неравномерную сетку, используя генератор случайных чисел:

x = sort(rand(1,101)*pi);

y = sin(x);

I = trapz(x, y)

I = 1.9987

Результат еще менее точен, поскольку максимальный из шагов max(diff(x)) равен 0,1810.

Вычисление интегралов методом квадратур. Квадратура — это численный метод вычисления площади под графиком функции, то есть вычисление определенного интеграла вида:

.

Функции quad и quad8 используют разные квадратурные формулы. Функция quad использует квадратурные формулы Ньютона-Котеса 2-го порядка (правило Симпсона), а функция quad8 — формулы 8-го порядка. При наличии в подынтегральной функции особенностей типа:

,

предпочтительнее использовать процедуру quad8.

Функции [I, cnt] = quad(‘имя функции‘, a, b) и [I, cnt] = quad8(‘имя функции‘, a, b) вычисляют интеграл от заданной функции. Переменная cnt содержит информацию о том, сколько раз в процессе интегрирования вычислялась подынтегральная функция.

Функции [I, cnt] = quad(‘имя функции‘, a, b, tol) и [I, cnt] = quad8(‘имя функции‘, a, b, tol) вычисляют интеграл с заданной относительной погрешностью tol. По умолчанию tol = 1e-3.

Функции [I, cnt] = quad(‘имя функции‘, a, b, tol, trace) и [I, cnt] = quad8(‘имя функции‘, a, b, tol, trace), когда аргумент trace не равен нулю, строят график, показывающий ход вычисления интеграла.

Пример 2. Вычислим интеграл: 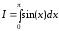. Его точное значение равно двум.

[I, cnt] = quad('sin', 0, pi)	[I, cnt] = quad('sin', 0, pi, 1e-4, 1)
I = 2.0000	I = 2.0000
cnt = 17	cnt = 33

Как следует из анализа полученных данных, при увеличении точности вычисления на порядок почти вдвое увеличивается трудоемкость расчетов. График с результатами промежуточных расчетов показан на рис. 1.

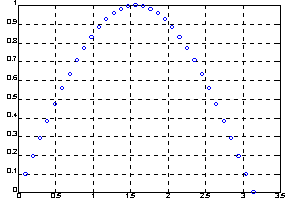
Рис. 1.

Функции quad и quad8 используют рекурсивный вызов. Для того чтобы предотвратить бесконечную рекурсию при вычислении сингулярных интегралов, глубина рекурсии ограничена уровнем 10. При достижении этого ограничения выдается сообщение: «Recursion level limit reached in quad. Singularity likely» (В процедуре quad достигнута предельная глубина рекурсии. Функция, возможно, сингулярная).

Функции quad и quad8 не позволяют интегрировать функции с особенностями типа:

.

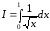В этом случае рекомендуется выделить такие члены и проинтегрировать их аналитически, а к остатку применить процедуры quad и quad8.

Задания

Все задания рекомендуется выполнять в m-файлах.

Задание 1. Для функции , равной следующему выражению:

№	Выражение	№	Выражение
1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

аналитически найдите первую и вторую частные производные по x и по y.

Задание 2. Аналитически найдите производные сложных функций:

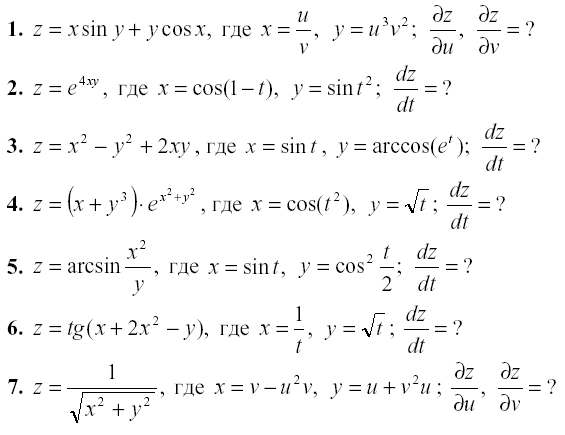
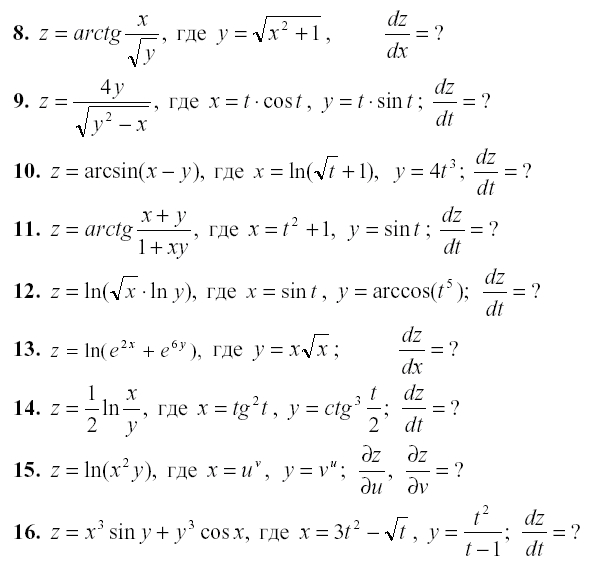
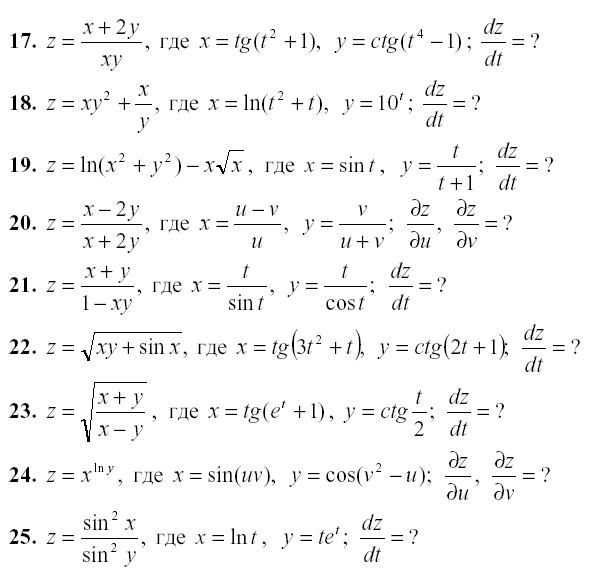
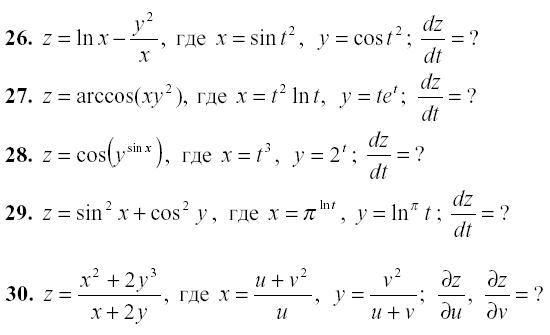
При этом необходимо использовать функцию subs для замены:

z1=subs(z, [x y], [u/v u^3*v^2]),

где z — исходное выражение, в которое входят символьные переменные x и y, заменяемые на выражения u/v и u^3*v^2 соответственно.

Задание 3. Задайте вектор 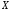размерности 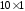с произвольными значениями элементов. Численно найдите производные — вычислите первые и третьи конечные разности.

Рис. 2.

Задание 4. С помощью функции int найдите неопределенные интегралы от функции :

Задание 5. Найдите определенные интегралы с помощью функций int, trapz, quad, quad8. Сравните результаты.

12