
Часть І. Элементы линейной алгебры и аналитической геометрии.
Глава 3. Элементы векторной алгебры
§1. Векторы на плоскости и в пространстве
Определение 1. Вектором называется направленный отрезок, у которого определены начало и конец.

Определение 2. Длиной или модулем вектора называется длина отрезка АB, порождающего данный вектор.
![]()
В математике рассматривают свободные векторы, которые в пространстве можно перемещать параллельно самим себе.
Определение 3. Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых и компланарными, если они лежат в одной плоскости или параллельных плоскостях.

Действия над векторами в геометрической форме:
Векторы можно умножить на постоянное число λ ≠ 0

Частный
случай:
если
![]() умножить на
умножить на![]() ,
то получится
,
то получится
противоположный
вектор
![]() .
.
Векторы можно складывать:
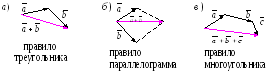
Если конец последнего вектора попадают в начало первого, то сумма векторов равна нулю.
Векторы можно вычитать:
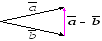
![]()
Координаты вектора
Построим
![]() :
:

Определение
4. Координатами
вектора
![]() ,
выходящего из начала координат называются
координаты его конечной точкиМ.
,
выходящего из начала координат называются
координаты его конечной точкиМ.
![]()
![]() .
.
Если вектор задан двумя точками, то:
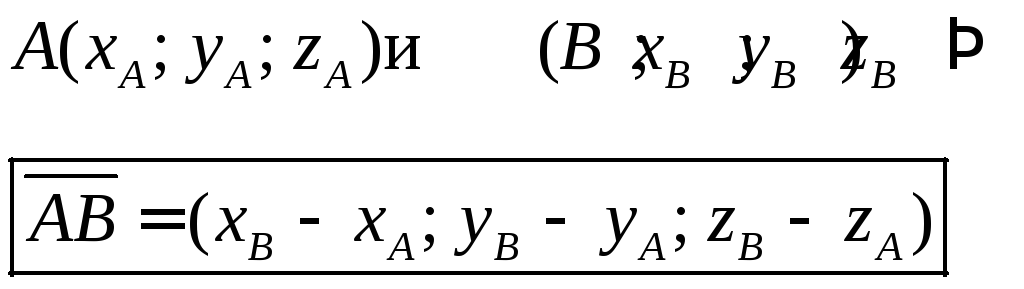
Действия над векторами в координатной форме:
Если векторы заданы координатами, то:
1)
![]()
2)
![]()
Определение 5. Длина вектора равна корню квадратному из суммы
квадратов его координат.
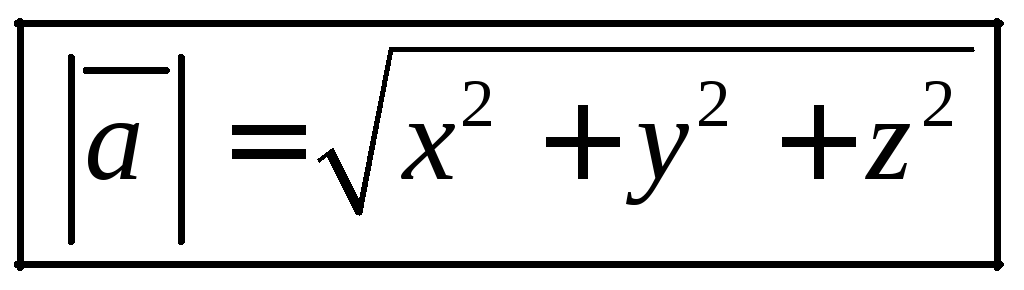
Координатный базис:
В системе
![]() векторы
векторы![]() и
и![]() образуют базис
образуют базис![]() (двухмерное пространство):
(двухмерное пространство):
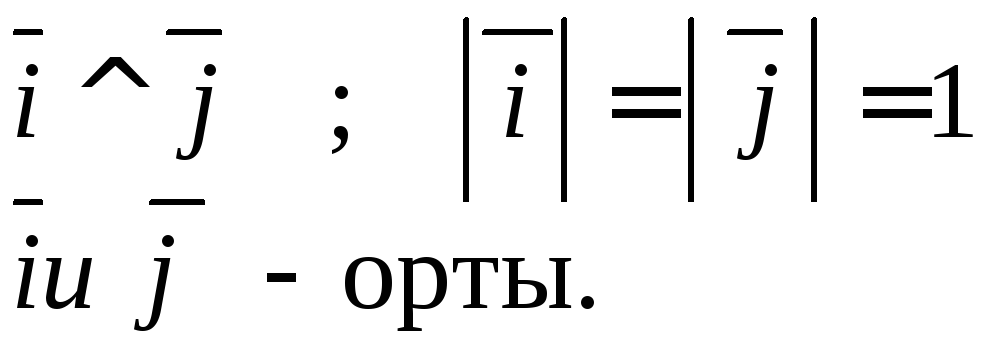
В системе
![]() векторы
векторы![]() ,
,![]() ,
,![]() образуют базис
образуют базис![]() (трехмерное
(трехмерное
пространство):
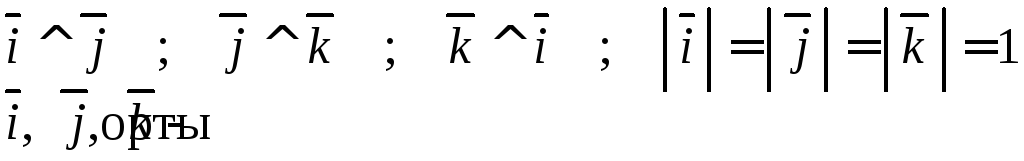
Любой вектор
![]() пространства можно разложить по
векторам.
пространства можно разложить по
векторам.
В
![]() :
:
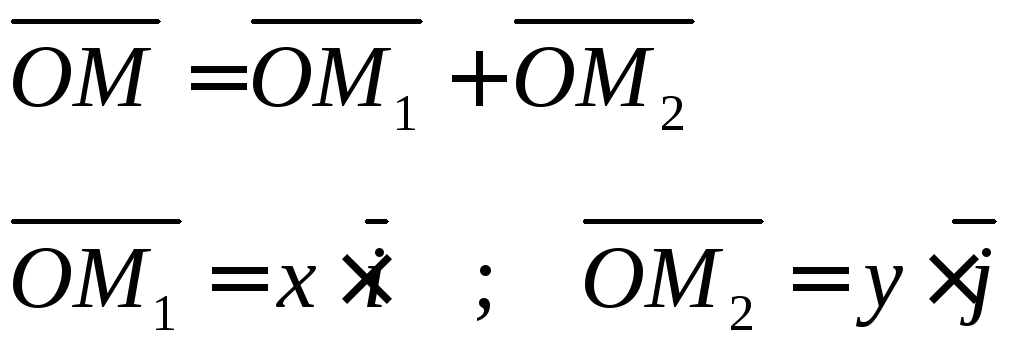
![]()
![]()
Аналогично в
пространстве
![]() :
:
![]()
Определение 6. Выражения (1) и (2) называются разложением
вектора по координатному базису.
Определение
7.
![]() - называютсякомпонентами
- называютсякомпонентами
вектора на соответствующие оси.
§2. Скалярное произведение векторов
Определение
1.
Скалярным
произведением
двух ненулевых векторов
![]() и
и![]() называется число, равное произведению
их модулей на
называется число, равное произведению
их модулей на![]() угла между ними.
угла между ними.
![]()

Свойства скалярного произведения:
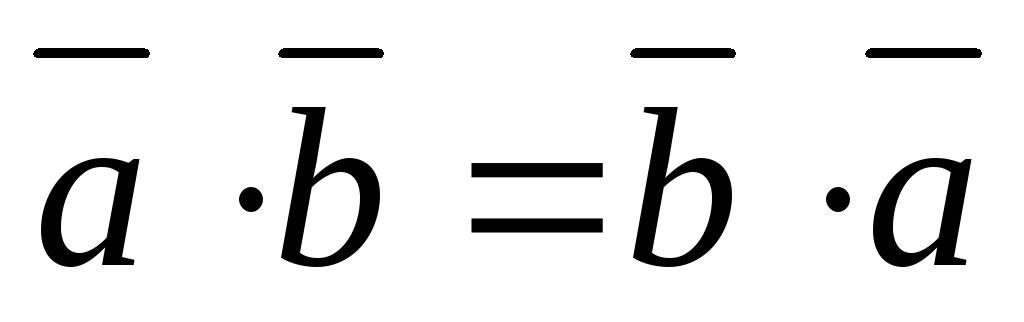 - произведение
векторов коммутативно.
- произведение
векторов коммутативно.
Скалярный квадрат вектора равен квадрату его модуля:
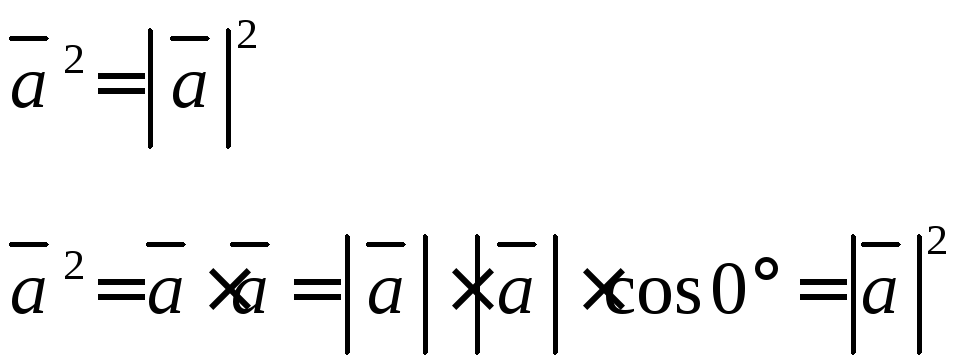
![]()
![]()
Если
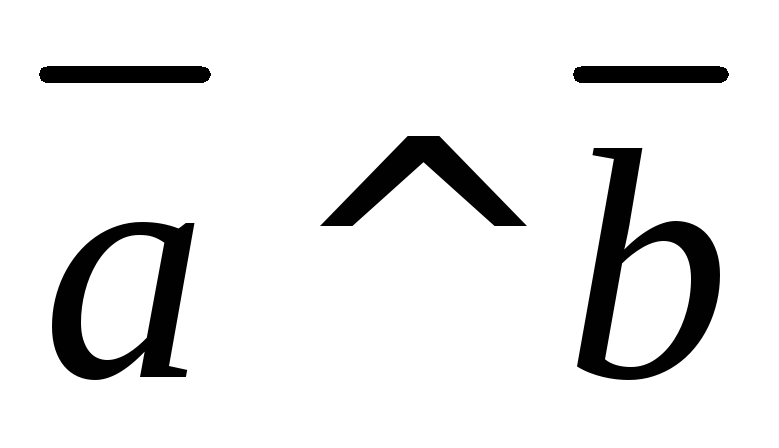 ,
то их скалярное произведение равно
нулю:
,
то их скалярное произведение равно
нулю:
![]()
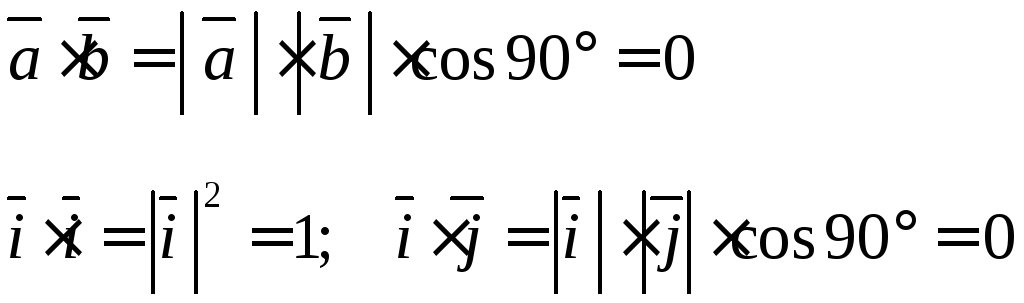
Причем, произведение одноименных орт равно единице, а разноименных орт равно нулю.
-

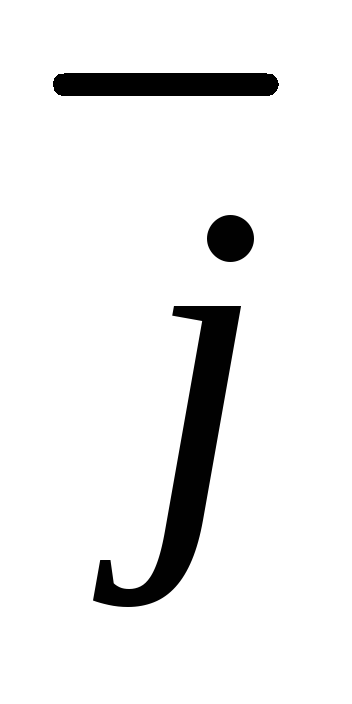
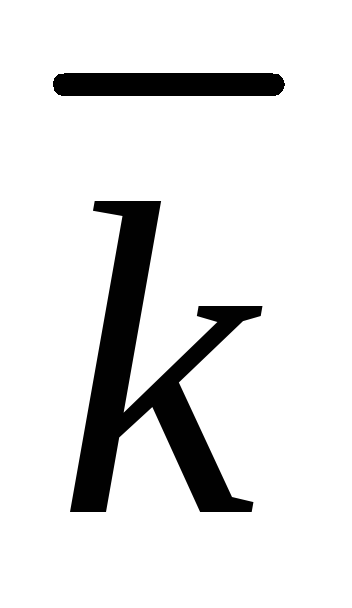

1
0
0
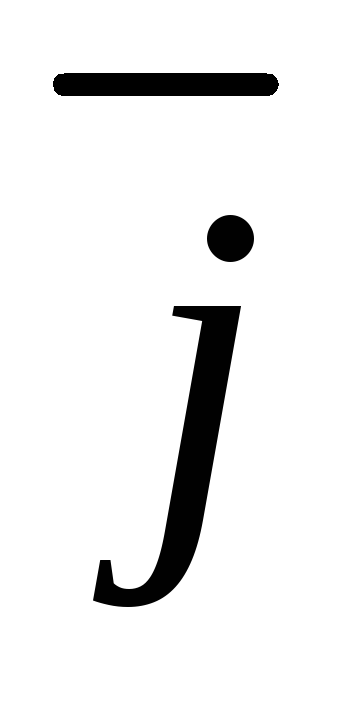
0
1
0
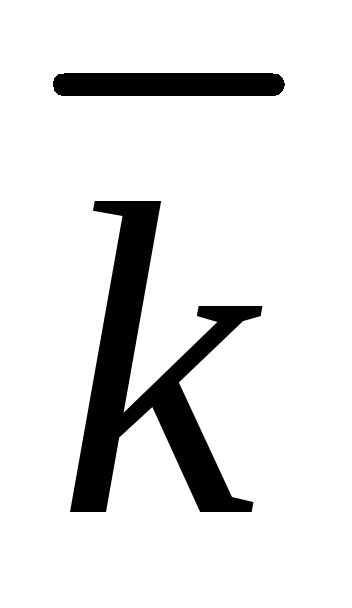
0
0
1
Скалярное произведение векторов, заданных координатами равно сумме произведений одноименных координат:
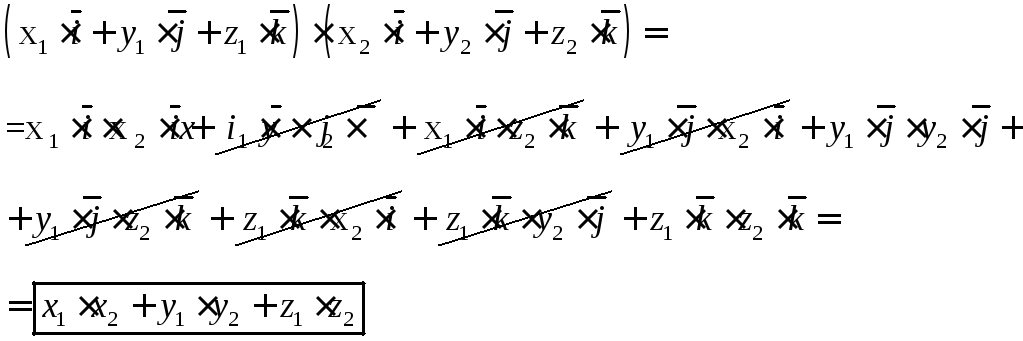
Из формулы скалярного произведения векторов можно найти
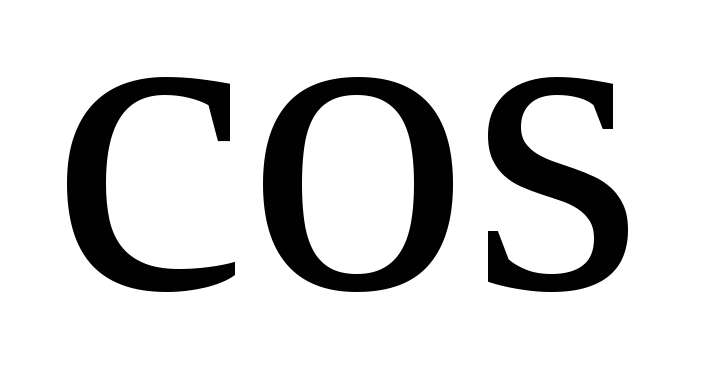 угла между двумя векторами:
угла между двумя векторами:
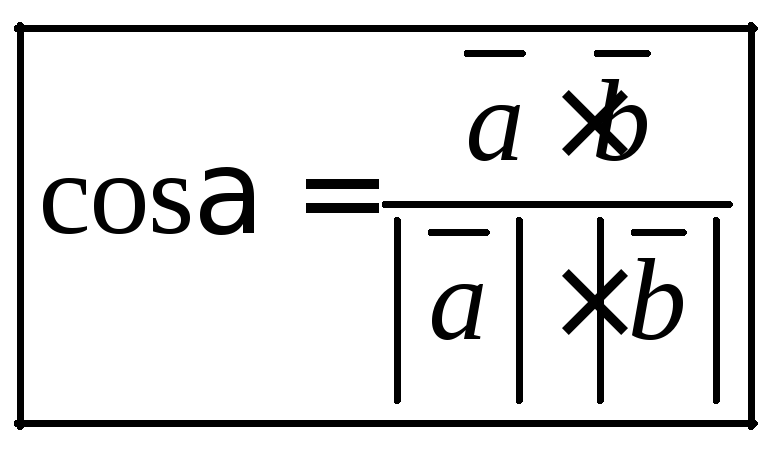
В координатной форме:
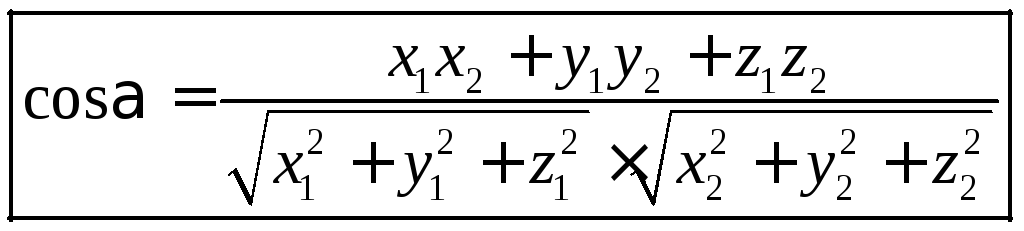
Пример:
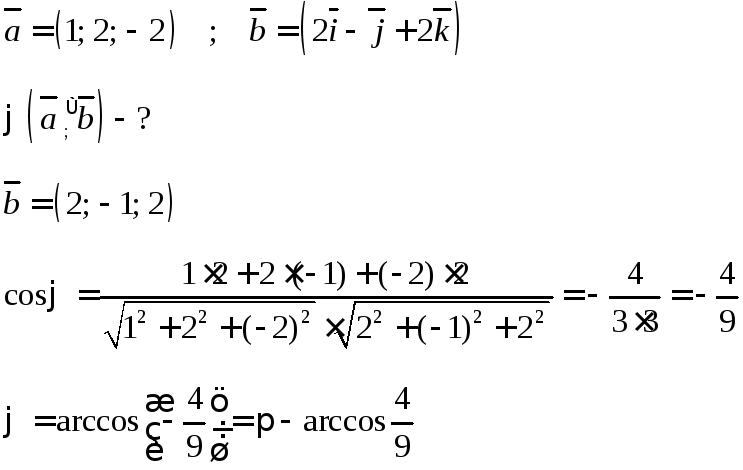
§3. N- мерный вектор
Определение
1. Упорядоченный
набор чисел, записанный в виде
![]() ,
называетсяn
- мерным вектором,
где
,
называетсяn
- мерным вектором,
где
![]() - его координаты или компоненты
- его координаты или компоненты![]() .
.
Понятие n
- мерного вектора широко используется
в экономике: некоторый набор товаров
можно охарактеризовать вектором
![]() ,
а соответствующие цены - вектором
,
а соответствующие цены - вектором![]() .
.
Векторы можно:
умножать на действительное число
![]() ;
;
складывать
![]() .
.
Эти операции обладают следующими свойствами:
1.
![]() - переместительное (коммутативное).
- переместительное (коммутативное).
2.
![]() - сочетательное (ассоциативное)
- сочетательное (ассоциативное)
3.
![]() - ассоциативное относительно числового
множителя
- ассоциативное относительно числового
множителя
4.
![]() - распределительное (дистрибутивное)
- распределительное (дистрибутивное)
5.
![]() - дистрибутивное относительно суммы
числовых
- дистрибутивное относительно суммы
числовых
множителей.
Существует нулевой вектор
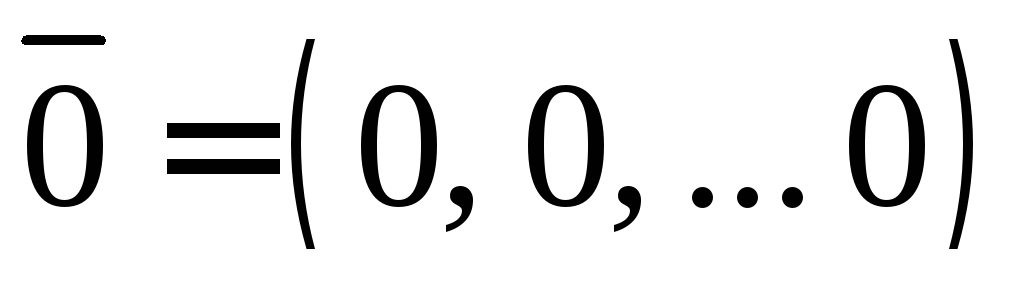 такой, что
такой, что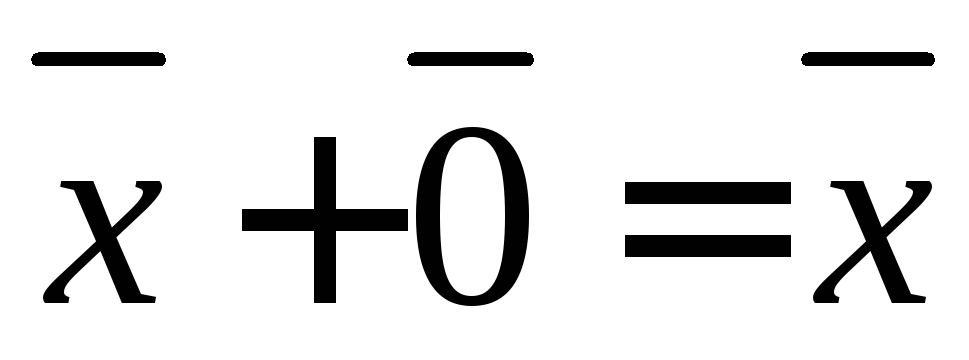
Для любого вектора
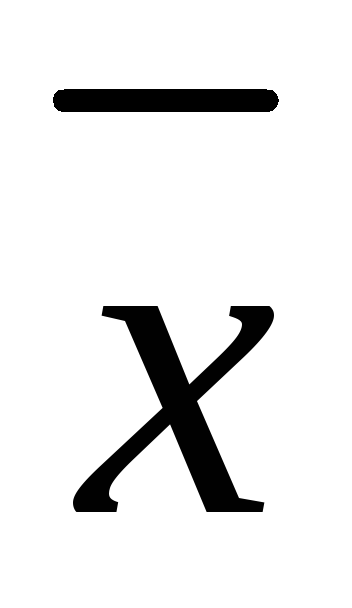 существует противоположный вектор
существует противоположный вектор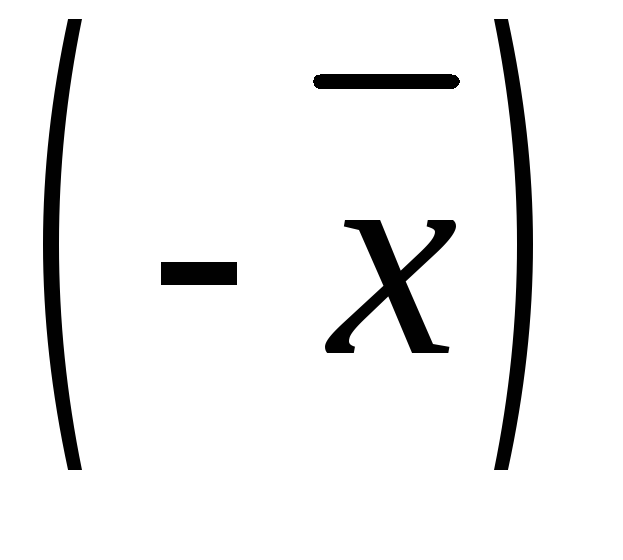 такой, что
такой, что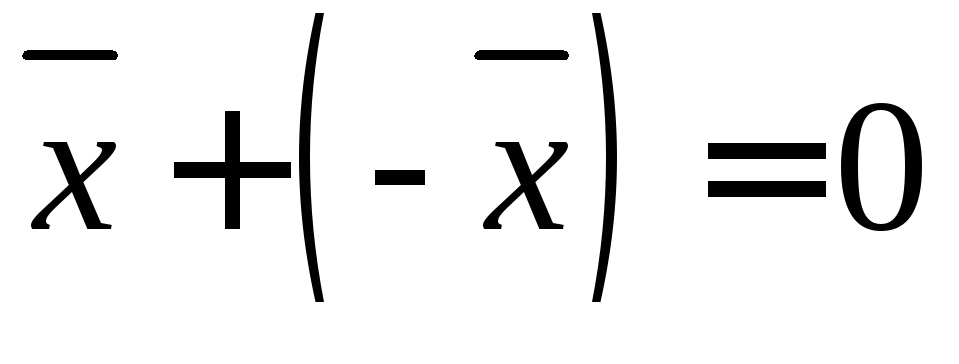
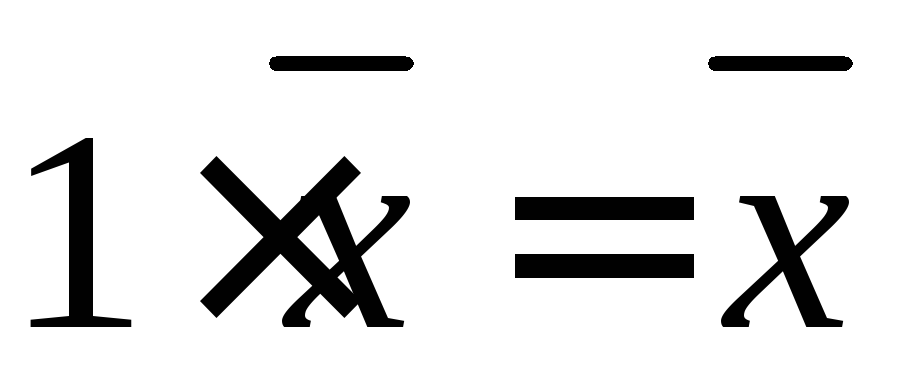 - для любого вектора
- для любого вектора
 .
.
Определение
2. Множество
векторов с действительными компонентами,
в котором определены действия
![]() и
и![]() ,
удовлетворяющие
8- ми свойствам (аксиомам), называется
векторным
пространством.
Если под
,
удовлетворяющие
8- ми свойствам (аксиомам), называется
векторным
пространством.
Если под
![]() понимать
элементы любой природы, то множество
называется линейным
пространством.
понимать
элементы любой природы, то множество
называется линейным
пространством.
Определение
3. Вектор
![]() называетсялинейной
комбинацией
векторов
называетсялинейной
комбинацией
векторов
![]() векторного пространства
векторного пространства![]() ,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
![]()
Определение
4. Векторы
![]() векторного пространства
векторного пространства![]() называютсялинейно
зависимыми,
если существуют такие числа
называютсялинейно
зависимыми,
если существуют такие числа
![]() ,
не равные одновременно нулю, что:
,
не равные одновременно нулю, что:
![]()
В противном случае векторы называются линейно независимыми (два неколлинеарных вектора).
Пример 1:
Выяснить, являются ли векторы
![]() линейно зависимыми.
линейно зависимыми.
Решение:
Составим векторное
равенство:
![]()
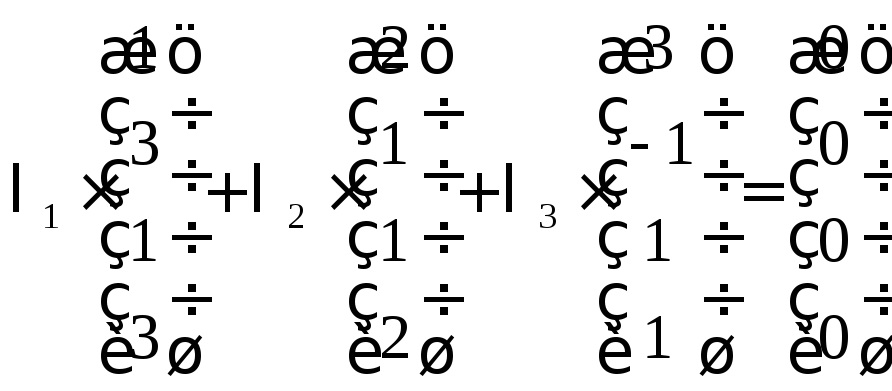 .
.
Задача свелась к решению системы:
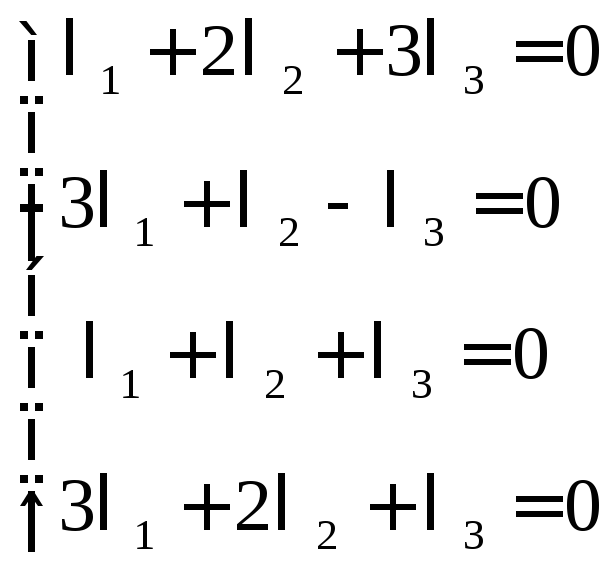
![]()
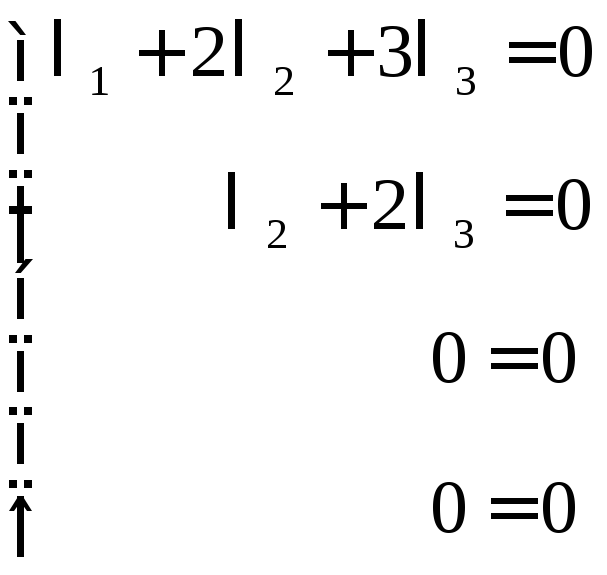
Следовательно, система имеет множество решений:
![]() ,
где
,
где
![]() - произвольное действительное число.
- произвольное действительное число.
Итак, для данных векторов условие (2) выполняется не только при
![]() эти векторы линейно
зависимые.
эти векторы линейно
зависимые.
Пример
2: Даны три
вектора:
![]() .
.
Доказать,
что векторы
![]() и
и![]() линейно независимы и выразить вектор
линейно независимы и выразить вектор![]() через
через![]() и
и![]() .
.
Решение:
1) Докажем линейную независимость векторов:
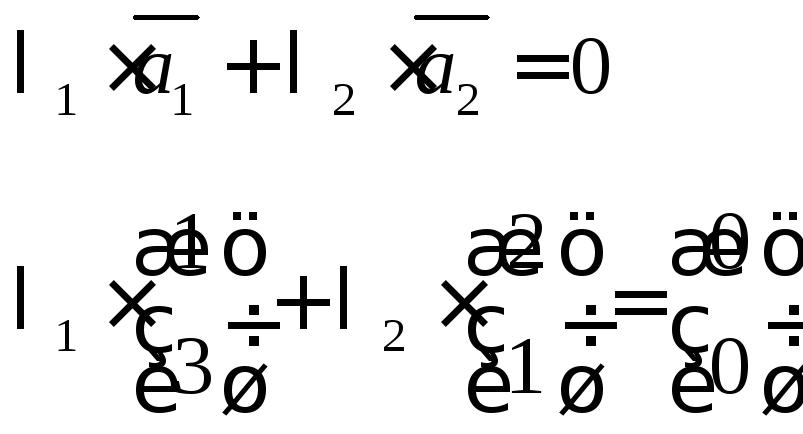
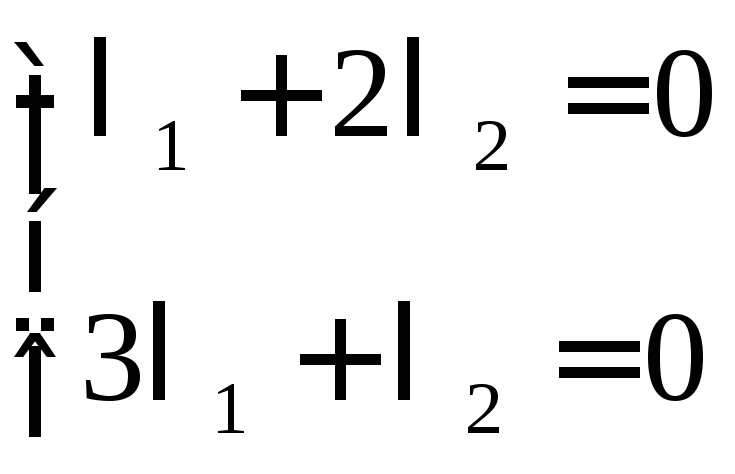
Такая система всегда имеет тривиальное нулевое решение.
Убедимся, что других решений эта система не имеет:
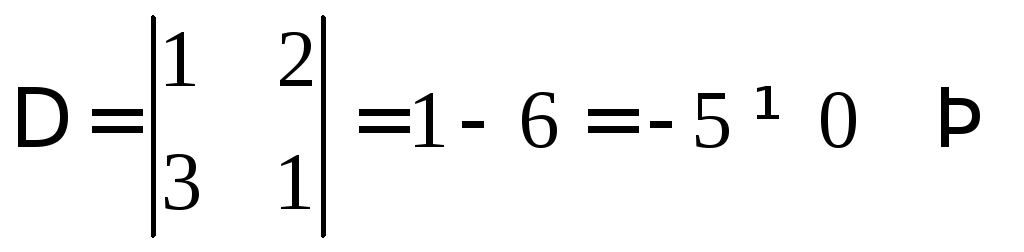 система имеет
только нулевое решение, значит, векторы
линейно независимы.
система имеет
только нулевое решение, значит, векторы
линейно независимы.
2)Выразим вектор
![]() :
:
![]()
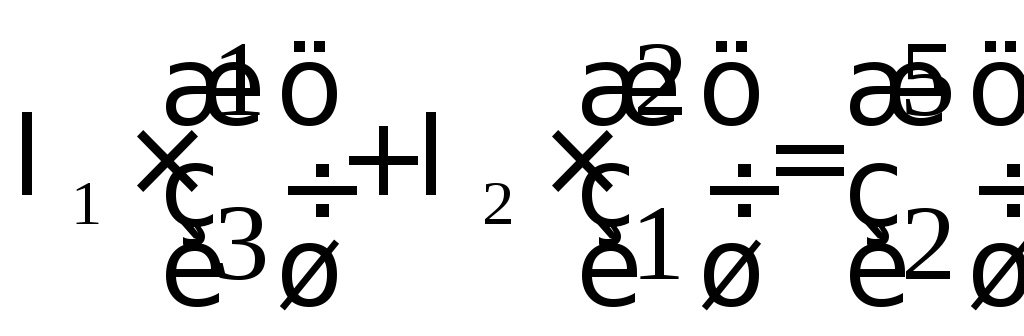
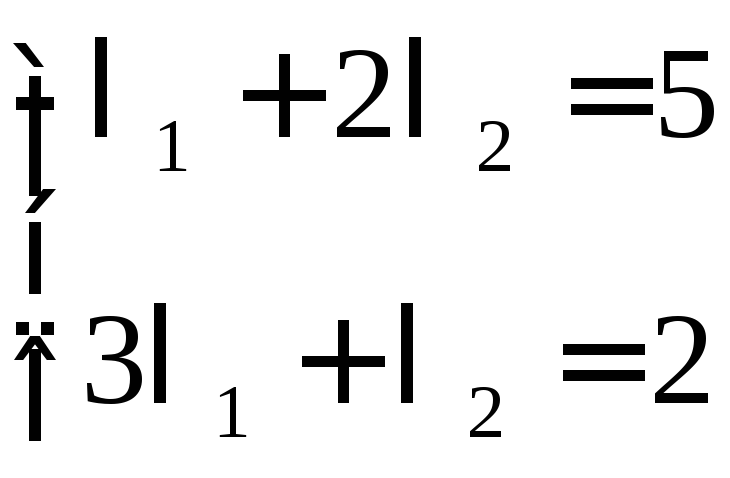
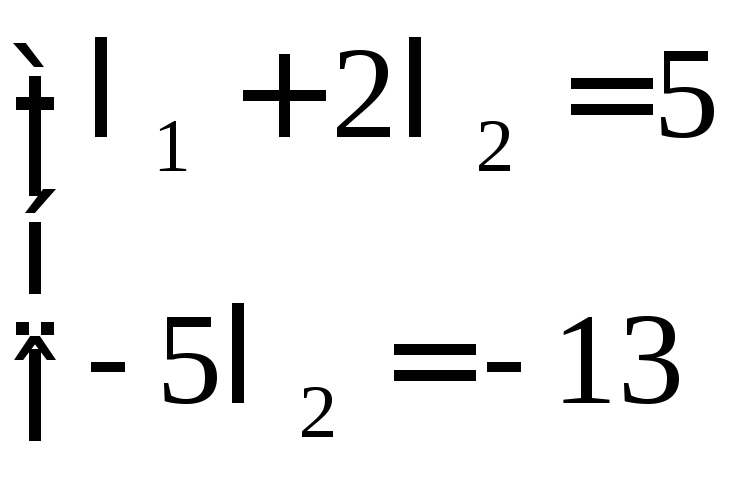
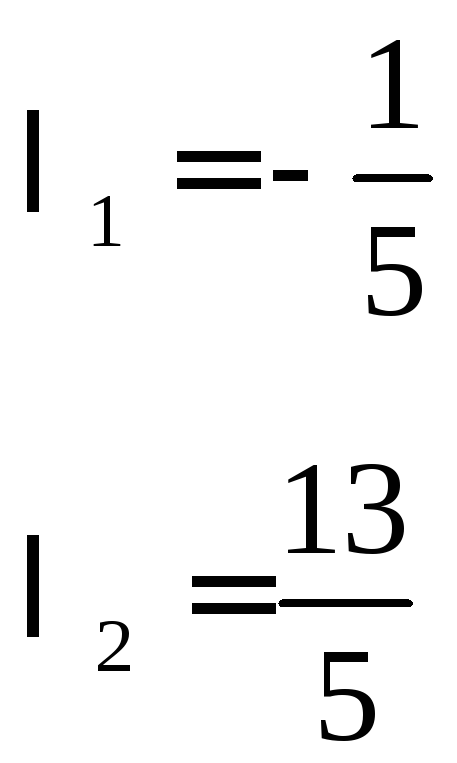
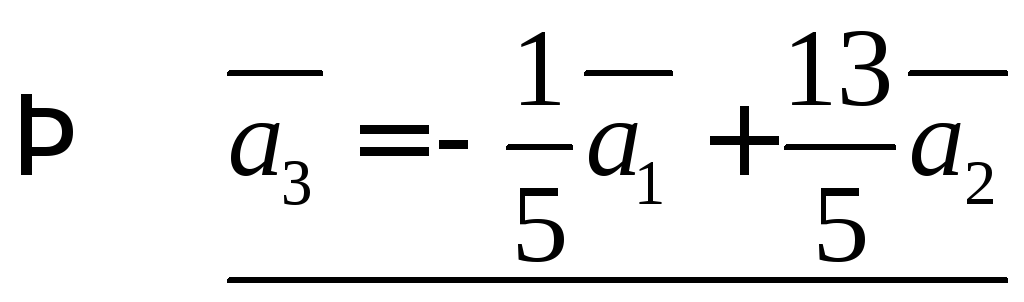
Определение 5. Линейное пространство R называется n- мерным, если в нем существует n - линейно независимых векторов.
Определение 6. Максимальное число (n) содержащихся в пространстве R линейно независимых векторов называется размерностью пространства и обозначается dim (R).
Определение 7. Совокупность n линейно независимых векторов пространства R называется базисом.
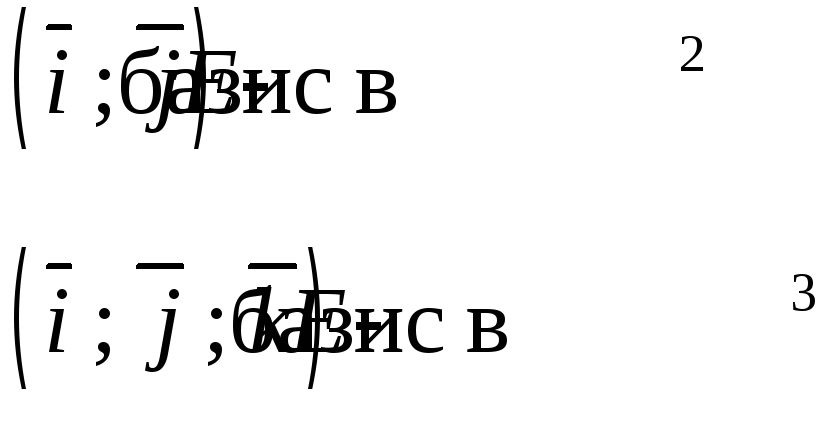
Определение
8. Если
![]() - базис пространстваR,
то вектор
- базис пространстваR,
то вектор
![]() называетсяразложением
вектора
называетсяразложением
вектора
![]() по базису, а числа
по базису, а числа![]() -координатами
вектора
-координатами
вектора
![]() относительно этого базиса.
относительно этого базиса.
Пример:
Показать,
что векторы
![]() ,
заданные в базисе
,
заданные в базисе![]() ,
сами образуют базис.
,
сами образуют базис.
Решение:
Векторы
![]() образуют базис, если они линейно
независимы.
образуют базис, если они линейно
независимы.
Составим векторное равенство:
![]()

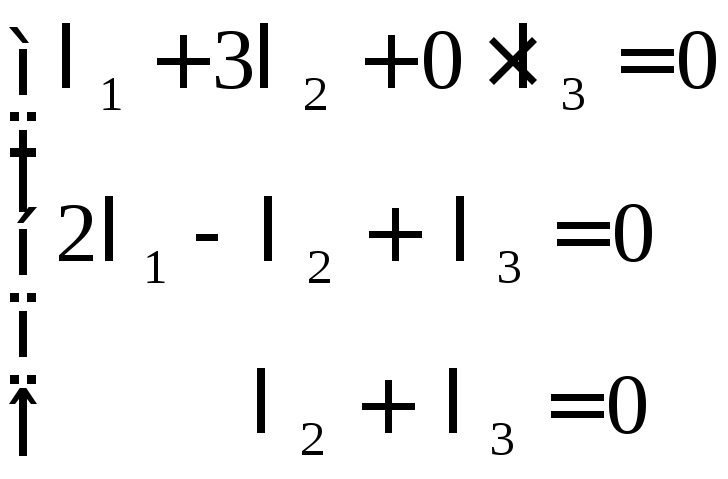
Такая система всегда имеет тривиальное, нулевое решение. Убедимся, что других решений система не имеет:
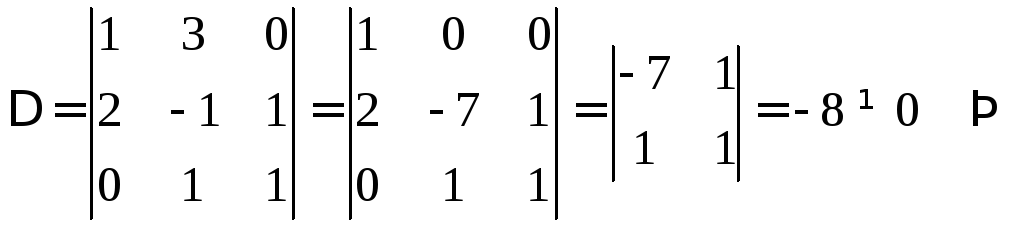 система имеет
только нулевое решение, значит, векторы
система имеет
только нулевое решение, значит, векторы
![]() образуют систему линейно независимых
векторов и составляют базис.
образуют систему линейно независимых
векторов и составляют базис.
Теорема.
Если
![]() - система линейно независимых векторов
пространстваR
и любой вектор
- система линейно независимых векторов
пространстваR
и любой вектор
![]() линейно выражается через
линейно выражается через![]() ,
то пространствоR
является n
- мерным, а векторы
,
то пространствоR
является n
- мерным, а векторы
![]() - его базисом.
- его базисом.

(без доказательства).
