
- •Таблица производных
- •Производной n-го порядка называется производная от производной (n –1)-го порядка.
- •Возрастание и убывания функций
- •Экстремум функции
- •Необходимое и достаточное условия экстремума
- •Схема исследования функции на экстремум
- •Выпуклость функции. Точки перегиба.
- •Теорема. Функция выпукла вниз (вверх) на промежутке Х тогда и только тогда, когда
- •Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла
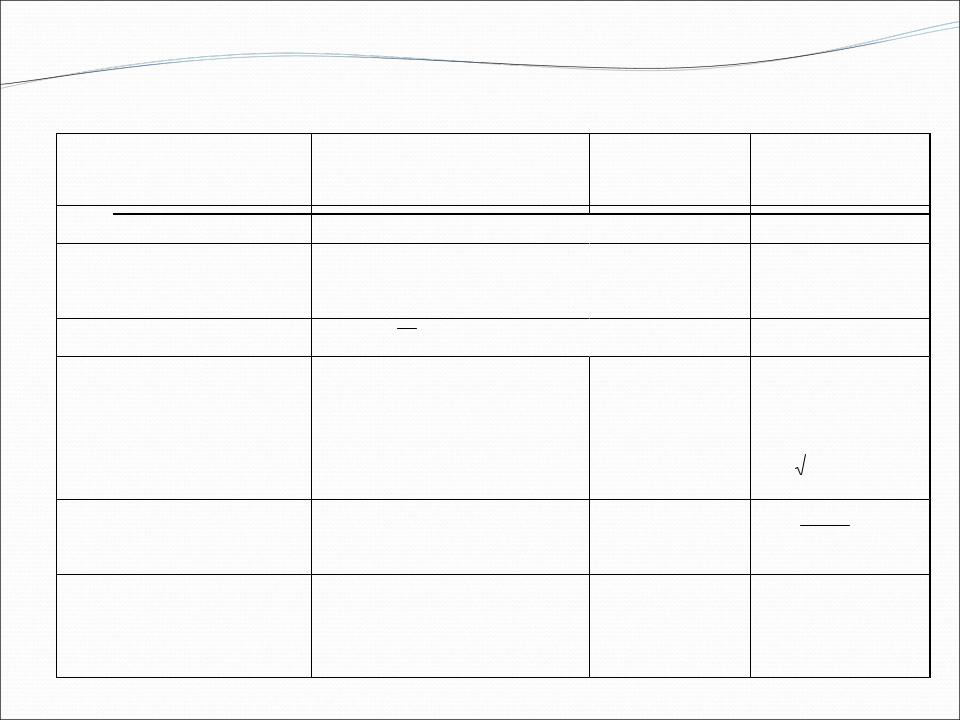
Таблица производных
№ Функция у
1 |
C |
|
2 |
x |
|
3 |
1 |
|
4 |
||
u |
||
5 |
||
eu |
||
6 |
||
alnu |
||
|
u |
7 logau
8 un
Производная у
0
1
1 u u2
eu u
(1u/u) u a ln a u
(1/ u lna) u
nun-1 u
№ Функция у
9  sin u
sin u
10  cos u
cos u
11  tg u
tg u
12  ctg u
ctg u
13 arcsin u
14 arccos u
15 arctg u
16 arcctg u
Производна я у
cos u u
sin u u
|
1 |
|
|
u |
||
|
cos2 u |
|||||
|
|
|
||||
|
|
1 |
u |
|||
sin2 u |
||||||
1 |
|
|
|
u |
||
|
|
|
|
|
|
|
|
1 u2 |
|||||
(1/(1+uu2)) u

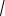 1 u2
1 u2
- (1/(1+u2)) u

Производной n-го порядка называется производная от производной (n –1)-го порядка.
Обозначение производных: ( х) второго порядка, ( х) – третьего
порядка. Производные более высокого порядка обозначаются следующим образом: (n) ( х) – производная n-го порядка.
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида [0/0] [ / ], то:
lim |
f (x) |
lim |
f '(x) |
. |
g(x) |
|
|||
x x0 |
x x0 |
g'(x) |
||
|
|
|
||
( x ) |
|
( x ) |
|
|

Возрастание и убывания функций
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.
Пример 1. Найти интервалы монотонности функции у = х2 4х + 4.

Экстремум функции
Точка х0 называется точкой минимума функции ( х), если в некоторой окрестности точки х0 выполняется неравенство ( х) ( х0).
Точка х1 называется точкой максимума функции ( х), если в некоторой окрестности точки х1 выполняется неравенство ( х) ( х1).
Значение функции в точках х0 и х1 называются соответственно
максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.

Необходимое и достаточное условия экстремума
Теорема (необходимое условие экстремума) Для того чтобы функция у = ( х) имела экстремум в точке х0, необходимо, чтобы ее производная в
этой точке равнялась нулю ( ( х0) = 0) или не существовала.
Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются стационарными. Обращаем внимание на то, что эти точки должны входить в область определения функции.
Теорема (достаточное условие существования экстремума). Если при переходе через точку х0 производная дифференцируемой функции меняет свой знак с плюса на минус, то точка х0 есть точка максимума функции у = ( х), а если с минуса на плюс, то - точка минимума.

Схема исследования функции на экстремум
Найти производную у = ( х).
Найти стационарные точки функции, в которых производная ( х) = 0 или не существует.
Исследовать знак производной слева и справа от каждой стационарной точки и сделать вывод о наличии экстремумов функции.
Найти экстремумы (экстремальные значения) функции.

Выпуклость функции. Точки перегиба.
Функция у = ( х) называется выпуклой вниз на промежутке Х, если для любых двух значений х1, х2 Х выполняется неравенство:
x x |
|
|
f (x ) f (x ) |
|
|||
f |
1 |
2 |
|
|
1 |
2 |
. |
|
2 |
|
2 |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Функция у = ( х) называется выпуклой вверх на промежутке Х, если для любых двух значений х1, х2 Х выполняется неравенство:
|
|
|
|
|
f (x ) f (x ) |
|
|
x x |
|
|
|
||||
f |
1 |
2 |
|
|
1 |
2 |
. |
|
2 |
|
2 |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|

Теорема. Функция выпукла вниз (вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).
Теорема (достаточное условие выпуклости функции вниз(вверх)). Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке.

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.
Теорема (необходимое условие перегиба). Вторая производная дважды дифференцируемой функции в точке перегиба х0 равна нулю, т.е. ( х) = 0.
Теорема (достаточное условие перегиба) Если вторая производная
дважды дифференцируемой функции при переходе через некоторую точку х0 меняет свой знак, то х0 есть точка перегиба.
Следует отметить, что если стационарная точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.
