Асимптоты графика функции

Асимптотой графика функции у = ( х) называется прямая, обладающая следующим свойством, что расстояние от переменной точки на графике до этой прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.

Теорема 1. Пусть функция у = ( х) определена в некоторой окрестности точки х0 (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х х0 – 0 (слева) или при х х0 + 0 (справа) – равен бесконечности, тогда прямая при х = х0 является вертикальной асимптотой графика функции у = ( х).

Замечание. Вертикальные асимптоты следует искать в точках разрыва функции у = ( х) или на концах ее области определения (а, b) если а и b - конечные числа.

Теорема 2. Пусть функция у = (х) определена при достаточно больших х и существует конечный предел функции при х и он равен числу b.

Тогда прямая у = b есть горизонтальная асимптота графика функции у

= ( х).

Замечание. Если конечен лишь один из пределов слева или справа, то функция имеет лишь левостороннюю или правостороннюю асимптоту.

Теорема 3. Пусть функция у = ( х) определена при достаточно больших х и существует конечные пределы

		f (x)
	lim		k и	lim [ f (x) kx] b.
		x
	x			x

Тогда прямая у = kx + b является наклонной асимптотой.

Тема: Производная и дифференциал.

Основные теоремы о дифференцируемых функциях.

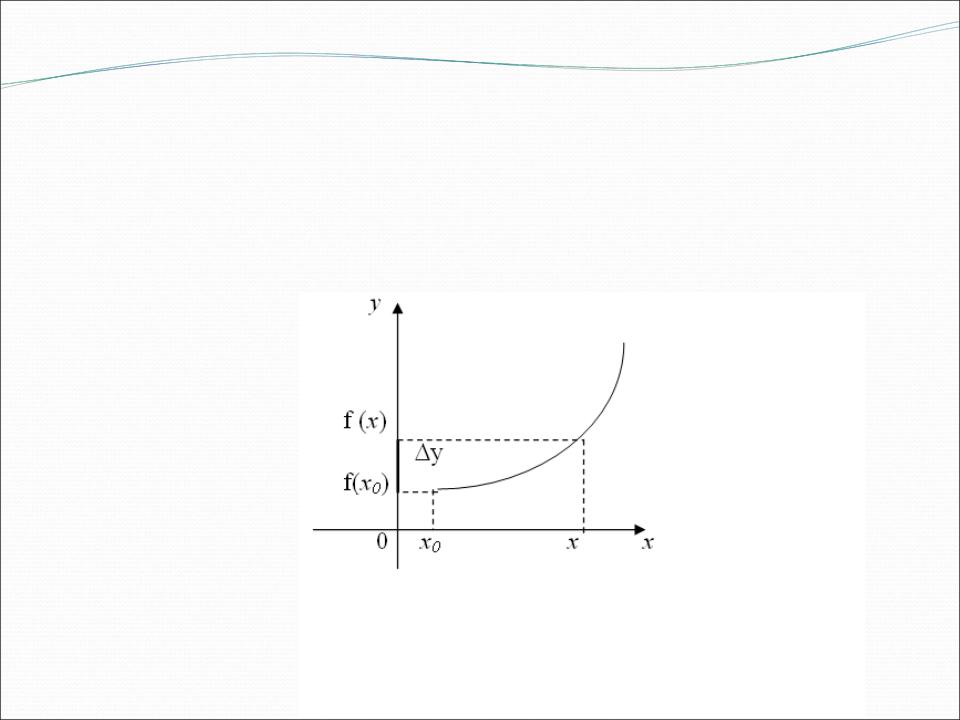
приращение аргумента и функции

Пусть дана функция у = (х). Рассмотрим два значения ее аргумента:

исходное х0 и новое х.

Разность х = х - х0 называется приращением аргумента х в точке х0.

Разность у = у – у0 = (х)- (х0) называется приращением функции у = (х) в точке х0 .

Определение производной

Пусть функция у = (х) определена на промежутке Х. Возьмем точку х Х. Дадим значению х приращение х 0, тогда функция получит приращение у = ( х+ х ) - ( х ).

Производной функции у = (х) называется предел отношения

приращения функции у к приращению аргумента х при стремлениих к нулю.

Если функция в точке х0 имеет конечную производную, то функция называется дифференцируемой в этой точке.

Производная функции	у = (х) в точке х0 является значением
функции ( х) в точке х0.

Функция дифференцируемая во всех точках промежутка Х, называется

дифференцируемой на этом промежутке.

Геометрический смысл производной

Производная f ( x0 ) есть угловой коэффициент касательной (тангенс угла наклона касательной), проведенной к кривой y=f(x) в точке х0.

Уравнение касательной к кривой y=f(x) имеет вид: y f ( x0 ) f ( x0 )( x x0 ).

Правила дифференцирования

Производная постоянной равна нулю, т.е. С =0.

Производная аргумента равна 1, т.е. х =1

Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е. (u + v) = u + v .

Производная произведения двух дифференцируемых функций вычисляется по формуле: (u v) = u v + u v .

Следствие. Постоянный множитель можно выносить за знак производной: (Сu) = Cu .

Производная частного двух дифференцируемых функций может быть найдена по формуле:

u '		u'v v'u	.
v		v2

Производная сложной функции

Теорема. Если у = f(u) и u = (x) – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна

произведению данной функции по промежуточному аргументу и

умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е у = (u)u .

Пример.

Таблица производных

№ Функция у

	1	C
	2	x
	3	1
		u
	4	eu
	5	au

Производная у

0

1

1 u u2

eu u

au ln a u

№ Функция у

9 sin u

10 cos u

11 tg u

12 ctg u

13 arcsin u

Производна я у

cos u u

sin u u

12 u cos u

	1	u
sin2 u
1				u
1 u2