моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

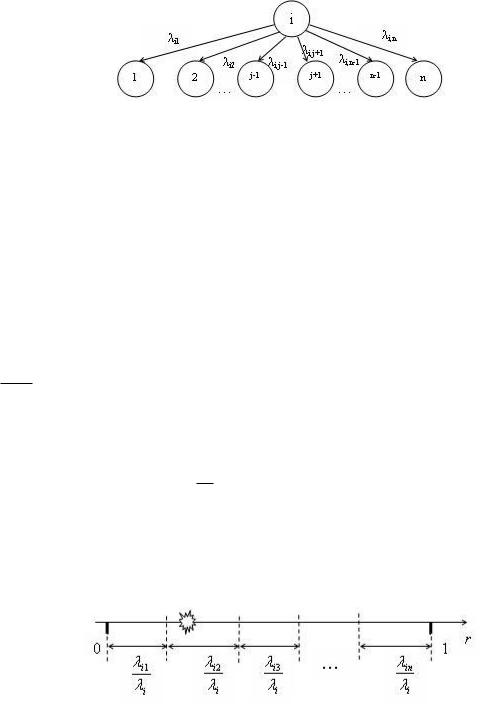
предпочтительнее использовать другой способ, в котором учитываются реальные законы перехода и сразу определять время перехода.

Рассмотрим переходы из i - го состояния (рис. 2.3.2).

Рис. 2.3.2 Граф переходов из i - го состояния

Возникает вопрос: как по интенсивностям разыграть состояние, в которое произойдет переход?

При разрешении поставленного вопроса возникает необходимость решения двух задач:

-определение времени перехода,

-определение состояния, в которое переходит система из текущего состояния (i -е состояние).

При экспоненциальном распределении времени выхода из текущего состояния имеем: Pi (t) e i t . Отсюда время перехода в другое состояние определяется по формуле:

t ln(r) , где r – число, сгенерированное ДСЧ.

i

Для решения второй задачи диапазон ДСЧ (0…1) разбивается на отрезки, пропорциональные вероятности перехода в другое состояние (как для марковских цепей).

Значения этих вероятностей равны ij . Очевидно, что сумма этих вероятностей по всем j

i

равна единице.

Теперь остается выбрать r и тем самым определить, в какое состояние перейдет система. Например, значение r попало во второй интервал (рис.2.3.4), следовательно, следующее состояние, в которое перейдет система, будет второе состояние.

Рис. 2.3.4 Моделирование перехода из i-го состояние

Возможен и другой вариант моделирования марковского процесса. Для каждого возможного перехода разыгрываются времена перехода:

t	ln(r1 )	,t			ln(r2 )	,...,t			ln(rn )
			2				n
1	i1				i 2				in

и выбирается наименьшее из них, т.е. если tj – min, то t = tj и система перейдет в j-е состояние.

91

Такой вариант не требует расчета вероятностей переходов и разбиения диапазона ДСЧ на интервалы, но приводит к большому числу обращений к ДСЧ.

Моделирование систем массового обслуживания

В теме № 1 рассматривались системы, для которых удается описать результаты исследования в аналитическом виде. Однако многие реальные системы не поддаются такому решению. В этих условиях для оценки качества функционирования систем обслуживания широко используют метод статистических испытаний.

Основой решения задачи исследования функционирования СМО в реальных условиях является статистическое моделирование входящего потока требований и процесса их обслуживания (исходящего потока требований).

Для решения задачи статистического моделирования функционирования СМО должны быть заданы следующие исходные данные:

-описание СМО (тип, параметры, критерии эффективности работы системы);

-параметры закона распределения периодичности поступлений требований в систему;

-параметры закона распределения времени пребывания требования в очереди (для СМО с ожиданием);

-параметры закона распределения времени обслуживания требований в системе.

Суть математического моделирования систем массового обслуживания заключается в следующем.

Время функционирования системы разделяется на достаточно большое количество подинтервалов (единиц времени, в течение которых не может возникнуть более одной заявки или завершиться выполнение более одной заявки).

Для каждого такого подинтервала:

-последовательно моделируется факт появления новой заявки (да/нет). Вырабатывают равномерно распределенное случайное число. Равномерно распределенные случайные числа преобразуют в величины с заданным законом распределения: интервал времени между поступлениями требований в систему; время ухода заявки из очереди (для СМО с ограниченной длиной очереди); длительность времени обслуживания требования каналами;

-проверяется наличие свободного канала (закончено ли обслуживание какой-то заявки) и загрузка его заявкой из очереди,

-проверяется наличие мест в очереди с последующим выводом (принять в очередь/отказать в обслуживании) и т.д.

Фиксируется число отказов, время ожидания заявок в очереди и в системе вообще, число заявок в очереди в каждый момент и другие значения.

Рассчитываются вероятность отказа, распределение времени ожидания, среднее время, вероятность простоя каналов и т.п.

92

Разовое моделирование многократно повторяется. В итоге показатели качества функционирования системы определяется путем обработки накопленных результатов моделирования методами математической статистики.

Для решения подобной задачи приходится использовать компьютер со встроенным или программным датчиком псевдослучайных чисел с равномерным законом распределения в интервале от 0 до 1. В процессе моделирования возникает необходимость генерации случайных чисел с требуемым законом распределения (методы решения такой задачи были рассмотрены выше).

Раздел 3. Построение математических моделей по экспериментальным данным

Теоретические занятия (лекции) – 6 часов.

Лекция 7. Методы исследования математических моделей систем и процессов

Цель лекции: ознакомить обучающихся с общей методикой и особенностями оценивания параметров моделей, которые заданы распределением случайных величин.

Введение

Как правило, математические модели сложных систем получаются не сразу. Например, точность модели работы системы автоматического регулирования, полученной расчетным путем, составляет примерно 50-60%. На практике строят начальную модель, которую постепенно уточняют до достижения ею основных требований. Основной информацией для уточнения или построения различного рода моделей являются опытные данные.

Использованием экспериментальных данных для уточнения или построения моделей занимаются два направления: математическая статистика и теория автоматического управления.

Вматематической статистике этому посвящены следующие разделы:

оценивание параметров распределений;

корреляционный анализ;

регрессионный анализ;

дисперсионный анализ;

анализ временных рядов;

планирование эксперимента.

Оценивание параметров распределения

Распределение случайных величин является моделями. Например, распределение времени отказа системы используют как модель надежности системы. Очень часто возникают задачи уточнения предполагаемых распределений. Уточнить можно только опытным путем, при котором получают оценки требуемых показателей.

93

Известны и используют два подхода к оцениванию: точечное и интервальное.

При точечном оценивании находят наилучшую оценку показателя и указывают погрешность оценки (дисперсию).

При интервальном оценивании определяют интервал, который накроет истинное значение параметра с заданной (доверительной) вероятностью.

При точечном оценивании стремятся получить такие оценки, которые будут удовлетворять трѐм свойствам:

-несмещенности;

-состоятельности;

-эффективности.

Оценка является несмещенной, если ее математическое ожидание равно истинному

значению оцениваемого параметра, т.е. ˆ .

M Q Q

Оценка называется состоятельной, если она сходится по вероятности к истинному значению, т.е. стремится к нему, когда объем выборки стремится к бесконечности.

Оценка эффективна, если она имеет минимальную дисперсию из всех оценок. Известны следующие методы оценивания:

1.Метод сравнения

2.Метод максимального правдоподобия

3.Байесовский метод.

Метод сравнения

Заключается в приравнивании опытных (выборочных) и теоретических величин, имеющих одинаковый физический смысл. Например, число отказов в интервале, вероятность событий, суммарная наработка.

Приравнивание дает уравнение (или систему уравнений), а параметры определяются как решение этих уравнений.

В литературе этот метод называется как метод моментов, в котором в качестве сравниваемых величин выступают начальные или центральные моменты.

Для случайной величины X теоретический начальный момент k-го порядка: vK M x K - матожидание от k-той степени случайной величины.

Если x1 ,x2 …xN – реализация выборки, т.е. опытные (выборочные) значения случайной величины, то выборочный начальный момент k-го порядка равен:

1 N

v N xiK .

i 1

Теоретический центральный момент k-го порядка равен:

K M x M x K ,

Выборочный центральный момент k-го порядка равен:

94

				1		N			1	N
			K			xi	x K	, где x		xi .
				N 1					N
						i 1				i 1
	N-1 -			число степеней свободы (одна затрачена на определение x ).

Было N независимых результатов в выборке, после определения x один результат может быть вычислен по другим результатам и по x . Один элемент выборки использован

на определение x		и ―пропал‖. Оценки при делении на N-1 должны получится более
точными. Покажем это на примере.
Пример.
Пусть случайная величина Х может принимать значения 0, 1, 2 и 3, причем
вероятности событий равенства Х значениям известны.
Закон распределения величины X задан в виде ряда распределения:
Значение X		0		1		2		3
Вероятность		0,1		0,4		0,4		0,1
Определим математическое ожидание и дисперсию случайной величины:
M x 0 0,1 1 0,4 2 0,4 3 0,1 1,5
~
D x 0,1 0 1,52 0,4 1 1,52 0,4				2 1,52 0,1 3 1,5 2		0,65

~

Допустим, что распределение случайной величины неизвестно. В этом случае можно оценить дисперсию (определить приближенное значение – оценку), выбрав Х определенное число раз (объем выборки N).

Пусть N = 2; х1 = 1; х2 = 2.

х 1,5
D x		1		2 1,5 2 1 1,5 2				0,5
	2	1
~								.
При делении не на					1		,	а на	1	получили бы 0,25, что дальше от истинного
					N 1				N

значения дисперсии, которое равно 0,65.

Оценим методом моментов параметры гамма распределения

fx k xk 1 x ,

Гk

где α и k – параметры, Г(k) – гамма-функция.

Известно, что теоретические начальные моменты первого и второго порядков

соответственно равны v		k	, v			k k 1		. Из опытных значений (выборки) можно
				2
1						2

получить выборочные начальные моменты v1 ,v2 . Приравнивая теоретические начальные моменты и выборочные, получим систему из двух уравнений. В результате решения этой

95

системы относительно искомых параметров можно получить выражения для расчета их оценок:

			v12				v1 .
k				,
	v	2	v 2		v	2	v 2
			1				1

Наиболее просто метод моментов выглядит при оценивании самих моментов. Выборочное оценивание моментов и является их оценкой.

Одними из основных характеристик распределения случайной величины являются математическое ожидание и дисперсия. Согласно методу моментов их оценки равны выборочным начальному моменту 1 порядка и центральному моменту 2 порядка.

Если a M x , 2 M x x 2 , то их оценки соответственно будут равны

			1	N		2		1		N
										2
	a			xi	x ,					xi x .
			N					N 1
				i 1						i 1

Можно показать, что эти оценки несмещены и состоятельны. Действительно

1

N

1

M a

M xi

N a a

N

N

i 1

~

, следовательно, оценка несмещена.

a

1

N

N

2

2

D a

D xi

,

N

2

N

2

N

i 1

т.е. a стремится к a при N , значит оценка состоятельна.

y C1 X1 ... Cn X n

D y C 2 D X ... C 2 D X

напоминание

1

1

n

n

Покажем несмещенность оценки для дисперсии:

2

1

N

2

1

N

2

N

2

xi a

x a

xi

a

2 x

a xi

a N x a

N

1

N 1

i 1

i 1

i 1

1

N

2

2

xi

a

N

x a

N 1

i 1

Математическое ожидание оценки

1

N

1

2

2

2

2

2

M

M (xi a)

N M x a

N

,

N 1

N 1

i 1

2

2

N

т.е. оно совпало с истинным значением, следовательно, оценка несмещена. В математической статистике доказано, что оценка дисперсии состоятельна.

96

Также доказано, что при нормальном распределении случайной величины Х оценки математического ожидания и дисперсии эффективны.

Пример применения метода сравнения.

Пусть требуется оценить	ˆ	- среднее время безотказной работы при плане [NUT].
	Т с

Результатом испытаний является m – число отказов и закон распределения времени отказов экспоненциальный.

T

Теоретическая вероятность безотказной работы P(T ) e Tc .

Выборочная вероятность безотказной работы 1 mN .

Приравняем теоретическую и выборочную вероятности и получим искомую оценку среднего времени безотказной работы:

Т

m

Тˆ

1

с

N

T

m

n 1

ˆ

T

N

c

ˆ

T

Tc

m

n 1

N

Метод максимального правдоподобия

По методу максимального правдоподобия (ММП) оценки получаются из условия максимизации функции правдоподобия (вероятности или плотности результата эксперимента).

Обозначается функция правдоподобия следующим образом: для дискретных случайных величин –

			N
P результат, P x1 , x2 ...xn , П P xi , L результат, ,
			i 1
для непрерывных случайных величин –
	N
P x1 ,...,xn , x N	П f xi , L результат ,
	i 1
f - плотность распределения.
Таким образом, можно записать:
	N
	П P xi , для дискретных СВ,
L результат i 1			.
	N	f xi	, для непрерывных СВ.
	П
i 1

97

Максимум функции правдоподобия можно найти, приравняв ее производную к

nL

нулю. Иногда удобнее максимум находить из уравнения 0 , причем точки

Q

экстремума в двух случаях получаются одни и те же в виду монотонности функции логарифма.

Пример применения метода максимального правдоподобия.

Пусть требуется оценить ˆ - среднее время безотказной работы при плане [NUN].

Т с

Результатом испытаний являются t1, t2,…tN - моменты отказов (наработка) каждого объекта. Закон распределения времени отказов экспоненциальный.

Запишем произведение плотностей для непрерывной СВ.

L t ,...,t

,T

1

t

1

t2

1

tN

1

ti

Tс

Tс

Tс

Tс ,

1

N с

1

Т

T

Т

Т N

с

с

с

с

далее запишем логарифмическую функцию правдоподобия, найдем ее производную и определим искомую оценку

n L N nTср ti

Tср

n L				N			ti
T				Т	ср		T 2
	ср						ср
N		ti					ˆ		1	N
ˆ		ˆ 2			Tср					ti .
									N i 1
T		Т	ср
ср

В качестве другого примера оценим вероятность наступления события m раз в N случаях.

Функция правдоподобия в соответствии с биномиальным законом распределения имеет следующий вид:

L m,Р CNm Pm 1 P N m .

Согласно методу максимального правдоподобия получим искомую оценку

n L m,P n C m m n P N m n 1 P
L m,P							N
					m		N m
	P				P		1 P
m		N m						m
				P
P		1	P					N

Оценим точность полученной оценки, т.е. определим ее дисперсию.

Число m можно представить суммой случайных величин, принимающих значение 0

или 1: m = z1 + z2 +…+ zN, причем

1 при успехе

Zi 0 в противном случае .

98

Так как Z независимы, то

M Z 0 1 P 1 P P;				M P N P P оценка не смещена
						N
D Z 0 P 2 1 P 1 P 2 P P 1 P
			P 1 P
D P	1	N D Z			0 при N , оценка состоятельна.
	N 2
			N

Исследуем, является ли полученная оценка эффективной. Для этого используем неравенство Рао-Крамера, определяющее нижнюю границу выборочной дисперсии несмещенной оценки:

	1
D P		,
	I N (P)
			2	ln L(m, P)			и является количеством информации об оцениваемом
где I N (P) M				P	2

параметре, которая содержится в выборке. Очевидно, что

2 Ln(m, N )

m

N m

.

P2

P2

(1 P)2

Тогда, учитывая, что M m NP получим

2 Ln(m, N )

NP

N NP

N (1 P) NP

N

M

.

P

2

P

2

(1

P)

2

P(1 P)

P(1

P)

В итоге получили количество информации

I N (P)

N

.

P(1

P)

Следовательно, неравенство Рао-Крамера будет иметь следующий вид:

P(1 P)

D P . N

Таким образом, нижняя граница выборочной дисперсии, определяемая неравенством, совпадает с ранее полученным выражением для дисперсии искомой оценки, что дает возможность сделать вывод об эффективности оценки m/N.

Байесовский метод

Свое начало байесовский подход к оцениванию параметров берет с работы Томаса Байеса, впервые опубликованной в 1763 году. В последнее время развитие байесовской теории связано с появлением работ Де Гроота, Райфы, Зельнера. В нашей стране идеи этой теории нашли поддержку в работах Савчука В.П., Щербинина А.Ф., Ивченко Б.П. и других.

В настоящее время теория субъективной вероятности, на которой построен байесовский подход к оцениванию параметров, широко применяется в системах искусственного интеллекта в целях учета различного рода неопределенностей.

99

Современные сторонники байесовской теории считают, что байесовский подход не противоречит классической теории статистического анализа. Классическая теория оставляет задачу выбора на усмотрение исследователя, не используя его знаний на заключительной стадии оценивания. Байесовская теория формализует этот этап, и может, поэтому рассматриваться как формальное завершение классической теории.

Исходной информацией для получения байесовской оценки являются:

1)априорное распределение исследуемого параметра;

2)результаты испытаний;

3)функция потерь.

Методической основой процесса перехода от дополнительной (априорной) информации (АИ), представленной в виде априорного распределения, к апостериорной информации путем добавления экспериментальных данных является теорема Байеса.

На основе априорного распределения f А ( р) и экспериментальных данных по теореме Байеса определяется апостериорное распределение:

f ( р)	f A	( р) вер( рез / р)	,
	1
	f A ( р) вер( рез / )dр
	0

где вер(рез/р) – вероятность результата испытания при условии, что параметр равен р.

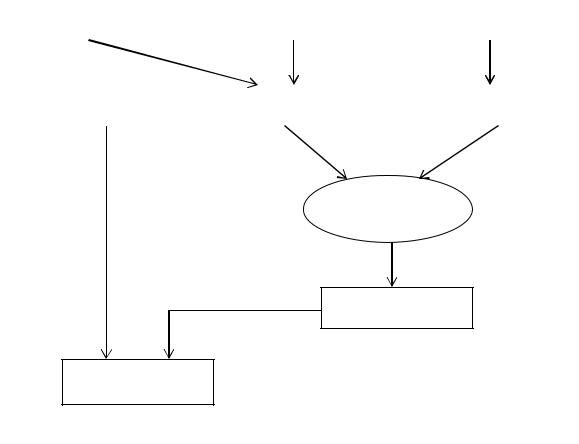
Из апостериорного распределения в зависимости от вида функции потерь определяется байесовская оценка. Этот процесс можно представить в виде уточнения АИ результатами эксперимента (рис. 7.1).

Данные предыдущих		Неформальный опыт		Новые
исследований		исследователя		экспериментальные

Вид функции потерь		Априорное		Функция правдоподобия
		распределение

ТЕОРЕМА

БАЙЕСА

Апостериорное

распределение

Получение байесовской оценки

Рис. 7.1 Процесс уточнения априорной100 информации