моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

Выбор априорного распределения

Априорное распределение представляет собой дополнительную, субъективную информацию, которой необходимо задаться для получения байесовской оценки.

Существует несколько способов, позволяющих определить вид априорного распределения.

Рассмотрим способ, основная идея которого заключается в том, что для обеспечения гарантии достоверности АИ выбирают такое априорное распределение, которое будет иметь наибольшее рассеивание при имеющихся предварительных данных. В качестве меры рассеивания удобно выбрать энтропию распределения:

H f (x) ln( f (x))dx .

Решение задачи сводится к определению функции f(x), подчиненной некоторым уравнениям связи, энтропия которой максимальна. АИ используется при составлении уравнений связи.

Предположим, что АИ задана в виде интервала [xH,xB]. Определим вид функции f(x), согласующийся с опытными данными и обладающим наибольшим рассеиванием.

При наличии подобной АИ можно составить одно уравнение связи:

X B f (x)dx 1 .

X H

Тогда функция правдоподобия, выраженная через множители Лагранжа, будет иметь следующий вид:

L f (x) ln f (x) 1 f (x) , где θ1 – неопределенный множитель Лагранжа.

	Дифференцируя по f(x) получим ln f (x) 1				0 , откуда		f (x) e 1 1 .
			1
	Подставив последний результат в уравнение связи, получим
	X B	X B						1
		e 1 1 dx e 1 1 x |	e 1 1 ( X B X H ) 1, тогда e	1 1 f (x)					.
						X B		X H
	X H	X H

Таким образом, при представлении АИ в виде интервала, в качестве априорного распределения следует выбирать равномерное распределение.

При представлении АИ в виде оценки неизвестного параметра и ее дисперсии определить вид априорного распределения можно на основе принципа сопряженности. Его суть в следующем.

В общем случае по теореме Байеса любое априорное распределение может быть использовано с любой функцией правдоподобия. В практических случаях обычно используют априорное распределение специальных форм, приводящих к простым оценкам. Для распределения результатов эксперимента можно подобрать такое семейство априорных распределений, что и апостериорные распределения будут принадлежать тому

101

же семейству. Такое семейство называется сопряженным относительно распределения результатов эксперимента.

При оценивании вероятности наступления события m раз в N случаях распределение результатов является биномиальным. Известно, что для биномиального распределения сопряженным распределением является бета-распределение, т.е. в таком случае и апостериорное распределение будет также бета-распределением. Таким образом, для рассматриваемого варианта представления АИ в качестве априорного распределения целесообразно принять бета-распределение:

			р a 1	(1 р)b 1
f	A	( р)			,
			B(a, b)

где B(a,b) - бета-функция, a, b – параметры бета-распределения.

При определении параметров a и b обычно полагают априорную оценку математическим ожиданием априорного распределения, а ее дисперсию – дисперсией априорного распределения:

			рˆ А			a
						a b
								,
							a b
				2
				A		(a b)2 (a b 1)
где	рˆ	A	, 2			- априорная оценка вероятности и ее дисперсия соответственно.
					A

В результате решения системы можно получить:

aрˆ A ( рˆ A (1 рˆ A )

A2

1) ,	b a	(1 рˆ A )	.
		рˆ A

Логично предположить, что априорную оценку можно считать и наиболее вероятным значением неизвестного параметра, т.е. модой априорного распределения:

	рˆ А	a 1	. В этом случае решение системы уравнений возможно лишь численными
		a b 2

методами.

В случае, когда дисперсия априорной оценки неизвестна, параметры априорного распределения можно определить либо с помощью рациональных степеней уверенности исследователя в качестве АИ, либо с помощью субъективных уровней доверия к ней. Сущность способа использования рациональных степеней уверенности заключается в применении такого априорного распределения, которое гарантирует, что потери будут не больше ожидаемых.

Суть способа субъективных уровней доверия заключается в том, что для определения параметров априорного распределения вводится байесовская информация, которая содержится в априорном распределении об оцениваемом параметре. Определяется она также как и информация Фишера. Исследователь, используя свои знания и опыт, а также мнения экспертов, задает весовую значимость априорной информации по отношению к опытной:

102

		I Б	( р)
	S	a,b		,
		I N ( р)

где I aБ,b ( р) - байесовская информация,

I N ( р) - информация Фишера.

Значение S показывает, насколько исследователь доверяет АИ по отношению к опытным данным.

Значения параметров априорного бета-распределения можно определить из системы уравнений:

	a		рˆ
				А		.
a b
I Б		( рˆ ) S I			N	( рˆ )
	a,b

В результате ее решения получим: a рˆ A рˆ A 1 рˆ A I N ( р)S 1 ,

b a 1 рˆ A .

рˆ A

Отметим, что выбор вида априорного распределения должен основываться на разумном сочетании субъективных знаний и объективных данных. Существует опасность злоупотребления неформальным знанием, что в итоге приведет к ошибочному выбору априорного распределения.

Определение апостериорного распределения

Выше было отмечено, что для определения апостериорного распределения используется формула Байеса, в которую входят априорное распределение и вероятность

результата испытаний.
При биномиальной схеме эксперимента вероятность результата	равна
p(m, N ) (1 p)m p N m .

Получим апостериорные распределения при рассмотренных выше априорных распределениях.

А) априорная информация выражена в виде априорного бета-распределения. Применив теорему Байеса, получим апостериорное распределение, которое тоже

является бета-распределением:

f ( р)	р a N m 1 (1 р)b m 1	.
	1
	р a N m 1 (1 р)b m 1 dр
	0

Для примера на рисунке 7.2 показаны априорное бета-распределение с параметрами a=3, b=5 (что соответствует рˆ А =0,4) и апостериорное распределение при результатах испытаний m=3, N=4.

Б) априорная информация выражена в виде равномерного распределения.

103

Апостериорное распределение в этом случае будет иметь следующий вид:

f ( р)	(1 р)m р N m
		,
	рB
	(1 р) m р N m dр
	рH

где рН , рВ - нижняя и верхняя границы априорного распределения соответственно.

Для примера, на рисунке 7.3 показаны априорное равномерное распределение с границами [0.2;0.7], и апостериорное распределение при результатах испытаний m=1,

N=4.

Отличие апостериорного распределения от априорного в обоих случаях вызвано результатом испытаний, и отличие тем больше, чем сильнее отличается экспериментальная оценка от априорной.

2.935107	3
	2
f a ( )
f( )
	1
0	0
	0	0. 2	0. 4		0. 6	0. 8	1
	0						1
	Рис. 7.2 Априорное и апостериорное бета-распределения

2.98 566 9	4
f a( )
	2
f( )
0	0
	0	0.2	0.4	0.6	0.8	1
	0					1
	Рис. 7.3 Равномерное априорное и апостериорное распределения

Пример. Расчет байесовской оценки при биномиальной схеме испытаний

При проведении статистического эксперимента неизбежны потери, возникающие вследствие замены истинного значения параметра его оценкой, выражающиеся функцией потерь ( рˆ, р) . В зависимости от характера потерь исследователь может обосновать вид функции потерь. Рассмотрим различные ее виды и для каждой функции запишем лучшую (которая минимизирует функцию потерь) байесовскую оценку.

Оценки получим в случае, когда в качестве априорного распределения выбрано бета-распределение.

104

В случае равномерного априорного распределения байесовские оценки для будут определятся аналогично, т.е. как медиана, математическое ожидание и мода

апостериорного распределения.
В теории оценивания		широко используется функция потерь	вида:
( р, рˆ ) C( р) рˆ р k ,	где C( р)	- функция от неизвестного параметра,	которая

предполагается положительной и конечной.

При k=1 функция потерь линейна, при ней лучшей байесовской оценкой является медиана апостериорного распределения, определяемая из уравнения:

F ( рˆ	Ме )	B	рМе (a N m, b m)			1	,
			Б
	Б	B(a N m, b m)				2
				p Ме
				Б
где BpБМе (a N m,b m)				(1 p)a N m 1 pb m 1dp - неполная бета-функция.
				0

При k=2 функция потерь является квадратичной. Известно, что при квадратичной функции потерь лучшая байесовская оценка определяется как математическое ожидание апостериорного распределения:

1

p a N m (1 p)b m 1dp

pˆ БМО 10

p a N m 1 (1 p)b m 1dp

0

B(a N m 1, b m) . B(a N m, b m)

Получим аналитическое выражение этой оценки. Для этого выразим бета-функцию через гамму-функции:

B(a N m 1,b m) (a N m 1) (b m) ,(a b N 1)

Подставив (3.8) в (3.7), с учетом свойств гамма-функции, получим байесовскую оценку:

pˆ	МО		a N m	.
	Б
			a b N

В теории оценивания также используется квадратичная функция потерь относительной ошибки вида:

		рˆ р		2
( рˆ	, р)			,
		р

для которой лучшая байесовская оценка равна

	1	f ( р)
		р	dр
рˆ БОт	0			.
	1	f ( р)
		р 2	dр
	0

Проведя аналогичные преобразования можно получить:

105

pˆ	От	a N m 2	.
	Б	a b N 2

При отсутствии информации о виде функции потерь логично выбрать в качестве байесовской оценки моду (наиболее вероятное значение) апостериорного распределения:

a 1 N m

pˆ БМода a b N 2 .

Лекция 8. Обработка результатов имитационного эксперимента

В лекции рассматриваются методы решения задач аппроксимации опытных данных. Дается определение испытаний, отмечается место эксперимента в общей структуре классификации испытаний. Приводится определение регрессионной модели, раскрывается ее общий вид. Подробное внимание уделяется назначению базисных функций, перечисляются их возможные аналитические выражения. Описывается метод наименьших квадратов.

Обработка массива данных

Первичная обработка исходных данных и построение гистограммы

При большом числе наблюдений простая статистическая совокупность становится неудобной формой записи статистического материала, ввиду громоздкости и малой наглядности. Для большей компактности и наглядности статистический материал подвергается дополнительной обработке, в частности строится статистический ряд.

Статистический ряд представляется графически в виде гистограммы. По оси абсцисс гистограммы откладываются интервалы, на каждом из которых, как на основании, строится прямоугольник, высота которого пропорциональна (в выбранном масштабе) соответствующей частоте попадания конкретного значения в интервал.

Перед построением гистограммы данные сортируют (по возрастанию), определяют минимальное xmin и максимальное xmax значения, а также размах вариационного ряда

(xmax- xmin).

Для построения гистограммы интервал изменения данных нужно разбить на участки одинаковой длины. С одной стороны, число таких участков должно быть как можно больше, а с другой стороны, в каждый из этих участков должно попадать как можно больше значений xi.

Компромисс между этими требованиями приводит к тому, что обычно выбирают число интервалов k для построения гистограммы как ближайшее целое к n . Используют и другие подходы к определению числа интервалов. Например, известна формула Стэрджесса: k 1 3.322 lg( n) .

Расчет статистических параметров распределения

Точечные оценки

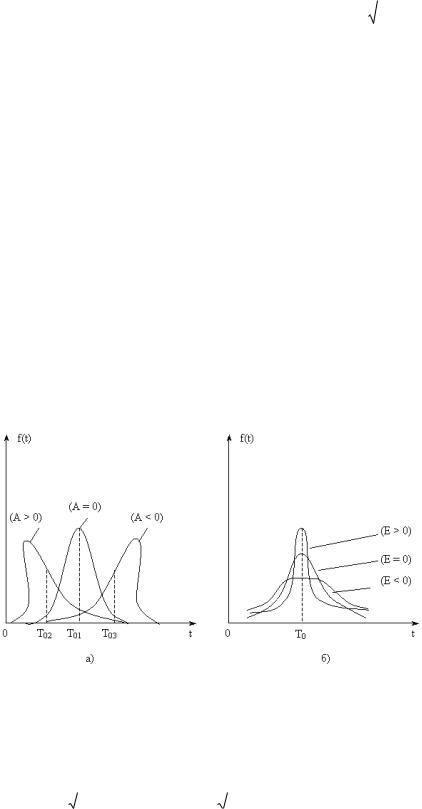
Расчет статистических параметров распределения (точечных оценок) проводят по следующим формулам:

106

~

~

1

n

математического ожидания mx :

mx

xi

n

i 1

~

~

1

n

~

2

дисперсии

Dx :

Dx

xi

mx

n 1

i 1

~

~

~

среднеквадратичного отклонения x :

x

Dx

~

~

1

n

~

3

асимметрии ax

:

ax

xi mx

n

~3

1 x

i 1

~

1

n

~

4

эксцесса ex

: ex

xi mx

3

n

~ 4

1 x

i 1

Последние две характеристики используются для выбора аппроксимирующей функции.

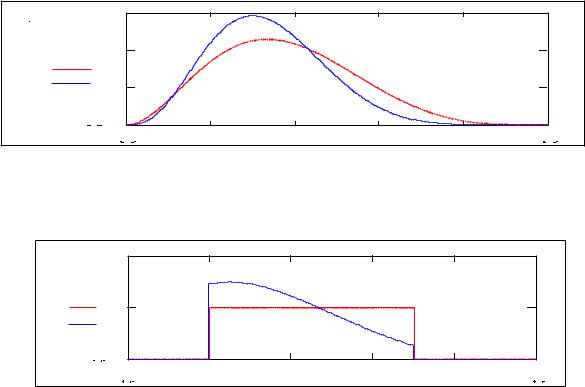
Коэффициент асимметрии является характеристикой «скошенности» распределения, например, если распределение симметрично относительно математического ожидания, то

~	= 0.
ax
	На рис. 8.1,а распределение f2(t) имеет положительную асимметрию		~	> 0, а f3(t) –
			ax
	~	< 0 (на рисунке асимметрия обозначена как A).
отрицательную ax
	Эксцесс характеризует «крутость» (остро или плосковершинность) распределения.
		~
Для нормального распределения ex = 0.
	Кривые f(t),	более островершинные по сравнению с нормальной, имеют			~
					ex > 0, а

наоборот – более плосковершинные, ~ < 0 (рис.8.1,б, эксцесс обозначен как E). ex

Рис. 8.1 Влияние асимметрии и эксцесса

Доверительные оценки параметров распределения (интервальные оценки)

Доверительный интервал для математического ожидания mx имеет вид

~

p f

~

p f

xt

xt

~

1

~

1

2

2

mx

mx mx

,

n

n

107

где tp(f) квантиль t-распределения Стьюдента, соответствующий уровню значимости p (в зависимости от значения уровня значимости квантиль берется из таблиц).

Доверительный интервал для дисперсии Dx находится по формуле

	~								~
fDx				D			fDx			,
2		f			x		2		f
1	p							p
	2						2

где p2(f) квантиль 2-распределения Пирсона, соответствующий уровню значимости p (берется из таблиц).

Для нахождения доверительного интервала для асимметрии ax и эксцесса ex используется неравенство Чебышѐва:

~

Da

~

Da

~

De

~

De

ax

ax ax

; ex

ex ex

,

p

p

p

p

где Da, De дисперсии выборочных асимметрии и эксцесса:

	D	6 n 1		; D	24n n 2 n 3	.
		n 1 n 3			n 1 2 n 3 n 5
	a			e

Подбор теоретического распределения и его параметров

Выбор закона распределения состоит в подборе аналитической функции наилучшим образом аппроксимирующей эмпирические функции.

Выбор, в значительной мере, процедура неопределенная и во многом субъективная, при этом многое зависит от априорных знаний об объекте и его свойствах, условиях работы и т.д.

Подбор теоретического распределения состоит из следующих этапов:

1.Подбор вида распределения (т.е. закона).

2.Подбор параметров распределения (т.е. чисел, входящих в выражение для функции и плотности распределения).

3.Проверка правильности подбора.

Таким образом, сначала подбирают вид теоретического распределения и его параметры, затем проверяют правильность подбора с помощью критериев согласия, например, Колмогорова или Пирсона.

Закон теоретического распределения подбирается исходя из вида гистограммы. Вначале обычно делается предположение, что теоретическое распределение может

быть одного из нескольких видов, например, наиболее распространенными на практике законами распределения являются:

1.Нормальное.

2.Показательное (экспоненциальное).

3.Равномерное.

4.Распределение Рэлея.

Затем выбирается наиболее подходящее из них.

108

Параметры, входящие в выражение для функции и плотности теоретического распределения, находятся исходя из принципа максимума правдоподобия: так, чтобы вычисленные по этим параметрам математическое ожидание (для 1-параметричеких законов) или математическое ожидание и дисперсия (для 2-параметрических законов) совпали с выборочными.

Так, для нормального распределения параметры m и берутся равными соответственно выборочным математическому ожиданию и дисперсии:

~	~
m mx ;	x .

Для показательного распределения параметр равен:

~1 . mx

Параметры равномерного распределения a и b будут равны:

	~	~			~	~
			3;				3.
	a mx	x			b mx	x

Параметр для распределения Рэлея равен:

	~		2
	mx			.

Приведѐм формулы для вычисления функции и плотности распределения. Для нормального распределения:

1

x m 2

x

x m

2 2

f x

x

e

; Fx x

f x

t dt Φ

0.5;

2

где (u) – интеграл Лапласа.

Для показательного распределения:

f x x

0;

x 0;

0;

x 0;

x 0;

Fx

x

e x ;

x 0.

e x ;

1

Для равномерного распределения:

0;

x a, b ;

0;

x a, b ;

f

x

x

1

F x

x a

)

;

x a, b ;

x

; x a, b ;

b a

b a

и для распределения Рэлея:

0;

x 0;

0;

x 0;

x2

2

f x x

x

Fx

x

x

2

e

2

;

x 0;

e

2

2

x 0.

2

1

На одном графике строятся теоретические и эмпирическая плотности выбранных распределений.

Эмпирическая плотность распределения представляет собой гистограмму, у которой масштаб по оси ординат изменѐн таким образом, чтобы площадь под кривой стала равна 1. Для этого все метки по оси ординат в гистограмме нужно разделить на nh, где n – число

109

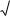
экспериментальных данных, а h – ширина интервала при построении гистограммы. Теоретические плотности распределения строим по приведенным выше соответствующим формулам.

Окончательный ответ по выбору теоретического распределения, которое лучше всего согласуется с экспериментальными данными можно получить с помощью критерия согласия.

Критерий согласия – это критерий проверки гипотезы о том, что случайная величина, представленная своей выборкой, имеет распределение предполагаемого типа.

Существует несколько критериев согласия. Чаще всего используются критерии Пирсона и Колмогорова.

В общем случае проверка состоит в следующем.

Рассчитывается критерий, как некоторая мера расхождения теоретического и эмпирического распределений, причем эта мера является случайной величиной.

Чем больше мера расхождения, тем хуже согласованность эмпирического распределения с теоретическим. Если она больше установленного критического значения, то гипотезу о выборе закона распределения следует отвергнуть, как мало правдоподобную. В противном случае экспериментальные данные не противоречат принятому распределению.

Критерий согласия Колмогорова

Критерий согласия Колмогорова применяется для проверки правильности подбора теоретического распределения. Для его применения нужно найти максимальную по модулю разность между теоретической (генеральной, предполагаемой, подобранной) функцией распределения Fx(x) и выборочной (опытной, эмпирической,

экспериментальной) ~ :

Fx x

		~	x
D max		Fx x Fx		,
x							-распределения
а по ней вычислить			D n , которую сравнить с квантилем

Колмогорова. Если величина не очень большая (не превосходит квантиля p), то на уровне значимости p статистическую гипотезу можно принять. Если же >p, то теоретическое распределение подобрано неверно.

График эмпирической функции распределения ~ представляет ступенчатую

Fx x

линию - ломаную со ступеньками высотой 1/n в точках с абсциссами xi.

Максимум разности между теоретической и эмпирической функциями распределения достигается как раз на одной из этих ступенек. Вычисляется в этих точках

~ и все подобранные F (x), и для каждой F (x) рассчитывается значение D. Из этих D

Fx x x x

выбирается минимальная, она и будет соответствовать наиболее подходящему виду распределения.

110