моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

Математическая модель представляет собой совокупность соотношений (уравнений, логических условий, операторов), определяющих характеристики процесса функционирования системы в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды, начальных условий и времени (в рамках степени приближения к действительности).

Агрегативная модель

В 1960-х годах было введено понятие класса моделей сложных систем, названных

агрегативными.

Основным элементом построения таких моделей был кусочно-линейный агрегат (КЛА). Эти модели обладают рядом привлекательных свойств, позволяющих использовать их в рамках общей схемы исследования сложных систем. В работах отечественной научной школы интенсивно исследовались их структурные и поведенческие свойства, создана имитационная система АИС (агрегативная имитационная система), базирующаяся на понятии агрегативной модели.

Рассмотрим определения и конструкции, приведенные ниже, в форме, приближенной к их программной реализации.

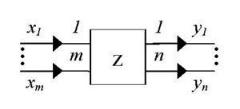
КЛА относится к классу объектов, которые принято изображать в виде преобразователя (рис. 2.1), функционирующего во времени и способного воспринимать входные сигналы х со значениями из некоторого множества X, выдавать выходные сигналы у со значениями из множества Y и находиться в каждый момент времени в некотором состоянии z из множества Z.

Рис.2.1. Общий вид преобразователя

Класс КЛА отличает специфика множеств X, Y, Z, допустимые формы входных и выходных сообщений (т. е. функций х (t) и у (t)), траекторий z(t), , а также способ преобразования входного сообщения в выходное. Отметим, что динамика КЛА носит ―событийный‖ характер.

В КЛА могут происходить события двух видов: внутренние и внешние.

Внутренние заключаются в достижении траекторией КЛА некоторого подмножества состояний; внешние – в поступлении входного сигнала.

Между событиями состояние КЛА изменяется детерминированным образом. Каждому состоянию z ставится в соответствие величина, трактуемая как потенциальное время до наступления очередного внутреннего события. Состояние КЛА в момент t* – наступление события является случайным.

В момент t*, наступления внутреннего события, выдается выходной сигнал у*, содержание которого зависит лишь от z*. В частности, выходной сигнал может быть и

31

пустым, т. е. не выдаваться. После случайного скачка x (z) вновь определяется время до наступления внутреннего события.

Рассмотрим момент t** наступления внешнего события, связанного с поступлением входного сигнала. Тогда состояние КЛА в момент t** является случайным, зависящим лишь от х и z**. В момент t**, выдается выходной сигнал у **, содержание которого определяется х и z**.

Условимся считать, что если моменты наступления внешнего и внутреннего событий совпадают, то изменение состояния осуществляется в соответствии с правилом наступления внешнего события, т. е. входные сигналы имеют приоритет над внутренними событиями.

Таким образом, динамику КЛА можно представить в следующем виде.

Пусть в некоторый момент задано состояние КЛА. Тогда определяется время T(z), через которое совершается случайный скачок, и меняется состояние. Начиная с момента наступления события (внешнего или внутреннего), ситуация повторяется, и динамику КЛА можно описать в виде задания фазовой траектории изменения состояний z (t).

Процесс функционирования КЛА полностью определяется изменениями, происходящими в особые моменты времени – моменты наступления событий (внешних или внутренних). Между особыми моментами состояние КЛА меняется детерминировано.

Опишем теперь КЛА более подробно. КЛА внешне имеет вид многополюсника с m входными клеммами и n выходными клеммами (рис.2.2). Отметим, что в общем случае для различных КЛА.

Рис.2.2. Кусочно-линейный агрегат

Предположим, что в состав множеств Xi и Yj включены и фиктивные элементы 0, наличие которых на входе или выходе КЛА означает отсутствие сигнала на соответствующей входной или выходной клемме.

Рассмотрим, на чем основана программная реализация агрегативных моделей.

Не фиктивными входными хi или выходными yj сигналами, а также состояниями z КЛА являются данные.

Данными считаются: элементарные данные; списки данных; массивы данных; структуры данных. Элементарными данными считаются целые числа, действительные числа, символьные переменные. Здесь термины ―список‖, ―массив‖ употребляются в их обычном смысле. Понятие структуры данных соответствует дереву, на корнях которого размещены данные. Каждое данное имеет свое имя. Рассматриваемые данные хорошо отображают содержательные представления, существующие у исследователя

32

относительно реальных объектов, и существенно облегчают процесс построения модели. Эти данные удобны как с математической, так и с программной точек зрения.

Пусть состояние z КЛА определено как некоторая структура данных. Тем самым фиксирован вид дерева, представляющего эту структуру.

Дерево базируется, в конечном счете, на элементарных данных. Обозначим через Iz элементарные данные, входящие в состояние z и имеющие тип целых чисел и символов, а через Rz , – элементарные данные, имеющие действительный тип. Предположим, что значения и состав элементарных данных могут меняться лишь в особые моменты времени, а между ними остаются постоянными. Разобьем множество Rz на два подмножества R =, где состоит из положительных величин, a – из неположительных. Будем считать, что данные из подмножества остаются неизменными между особыми моментами времени. Это отвечает обычно используемой ―энергетической интерпретации‖ причин наступления внутренних событий в моменты, когда исчерпывается некоторый ресурс, заканчивается операция и т. д. Таким образом, внутреннее событие происходит, когда хотя бы один из положительных элементов множества обращается в нуль.

Выводы

Таким образом, математическое моделирование — это теоретико-

экспериментальный метод познавательно-созидательной деятельности, исследования и объяснения явлений, процессов и систем (объектов-оригиналов) на основе создания новых объектов - математических моделей.

Сущность моделирования заключается в том, что взаимосвязь исследуемых явлений и факторов передается в форме конкретных математических уравнений.

Процесс построения математической модели включает в себя следующие типовые этапы:

-определение целей моделирования;

-качественный анализ системы, исходя из этих целей;

-формулировка законов и правдоподобных гипотез относительно структуры системы, механизмов ее поведения в целом или отдельных частей;

-идентификация модели (определение ее параметров);

-верификация модели (проверка ее работоспособности и оценка степени адекватности реальной системе);

-исследование модели (анализ устойчивости ее решений, чувствительности к изменениям параметров и пр.) и эксперимент с ней.

Под математической моделью принято понимать совокупность соотношений (уравнений, неравенств, логических условий, операторов и т.п.), определяющих характеристики состояний объекта моделирования, а через них и выходные значения – реакции, в зависимости от параметров объекта-оригинала, входных воздействий, начальных и граничных условий, а также времени.

33

Математическая модель, как правило, учитывает лишь те свойства (атрибуты) объекта-оригинала, которые отражают, определяют и представляют интерес с точки зрения целей и задач конкретного исследования. Следовательно, в зависимости от целей моделирования, при рассмотрении одного и того же объекта-оригинала с различных точек зрения и в различных аспектах, он может иметь различные математические описания и, как следствие, быть представлен различными математическими моделями.

Принимая во внимание изложенное выше, дадим наиболее общее, но в то же время строгое конструктивное определение математической модели, сформулированное П.Дж.Коэном.

Математическая модель — это формальная система, представляющая собой конечное собрание символов и совершенно строгих правил оперирования этими символами в совокупности с интерпретацией свойств определенного объекта некоторыми отношениями, символами или константами.

34

Лекция 3. Типовые математические модели

На лекции рассматриваются основы теории марковских процессов и типовые аналитические модели, основанные на допущении о марковости протекающих в моделируемых объектах процессов.

Примеры моделей

Оптимизационные модели

Математическая оптимизационная модель должна содержать следующие основные компоненты:

1.Переменные – значения, которых необходимо вычислить.

2.Целевая функция – цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти ее максимум или минимум.

3.Ограничения – записанные, математически ограничения, выявленные из анализа предметной ситуации.

Рассмотрим несколько примеров постановки задачи оптимизационных моделей.

Задача распределения ресурсов

На предприятии, выпускающем неоднородную продукцию, руководители хотят определить уровни производства этой продукции на некоторый период времени.

Исходные данные:

-количество материалов (X, Y, Z), требуемых на каждом этапе технологического процесса для выпуска единицы продукции;

-объем запасов этих материалов на складе;

-доход, получаемый в результате выпуска единицы продукции.

Цель планирования – увеличение прибыли.

Результаты анализа проблемной ситуации были сведены в табл. 3.1. Таблица 3.1

						Этапы технологического процесса					В наличии
					1		2	3		4	ресурсов
		литры, ящики		количество	1		1	1,5		2	30
Требуемые ресурсы	(кг, бочки,			материала X
			т.п.).	количество	2		5	3		7	120
				материала Y
				количество	3		5	10		15	100
				материала Z
				Доход с
				единицы	4		5	9		11
				продукции
				Объем выпуска	x1		x2	x3		x4
				продукции

35

Суммарная прибыль составит 4x1+5x2+9x3+11x4. Это и есть целевая функция, которую необходимо максимизировать.

Ограничения: суммарные затраты на производство продукции из каждого материала не должны превышать имеющегося объема этого материала в наличии.

Таким образом, модель записывается в виде целевой функции (критерия):

4x1+5x2+9x3+11x4 → max.

и ограничений:

x1 + x2 + 1,5x3 + 2x4 30, 2x1 + 5x2 + 3x3 + 7x4 120, 3x1 + 5x2 + 10x3 +15x4 100, x1 0, x2 0, x3 0, x4 0.

Транспортная задача

Требуется составить план перевозок, минимизирующий затраты на перевозки. Исходные данные:

А1….., Аn - пункты отправления; а1……,аn - объѐмы продукции; В1……,Вm - пункты назначения; b1……,bm - потребности в продукции;

lij – стоимость перевозки единицы продукции из Ai в Bj; j = 1,…, m,

i = 1,…, n.

xij – объѐм продукции, перевозимой из Ai в Bj.

Целевая функция (общая стоимость перевозки) имеет следующий вид:

lij xij

i			j	→ min,
ограничения:
xij				b j ;
	i
				ai ;
xij
	j
x		ij	0.

Рассмотренные оптимизационные модели являются линейными и решаются методами линейного программирования.

Особенности дескриптивных моделей

Отличительной особенностью дескриптивных (описательных) моделей является отсутствие целевой функции.

36

Основной задачей подобных моделей является описание процесса с помощью математического аппарата в целях изучения поведения систем и прогнозирования их дальнейшего развития.

Кописательным моделям относятся следующие виды моделей:

Регрессионные модели – описывают функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме.

Модели кластеризации – описывают группы (кластеры), на которые можно разделить объекты, данные о которых подвергаются анализу. Группируются объекты (наблюдения, события) на основе данных (свойств), описывающих сущность объектов. Объекты внутри кластера должны быть "похожими" друг на друга и отличаться от объектов, вошедших в другие кластеры. Чем больше похожи объекты внутри кластера и чем больше отличий между кластерами, тем точнее кластеризация.

Модели ассоциации – выявление закономерностей между связанными событиями. Примером такой закономерности служит правило, указывающее, что из события X следует событие Y. Такие правила называются ассоциативными.

Описательные модели находят свое применение во многих областях, например:в практике маркетинговых исследований

например, "модель потребления", характеризующая бюджет потребителя и др.; моделирование движения объектов производится с целью предсказания траектории полета. В этом случае цели моделирования носят описательный характер, поскольку нет никаких возможностей повлиять на суть происходящих процессов.

интеллектуальный анализ данных при этом описательные модели нацелены на анализ структуры данных, определение

правил, шаблонов и ассоциаций внутри данных. К таким моделям относятся, например, кластеризация, классификация, таблицы взвешенных оценок, анализ ассоциаций.

описательные модели отражают содержание и основные свойства экономических объектов как таковых

Сих помощью вычисляются числовые значения экономических факторов и показателей. К таким моделям можно отнести экономико-статистические или эконометрические модели.

Как правило, эти модели дают общие представления об объекте, процессы в моделируемом объекте отображаются в агрегированном виде, максимально обобщены. Но, несмотря на это, значимость этих моделей велика, так как они позволяют изучать явления целиком, комплексно и позволяют обнаружить фундаментальные свойства объектов и процессов. Методами исследования и построения этих моделей являются методы и критерии математической статистики

37

F g V 0 ,

(корреляционный, регрессионный анализ и пр.). Информационной базой, как правило, являются статистические выборки и временные ряды.

Область применения этих моделей: достаточно широка: модели экономики страны, модели расширенного воспроизводства, модели спроса и предложения, производственные функции.

Основные подходы к моделированию

Обзор перечисленных моделей говорит о большом их многообразии и проникновении математики в трудноформализуемые области. В связи с этим возникает вопрос о существовании общих подходов к моделированию. Рассмотрим основные из них.

Использование законов природы

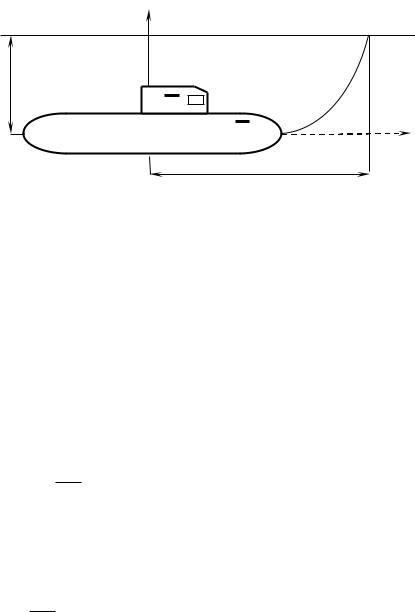
Пример 1. Всплытие подводной лодки (используются законы Архимеда и Ньютона).

h

H

l

Рис. 3.1 Всплытие подводной лодки

Предположим, что в момент времени t = 0, когда лодка находится на глубине H и движется по горизонтали с постоянной скоростью , получен приказ о подъеме (рис. 3.1). Временем вытеснения воды из цистерн и заполнением их воздухом пренебрегаем, таким образом, в момент времени t = 0 начинает действовать выталкивающая сила.

Требуется определить вид траектории всплытия лодки. По закону Архимеда:

где g = 9,81 м/с2; V – объѐм лодки;

0 – плотность воды.

В соответствии со вторым законом Ньютона можно записать:

1V d 2 h F P gV ( 0 1 ) , dt 2

где 1 – плотность лодки;

1V – масса лодки;

F– сила Архимеда;

d 2 h – ускорение; dt 2

38

Vmax

7 км с

P– вес лодки.

Решением уравнения второго закона Ньютона является:

	h(t)		1		g		0 1		t 2 .
			2				1
	С учетом l(t) v t									и t	l(t)	получим уравнение искомой траектории:
											v
	h(l)		1	g			0 1		l 2 .
			2					v2
							1

Таким образом, траектория всплытия лодки представляет собой параболу с вершиной в точке l 0, h 0 .

Пример 2. Полет ракеты (используется закон сохранения количества движения (импульса)).

Рассмотрим некоторый момент времени t и интервал dt, согласно закону сохранения количества движения можно записать:

m dV U dm ,

где V – скорость ракеты; m – масса ракеты;

U – скорость выброса сгораемого топлива.

Делением обеих частей на dt последнее уравнение преобразуется к дифференциальному уравнению:

m dVdt U dmdt .

Решение уравнения является функция:

	V (t) U n	m0	,
		m(t)

где m0 – начальная масса; m(t) – масса в момент . Максимальная скорость:

	Vmax	U n		m0	,
			mП	mK

где mП – масса полезная; mK – масса конструкции.

Для одноступенчатой ракеты mK 0.1m0 . Получается, что даже без полезного груза (mП = 0) при реальной скорости истечения газов ( U 3км с ) максимальная скорость будет равна: , т.е., скорость ракеты меньше, чем первая космическая скорость, что говорит о невозможности выхода на орбиту.

Таким образом, для решения этой задачи необходимо использовать многоступенчатые ракеты.

39

Принцип аналогии

Оказывается электрическая, механическая, гидравлическая, пневматическая и тепловая системы имеют много общего.

Они переносят и преобразовывают некоторую физическую субстанцию: электрические – заряд, механические – массу, гидравлические - жидкость, пневматические – газ.

Применение аналогий основано на одном из важнейших свойств моделей – их универсальности, т.е. применимости к объектам принципиально различной природы.

Для решения задач моделирования, основываясь на принципе аналогии подобные системы можно представить как совокупность простых элементов типа резистора, оказывающего сопротивление переносу субстанции, конденсатора, обладающего свойством инерционности, что проявляется в стремлении сохранить поток субстанции неизменным.

Использование типовых моделей

Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем.

Однако в практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы:

дифференциальные и интегральные уравнения,

конечные и вероятностные автоматы,

системы массового обслуживания,

сетевые модели,

игровые модели.

Внастоящее время активно развивается новый подход, использующий модели процессов поведения сложных систем, основанные на многоагентных технологиях. Предполагается, что формализуемые процессы представляются в виде взаимодействия различных команд программных агентов в динамической среде.

Не обладая такой степенью общности, как рассмотренные модели, типовые математические схемы имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения.

Вкачестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегро-дифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени,— конечные автоматы и конечно-разностные схемы.

Вкачестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а

40