моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

для представления системы с непрерывным временем — системы массового обслуживания и т. д.

Перечисленные типовые математические схемы, естественно, не могут претендовать на возможность описания на их базе всех процессов, происходящих в больших информационно-управляющих системах.

Для таких систем в ряде случаев более перспективным является применение агрегативных моделей.

Агрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей.

Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывнодетерминированный (например, дифференциальные уравнения); дискретнодетерминированный (конечные автоматы); дискретно-стохастический (вероятностные автоматы); непрерывно-стохастический (системы массового обслуживания); обобщенный, или универсальный (агрегативные системы).

Иерархический подход к получению моделей

Редко бывает, что модель строится с учетом сразу всех факторов, существенных для поведения системы. Поэтому естествен подход, реализующий принцип «от простого к сложному», когда следующий шаг делается после достаточно подробного изучения не очень сложной модели. При этом возникает цепочка (иерархия) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качестве случая.

Процесс построения моделей

Этапы процесса построения моделей можно представить в следующей последовательности:

1.Построение модели начинается со словесного описания объекта или явления, т.е. сформировывается предметная модель. Формулируется цели исследования модели

2.Выбирается или формулируется закон, которому подчиняется объект. Модель записывается в математической форме.

3.Завершается построение модели. Проводится селекция факторов, при которой отбрасываются несущественные и малозначимые факторы.

4.Построенная модель исследуется с применением различных подходов и делается вывод о ее адекватности, т.е. соответствии объекту и целям исследования.

41

Конечные автоматы

Понятие конечного автомата

Теория автоматов является разделом теоретической кибернетики, в которой изучаются математические модели – автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции и целесообразной степени общности.

Автомат можно рассматривать как некоторое устройство (черный ящик), на которое подаются входные сигналы, снимаются выходные и которое может иметь некоторые внутренние состояния.

Состояние – это то, на что влияет управление, и что вместе с управлением определяет результат (выход).

Разностное уравнение для состояния такой системы имеет вид:

x(t t) (x(t),u(t))

(1.4.1)

В уравнении (1.4.1) вычтем слева и справа одну и ту же величину x(t), тогда

x(t t) x(t) (x(t)u(t)) x(t).

(1.4.2)

Разделим левую часть уравнения (1.4.2) на t, t устремим к нулю и в итоге получим запись дифференциального уравнения в пространстве состояний:

x(t) 2 (x(t), u(t)).

Конечным автоматом называется автомат, у которого множество внутренних состояний, входных и выходных сигналов являются конечными множествами.

Таким образом, по сравнению с универсальной моделью существует ограничение: конечность множеств. Данное ограничение не существенно, что позволяет широко применять конечные автоматы, в основном для синтеза устройств управления. Конечные множества (управлений, состояний, выходных сигналов) называются также алфавитами.

Конечный автомат является в общем случае динамической системой, для которой характерны переходные процессы, но сигналы не непрерывны, а дискретны. Разделение текущего времени связывают с изменениями внутреннего состояния и входа. Поэтому интервалы дискретности могут быть неодинаковыми. Внутренние состояния могут иметь различную степень детализации. Поэтому можно говорить о более быстрой и более медленной тактности.

Как и у любой динамической системы, работа конечного автомата описывается двумя функциями:

x(t 1) (x(t),u(t)) - функция переходов, y(t) f (x(t),u(t)) - функция выхода,

где x – переменная состояния;

u – переменная управления;

42

y – переменная выхода;

t – момент времени (t = 0,1,2,3…).

Все эти переменные в общем случае являются векторами.

С помощью этих двух функций можно, зная начальное состояние и последовательность управлений, определить состояния и выходы во все последующие моменты времени.

Время задается некоторым тактовым источником, но такты не обязательно должны быть постоянной длительности. Ввиду дискретности всех переменных они меняются скачкообразно, и нет необходимости дробить время между моментами соседних изменений управления или состояния более мелко. Поэтому можно считать, что моменты времени определяются сменой управления или состояний.

Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии x(t), подается некоторый сигнал u(t), на который автомат реагирует переходом в (t+1)-м такте в новое состояние x(t+1) и выдачей некоторого выходного сигнала.

По числу состояний различают конечные автоматы с памятью и без памяти.

Автоматы с памятью имеют более одного состояния, а автоматы без памяти обладают лишь одним состоянием.

По характеру отчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных автоматах моменты времени, в которые автомат считывает входные сигналы, определяются принудительно сихронизирующими сигналами. После очередного сигнала, с учетом считанного, происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхроимпульсами. Асинхронный автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины, он может несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое состояние, которое уже не может быть изменено данным входным сигналом.

Задание автомата в виде таблицы и графа

Автомат может быть задан своими функциями (переходов и выхода), таблично, в виде графа, матрицы, а также аналитически.

Для табличного представления нужно перечислить все сочетания x(t), u(t) – все элементы области определения функций переходов и выхода (область определения одна и та же) и записать соответствующие им значения x(t+1) и y(t) – элементы областей значения функций переходов и выхода.

Для наглядности аргументы x и u имеет смысл разделить: значения одного аргумента приписать строкам, а другого – столбцам. Тогда значение функций будут

43

записываться на пересечении строк и столбцов. Ввиду совпадения областей определения функций переходов и выхода эти функции можно задавать одной таблицей.

При изображении функций в виде графа: состояния приписывают вершинам, управления – дугам.

Пример 1. Пусть множество управлений u состоит из управлений α, β, γ, множество состояний x – состояний 1,2,3,4, т.е. u α, β, , x1,2,3,4 , y 0,1 .

Функции φ (переходов) и (выхода) заданы таблицей переходов (табл. 1.4.1), в которой единица может означать необходимость какого-либо действия, ноль – отсутствие такового, прочерк – ограниченность управлений (отсутствует управление β при состоянии 2 и управление γ при состоянии 3).

Таблица 1.4.1

	x(t)		u(t)
		α	β
	1	2/0	3/1	4/0
	2	2/1	-	3/0
	3	3/0	4/0	-
	4	2/1	1/0	2/1

При другом способе задания конечного автомата используется понятие направленного графа.

Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал вызывает переход из одного состояния в другой, то на графе автомата дуга, соединяющие их вершины обозначается соответствующим символом входного сигнала. Для задания функции выходов дуги графа необходимо отметить соответствующими сигналами.

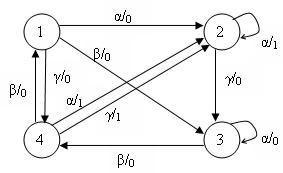
Табл. 1.4.1.соответствует граф, показанный на рис. 1.4.1.

Рис.1.4.1 Граф конечного автомата таблицы 1.4.1.

Пример 2. Рассмотрим автомат, который выдает билет при опускании в него монет в сумме 3 руб., причем он принимает монеты 50 коп., 1рубль и 2 рубля. Автомат может давать сдачу. Составим функцию перехода и выхода.

44

u α=0.5, β=1, =2 , x1,2,3,4,5,6 .

Функция переходов может быть задана таблицей переходов (табл. 1.4.2). Таблица 1.4.2

			u
		0.5	1.0	2.0
	x		β
0	1	2	3	5
0.5	2	3	4	6
1.0	3	4	5	1
1.5	4	5	6	1
2.0	5	6	1	1
2.5	6	1	1	1

Поясним табл. 1.4.2.

Например, опустили в автомат 1 рубль. Тогда из исходного состояния 1 (ожидание начала набора суммы) автомат перешел в состояние 3 (в автомате пока накопилась сумма 1 рубль). Теперь опустили, к примеру, 50 коп., тогда автомат перейдет из теперь уже исходного состояния 3 в состояние 4 (в автомате уже полтора рубля), далее опустили еще 1 рубль – автомат перешел из состояния 4 в состояние 6 (накопилась сумма 2,5 рубля). И, наконец, опустили последние 50 коп., в автомате собралась полная сумма: выдается билет, и автомат опять переходит в 1 состояние – готовности к приему монет.

Для функции выхода y = (y1, y2) составим табл. 1.4.3, в которой: y1 – сигнал на пропуск или выдачу билета, y1 0,1 .

y2 – сигнал для сдачи, y2 0, 0.5, 1.0, 1.5 .

Таблица 1.4.3

			u
		0,5	1	2
x			β
1		0;0	0;0	0;0
2		0;0	0;0	0;0
3		0;0	0;0	1;0
4		0;0	0;0	1;0,5
5		0;0	1;0	1;1
6		1;0	1;0,5	1;1,5
действие			сдача

При превышении требуемой цены за билет вместе с билетом выдается сдача. Моменты времени лучше связывать только с моментами опускания монеты.

45

Матричное задание автомата

Граф переходов, как и любой граф, может быть представлен матрицей переходов – квадратной матрицей, размерность которой совпадает с числом состояний, а элементами являются дуги, соединяющие состояния.

Запишем автомат в виде матрицы:

		0			0		0
		0	0			0
			0	0			0
	А
			0	0	0
			0	0	0	0
			0	0	0	0	0

Если множество путей, ведущих от одного состояний к другому записывать как сумму, а путь, включающий дуги как произведение дуг, то возведение матрицы в степень дает все пути определенной длины, совпадающей с показателем степени между состояниями (возведем в квадрат, получим пути между состояниями длины 2, если в куб - длины 3).

Если хотят определить количество путей определѐнной длины, то составляют так называемые скелеты матриц и возводят их в степень. Они отличаются от матрицы «А» тем, что в ней вместо управлений записывается их количество.

				0		1	1	0	1	0								3 0			1	2	1	2
					0	0	1	1	0	1									5	0	0	1	2	1
~					1	0	0	1	1	0			~ 2						3	1	1	0	2	2
A												;	A
				1		0	0	0	1	1								5 1			1	0	1	1
					2	0	0	0	0	1									3	2 2		0	2	0
					3	0	0	0	0	0									0	3 3		0	3	0

Транспортная сеть, рассмотренная ранее в примере минимизации, расстояния также подходит под модель конечного автомата.

Путем возведения матрицы переходов в степень можно получить пути определенной длины, ведущие от i-го состояния к j-му для всех i и j.

Обозначим множество дуг, ведущих из i-го состояния в j-ое в графе переходов, через πij (получится одна объединенная дуга).

Путь – это последовательность дуг. Будем считать его произведением дуг.

Путь между состояниями может быть не один. Если множество путей записывать как сумму, то возведение матрицы переходов в квадрат дает все пути длины 2 между всеми состояниями. Справедливость этого подтверждается правилом перемножения матриц.

46

Элемент, стоящий на пересечении i-ой строки и j-го столбца произведения матриц равен произведению i-ой строки и j-ый столбец матриц-сомножителей. При возведении в квадрат это есть произведение следующих строки и столбца

						1 j
	A					2 j
				i1	i 2	ij	is
						sj

То есть ij = i1 1j + i2 2j + …+ is sj .

Это есть все пути длины 2, ведущие из i-го состояния в j-е.

Аналогично элемент (i,j) матрицы ||A||k является множеством всех путей длины k, ведущих из i-го состояния в j-е состояние автомата A.

Матрица ||A||k называется матрицей переходов k-го порядка.

Если необходимо определить пути, ведущие из одного состояния, например i-го, то нужно на матрицу ||A|| умножить не матрицу, а ее i-ю строку. После каждого умножения

получается строка. В результате будет строка, содержащая пути определенной длины из i-го состояния.

Таким образом, понятие автомата в дискретно-детерменированном подходе к исследованию на моделях свойств объектов является математической абстракцией, удобной и эффективной для описания широкого класса процессов функционирования реальных объектов в автоматизированных системах (элементы ЭВМ, устройства контроля, регулирования и управления, системы коммутации). Для подобных систем характерно наличие дискретных состояний и дискретный характер работы во времени. Но широта их применения не означает универсальности этих математических схем. Например, данный подход непригоден для описания процессов принятия решений, процессов в динамических системах с наличием переходных процессов и стохастических элементов.

Минимизация конечных автоматов

Понятие эквивалентности

С практической точки зрения при функционировании автомата представляет интерес, в основном, зависимость между входами и выходами автомата. В этом случае роль автомата сводится к формированию этих зависимостей и любая совокупность состояний, обеспечивающая требуемые зависимости между входом и выходом, может быть выбрана в качестве множества состояний автомата.

Эта возможность привела к одной из важных задач теории конечных автоматов – минимизации автоматов, заключающаяся в сокращении числа состояний путем объединения эквивалентных состояний.

Состояния называются эквивалентными, если поведение автомата одинаково независимо от того, какое из них является исходным.

47

Другими словами, выходная последовательность, вырабатываемая автоматом при подаче на вход произвольной входной последовательности, и при начальном состоянии из эквивалентных, зависит только от входной последовательности и не зависит от того, какое из эквивалентных состояний является исходным.

Эквивалентные автоматы неразличимы по реакции на выходе, но могут иметь различное количество внутренних состояний, и, следовательно, могут отличаться внутренними состояниями при одинаковых входных данных.

Для определения эквивалентных состояний используется понятие «k – эквивалентности».

Состояние называется k-эквивалентным, если автомат, находясь в любом из них,

имеет одинаковое поведение в течение k тактов. k-эквивалентные состояния образуют k- эквивалентные классы.

Очевидно, что при малых k число k-эквивалентных состояний больше, чем при больших k (а число k-эквивалентных классов меньше). Это позволяет указать путь определения эквивалентных состояний. Он заключается в разбиении состояний автомата на k-эквивалентные классы поочередно для k = 1,2,3…. Число таких классов постепенно растет, размер классов уменьшается, и в итоге в них останутся только эквивалентные состояния. Классы, которые невозможно разбить являются классами эквивалентных состояний.

Пример определения эквивалентных состояний автомата

Автомат с тремя исходными состояниями

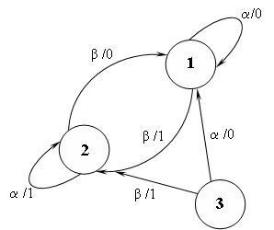
Автомат представлен в виде графа (рис.1.5.1). Определим, есть ли у автомата эквивалентные состояния.

Рис. 1.5.1 Представление автомата в виде графа

Графу соответствует таблица переходов (табл. 1.5.1).

48

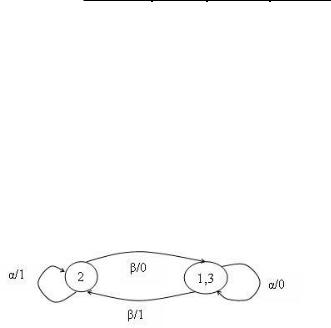
Таблица 1.5.1

	x	U
			β
	1	1/0	2/1
	2	2/1	1/0
	3	1/0	2/1

Произведем первое разбиение автомата, которое приведено в табл. 1.5.2. Таблица 1.5.2

			U
Классы	x			β
I	1	1		2
	3
		1		2
II	2	2		1

Состояния 1 и 3 объединены в один класс, поскольку на любое входное воздействие автомат при этих состояниях реагирует одинаково (состояния не различаются по выходам).

Из табл. 1.5.2 видно, что дальнейшее разбиение невозможно, поскольку при любом входе состояния 1 и 3 одного класса, который только и можно разбить, переходят в состояние одного класса (либо 1, либо 2), которые неразличимы.

Таким образом, автомат можно упростить и представить в виде графа (рис. 1.5.2) и таблицы переходов (табл. 1.5.3.).

Рис. 1.5.2 Граф минимизированного автомата

Таблица 1.5.3

x		u
	α		β
1,3	1/0		2/1
2	2/1		1/0

Автомат с пятью исходными состояниями

Пример 2. Автомат задан в виде табл. 1.5.4.

49

Таблица 1.5.4

	x		u
			β	γ
	1	2/0	5/1	3/0
	2	3/1	1/0	4/1
	3	5/0	4/1	1/0
	4	2/0	3/1	1/0
	5	4/1	1/0	3/1

В этом автомате два 1-эквивалентных класса.

Проведем разбиение состояний на эти классы (табл. 1.5.5.). Таблица 1.5.5

	Классы	x		u
				β	γ
		1	2	5	3
		3	5	4	1
		4	2	3	1
		2	3	1I	4
		5	4	1I	3

При подаче β из состояние 1 автомат переходит в класс II, а из 3 и 4 в класс I, которые различимы при любом входном воздействии. В итоге получим таблицу разбиения (табл. 1.5.6).

Таблица 1.5.6

	Классы			U
		x		β	γ
		1	2III	5III	3II
		3	5	4	1I
		4	2	3	1
		2	3	1I	4
		5	4	1I	3

Дальнейшее разбиение невозможно. Таким образом, получена результирующая таблица состояний (табл. 1.5.7).

50