моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

Таблица 1.5.7

		U
Классы
		β	γ
	/0	/1	/0
	/0	/1	/0
	/1	/0	/1

Рассмотренные автоматы называются синхронными. В синхронных автоматах все состояния являются устойчивыми, так как в них автомат может находиться неограниченно долго, поскольку переход в следующее состояние возможен после подачи очередного тактового сигнала.

Существуют и асинхронные автоматы, в которых нет синхронизации или тактирующих сигналов. Асинхронный автомат задерживается неограниченно долго только в устойчивых состояниях. Устойчивое состояние характеризуется тем, что в следующий момент времени при продолжающем действовать управлении автомат вновь стремится к этому состоянию, т.е. если состояние x* устойчивое при управлении u*, то

(x* (t),u(t)) x* (t) .

Может оказаться, что при некотором управлении автомат постоянно будет неустойчивым, превращаясь в генератор. Ввиду ограничений в смене управлений асинхронный автомат менее управляем, чем синхронный.

Аналитическое задание конечных автоматов

Основные правила преобразования формул алгебры логики

Можно выделить следующие достоинства аналитического представления конечных автоматов:

компактность записи по сравнению с табличным, графовым или матричным заданиями;

простота моделирования работы конечных автоматов на ЭВМ;

аналитическое представление необходимо при синтезе структуры автомата, так как при таком задании функции функциональных преобразователей выражаются через элементарные функции, реализуемыми простыми элементами.

Для формального описания цифровых управляющих устройств широко применяется аппарат алгебры логики.

Логической (булевой) переменной называется величина, которая может принимать только два значения.

Логической функцией (булевой функцией) называется функция логических переменных, принимающая только два значения 0 и 1.

51

Различные комбинации значения входных переменных функций называются наборами.

Функция является полностью заданной, если указаны ее значения для всех наборов. Сопоставляя каждому набору значение функции можно задать функцию с помощью таблицы, называемой таблицей истинности или таблицей соответствия.

Для аналитической записи функций алгебры логики можно использовать различные множества элементарных функций, требуется только, чтобы они составляли функционально полную систему, т.е. систему, с помощью которой можно записать любую функцию. Как правило, используют ОФПС (основная функционально полная система), включающую операции &, и инверсию (табл. 1.6.1).

Для более глубокого изучения вопросов аналитического представления систем можно обратиться к Хаггарти Р. Дискретная математика для программистов. М.: Техностфера, 2012 – 400 с.

Таблица 1.6.1

x	y	x & y	x y	x	y
0	0	0	0	1	1
0	1	0	1	1	0
1	0	0	1	0	1
1	1	1	1	0	0

Правила преобразования формул, предназначенных для упрощения выражений и перехода от табличного задания функции к аналитическому следующие:

Правила преобразования

1.x y y x

правило коммутативности

xy y x

2. x y z x y z		правило ассоциативности (сочетательный закон)
x y z x y z

3. x y z xy xz		правило дистрибутивности (распределительный закон)
x yz x y x z

4. x x

- правило де Моргана.
x y x y
x y x y
f x1 , x2 ,....xn , , f x1 ,	x2 , .....,xn , ,

f a,b, c, d a bc b c abd

f a,b, c, d a b c b c a b d

52

(xy yz)(x v ) (xy yz)x (xy yz)v

(xyz) (xz) ( yz)

5. 1 x 1

0 x x

x x x x x 1

x f		f x		f	f	склеивание
	x		x
x x f x 1 f x						поглощение

1 x x

x f

f

0 x 0

f

склеивание

x

x x 1

x x f x

поглощение

x x 0

6. x1 f x1 , x2 ,....,xn x1

f 1, x2 ,....,xn

1 f x1 , x2

,.....,xn

1 f 0, x2 ,....,xn

x

x

x1 f x1 x2

,....,xn x1

f 0, x2 ,....,xn

f x1 x2

,.....,xn

1 f 1, x2 .....,xn

x1

x

Разложение функций на конституенты и переход от табличного задания функции к аналитическому

Рассмотрим, как можно перейти от табличного задания алгебры логики к аналитическому заданию. Для этого сначала определим понятия нормальных форм.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного числа различных членов, каждый из которых представляет собой конъюнкцию отдельных переменных или их отрицаний, входящих в данный набор не более одного раза, например, .

Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа различных членов, каждый из которых представляет собой дизъюнкцию отдельных переменных или их отрицаний, входящих в данный набор не более одного раза, например, (x y z)(x z)( y z) .

Приведение булевых соотношений к нормальной форме проводится следующим образом:

-с помощью законов де Моргана формулы преобразуются к такому виду, чтобы знаки отрицания относились только к отдельным переменным:

-на основе законов дистрибутивности формула сводится к дизъюнкции конъюнкций или конъюнкции дизъюнкций;

-полученное выражение далее упрощается.

____

Пример 1. Преобразовать выражение (xy yz) xv к ДНФ.

Решение. С помощью законов де Моргана преобразуем конъюнкцию последних двух членов:

____

(xy yz) xv (xy yz)(x v ) .

После раскрытия вторых скобок получим:

.

53

После раскрытия всех скобок выражение приводится к окончательному виду:

(xy yz)x (xy yz)v xy yxz vxy vyz .

Полученное выражение является ДНФ.

Если в каждом члене нормальной формы представлены все переменные либо в прямом, либо в инверсном виде, то такая нормальная форма называется совершенной нормальной формой:

xyz xyz xyz - СДНФ,

(x y)(x y) - СКНФ.

Если какой-нибудь член дизъюнктивной или конъюнктивной нормальной формы не содержит какой-либо переменной, то она вводится тождественным преобразованием.

Пример 2. Привести к СДНФ: xy xyz .

Решение. Введем недостающий член и получим ответ: xy(z z) xyz xyz xyz xyz .

Пример 3. Привести к СКНФ: (x y)x .

Решение. Также как и в предыдущем примере введем н6едостающий член:

(x y)x yy (x y)(x yy) .

С учетом (x yy) (x y)(x y) после преобразований получим искомый вид СКНФ:

(x y)(x y)(x y) (x y)(x y) .

Конституентой единицы ( К е ) называют конъюнкцию, содержащую все переменные или их инверсии, которая обращается в единицу только при одном выборочном наборе переменных.

Например, конституенте единицы К е x1x2 x3 x4 соответствует набор 0100. При этом наборе в К е входят только единицы, что обеспечивает равенство К е =1, при других значениях переменных К е = 0.

Конституентой нуля ( К н ) называют дизъюнкцию, содержащую все переменные или их инверсии, которая обращается в нуль только при одном выборочном наборе

переменных.
Например,	конституенте нуля К н x x	2	x	x	4	соответствует набор 1011. При
	1		3
этом наборе в	К н входят только нули, что обеспечивает равенство К н = 0, при других
значениях переменных К н = 1.

Так как булева функция, представленная в виде СДНФ является дизъюнкцией конституент единицы, то она обращается в единицу только при наборах значений переменных, соответствующих конституентам единицы, а на остальных наборах значений эта функция обращается в нуль.

Аналогично, так как булева функция, представленная в виде СКНФ является конъюнкцией конституент нуля, то она обращается в нуль только при наборах значений

54

fСКНФ

fСДНФ

переменных, соответствующих конституентам нуля, а на остальных наборах значений эта функция принимает значение единицы.

Обратное утверждение также справедливо, что дает возможность сформулировать правила перехода от табличного представления функции к аналитическому:

-для представления булевой функции в СДНФ необходимо записать дизъюнкции конституент единицы, соответствующих наборам значений переменных, на которых функция принимает значение, равное единице,

-для представления булевой функции в СКНФ необходимо записать конъюнкции конституент нуля, соответствующих наборам значений переменных, на которых функция принимает значение, равное нулю.

Пример 4. Имеем табличное представление функции (табл. 1.6.2). Таблица 1.6.2

a	b	c	f
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

Для СДНФ запишем конституенты единицы:

K1e ab c , K 2e abc , K3e abc , K 4e ab c , K5e abc .

Тогда функция в виде СДНФ будет равна:

a b c a b c a bc abc abc .

Для СКНФ запишем конституенты нуля:

K1н a b c , K2н a b c , K3н a b c .

Функция в виде СКНФ будет иметь вид:

a b c a b c a b c .

Для практической реализации надо брать ту совершенную форму, которая содержит меньше конституент, так как это позволяет реализовать логическое устройство с меньшим количеством элементов.

Недостатки способа перехода от табличного задания к аналитическому через конституенты:

55

-громоздкость (требуются дальнейшие преобразования);

-эти преобразования не указывают, как доопределять функцию, если функция неопределенна на всех наборах.

Вероятностные автоматы

Общие сведения о вероятностных автоматах

Вероятностные (стохастические) автоматы представляют собой конечные автоматы со случайными управлениями, у которых, как правило, учитываются только состояния.

Примером таких автоматов является модель системы, которая случайным образом может оказаться в одном из технических состояний (исправное, неисправное, поиск неисправности, ремонт и т.д.).

Можно сказать, что любая техническая система, если интересоваться не ее функционированием, а только техническими состояниями может быть представлена стохастическим конечным автоматом.

Изучением поведения стохастических автоматов занимается теория случайных процессов. Наиболее простыми и изученными процессами, проходящими в системах с дискретными состояниями, являются марковские процессы.

Марковские случайные процессы названы по имени выдающегося русского математика А.А.Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать "динамикой вероятностей". В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как: теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных научных областях.

Марковские цепи с дискретным временем

Марковским называется случайный процесс, состояние которого в очередной момент времени t + ∆t зависит только от текущего состояния в момент времени t. Это означает, что поведение марковского процесса в будущем определяется текущим состоянием процесса и не зависит от предыстории процесса – состояний, в которых пребывал процесс до момента t.

В классе марковских процессов выделяют процессы с дискретными состояниями, называемые марковскими цепями.

Когда множество состояний процесса S s1 ,...,sk конечно, марковскую цепь называют конечной.

Конечная марковская цепь может быть определена в дискретном или непрерывном времени.

В первом случае, переходы процесса из одного состояния в другое происходят только в фиксированные моменты времени, обозначаемые порядковыми номерами

56

t 0,1, 2,..., и цепь называется дискретной, во втором – переходы связываются с произвольными моментами времени t0 ,t1 ,t2 ,... и цепь называют непрерывной.

Основное отличие определяется целью исследования. Если важна только последовательность смены состояний, то процесс можно представить в виде дискретной марковской цепи, а если важно знать поведение в текущем времени, то в виде цепи с непрерывным временем.

Исходными данными для определения дискретной марковской цепи являются:

множество состояний S s1 ,...,sk ;

матрица вероятностей переходов (переходных вероятностей), характеризующей вероятности перехода процесса с текущим состоянием si в следующее состояние sj:

вектор		начальных		вероятностей	(начальное		распределение)
p	p(0)	,...p(0)	, определяющим вероятности p(0)			того,	что в начальный
0	1	k			i

момент времени t = 0 процесс находится в состоянии si.

Марковская цепь изображается в виде графа, вершины которого соответствуют состояниям цепи и дуги – переходам между состояниями.

Дуги (i, j), связывающие вершины st и s}, отличаются вероятностями переходов pij .

Например, на рис. 1.7.1 представлен граф марковской цепи с множеством состояний S s1 ,...,sk , матрицей вероятностей переходов:

и вектором начальных вероятностей p0 1,0, 0, 0, 0 .

57

s1 ,...sk

Рис. 1.7.1 Граф марковской цепи

Марковская цепь порождает множество реализаций случайного процесса f(t),

который	представляется					последовательностью	состояний		f (t) f0 , f1 , f2 ,...,
принадлежащих		множеству				состояний S s1 ,...,sk	и	соответствующих моментам
времени t = 0, 1, 2, ...
Начальное		состояние				f0 si определяется вектором		начальных	вероятностей .
Следующее состояние f			1	s	j	определяется i-й строкой матрицы вероятностей переходов

Р: процесс f(t) переходит в состояние f1 s j с вероятностью pij . Затем процесс переходит

в состояние f2 sk ,				определяемое вероятностями	p jk , соответствующими состоянию Sj, и
т.		д. В	результате	n шагов процесс попадает	в состояния s1 ,...,sk с вероятностями
p	n	p(n) ,...p(n) соответственно.
		1	k

Марковские цепи классифицируются в зависимости от возможности перехода из одних состояний в другие. Основными являются два класса: поглощающие и эргодические цепи.

Поглощающая марковская цепь содержит поглощающее состояние, достигнув которого, процесс уже никогда его не покидает, т. е. прекращается. Поглощающее состояние будем обозначать s0. Вероятность перехода p00 1 и, следовательно, все остальные вероятности p0 j 0 .

Матрица вероятностей переходов поглощающей цепи имеет следующий вид:

Из какого бы состояния ни начался процесс, при n→∞ с вероятностью 1 он окажется в поглощающем состоянии s0.

Основной характеристикой случайного процесса, порождаемого поглощающей марковской цепью является число пребываний процесса в состояниях до момента поглощения. Число пребываний в каждом из состояний si, на множестве невозвратных

58

состояний s1 ,...,sk являются случайными величинами, которые характеризуются средними

значениями, дисперсиями и распределениями. Для определения указанных характеристик используются методы алгебраической теории марковских цепей.

Поглощающие марковские цепи широко используются в качестве временных моделей программ и вычислительных процессов.

При моделировании программы состояния цепи отождествляются с блоками программы, а матрица переходных вероятностей определяет порядок переходов между блоками, зависящий от структуры программы и распределения исходных данных, значения которых влияют на развитие вычислительного процесса.

В результате представления программы поглощающей цепью удается вычислить число обращений к блокам программы и время выполнения программы, оцениваемое средними значениями, дисперсиями и при необходимости – распределениями. Аналогично вычислительный процесс, сводящийся к последовательности обращений к ресурсам системы в порядке, определяемом программой, можно представить поглощающей марковской цепью, состояния которой соответствуют использованию ресурсов системы, а переходные вероятности отображают порядок обращения к различным ресурсам. За счет этого вычислительный процесс представляется в компактной форме, удобной для анализа характеристик процесса.

Эргодическая марковская цепь представляет собой множество состояний, связанных матрицей переходных вероятностей таким образом, что из какого бы состояния процесс ни исходил, после некоторого числа шагов он может оказаться в любом состоянии (не содержит поглощающих состояний).

Это означает, что в любое состояние эргодической цепи можно перейти из любого другого состояния за конечное число шагов. По этой причине состояния эргодической цепи называются эргодическими (возвратными). Процесс, порождаемый эргодической цепью, начавшись в некотором состоянии, никогда не завершается, а последовательно переходит из одного состояния в другое, попадая в различные состояния с разной частотой, зависящей от переходных вероятностей.

Поэтому основными характеристиками эргодической цепи являются вероятности пребывания процесса в состояниях sj,, относительные частоты попадания процесса в эти состояния и доля времени, которую процесс проводит в каждом из состояний. В качестве дополнительных характеристик эргодических цепей могут использоваться математическое ожидание и дисперсия времени (числа шагов) первого попадания в состояние sj из состояния si.

Эргодические цепи широко используются в качестве моделей надежности систем. При этом состояния системы, различающиеся составом исправного и отказавшего оборудования, трактуются как состояния эргодической цепи, переходы между которыми связаны с отказами и восстановлением устройств и реконфигурацией связей между ними, проводимой для сохранения работоспособности системы. Оценки характеристик эргодической цепи дают представление о надежности поведения системы в целом. Кроме

59

pn

pn

того, эргодические цепи широко, используются в качестве базовых моделей взаимодействия устройств с задачами, поступающими на обработку.

Анализ марковских цепей

Результатом анализа марковской цепи являются ответы на два вопроса:

как при известном начальном состоянии от шага к шагу меняются вероятности состояний, в которых может находиться система,

каковы установившиеся значения этих вероятностей.

Покажем, как решается данная задача. Имеем вектор-строку pn p1(n) ,...pk(n) .

В начальный момент времени состояние известно: p0 1,0,...,0 .

Для расчета вероятностей используем уравнение Колмогорова-Чепмена:

pn 1 pn P ,

(1.7.1)

где Р - матрица вероятностей переходов.

С помощью уравнения Колмогорова-Чепмена можно вычислить вероятности состояний рекуррентно, т.е. последовательно:

p1 p0 P ,

p2 p1 P p0 P2 , p3 p2 P p0 P3 ,

…

pn pn 1 P p0 Pn .

При n→∞ можно определить установившиеся (финальные) вероятности. Для этого необходимо решить уравнение:

P ,

где pn ( p1 , p2 ...pk ) .

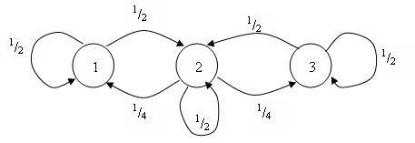
Пример 1. Вероятностный автомат представлен в виде графа, изображенного на рисунке 1.7.2.

				Рис. 1.7.2 Граф вероятностного автомата
		Требуется	определить, как меняется вектор вероятностей состояний
p	n	p(n) , p n , p(n) , если p		0	1,0,0 и чему равны финальные вероятности.
		1 2 3
					60