
моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем
.pdf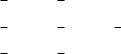
Решение. На основе графа (рис. 1.7.2) составим матрицу вероятностей:
|
|
|
1 |
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
P 4 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для определения векторов вероятностей состояний используем уравнение |
||||||||||||||||||||||
Колмогорова-Чепмена (1.7.1): |
|
|
|
|
|
|
||||||||||||||||
p p |
|
P (1,0,0) P ( |
1 |
, |
|
|
1 |
, 0) , |
||||||||||||||
0 |
|
|
|
2 |
||||||||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
p |
|
p P ( |
1 |
, |
1 |
, 0) P ( |
3 |
|
, |
|
1 |
, |
1 |
) , |
||||||||
2 |
|
|
8 |
2 |
|
|||||||||||||||||
|
|
|
1 |
|
|
|
2 |
2 |
|
|
|
|
|
8 |
|
|||||||
и т.д.
Для определения финальных вероятностей составим уравнение:
( p1 , p2 , p3 ) ( p1 , p2 , p3 ) P .
Это уравнение равносильно системе уравнений:
p( )
1
p2( )p3( )
12 p1( ) 14 p2( )
12 p1( ) 12 p2( ) 12 p3( )
14 p2( ) 12 p3( )
|
Для |
|
однозначного решения системы добавим |
|
нормирующую сумму |
||||||
p p p 1. Тогда из второго уравнения следует, что |
p( ) |
1 |
. |
||||||||
|
|||||||||||
1 |
2 |
3 |
|
|
|
2 |
2 |
|
|||
|
Значения остальных вероятностей очевидны: |
|
|
|
|
||||||
|
p( ) |
|
1 |
и |
p( ) |
1 |
. |
|
|
|
|
|
|
4 |
|
|
|
|
|||||
|
1 |
4 |
|
3 |
|
|
|
|
|
||
Марковские процессы
Понятие о марковских процессах с непрерывным временем переходов
Марковские процессы с непрерывным временем переходов можно рассматривать как марковские цепи, если разбить время на малые интервалы ∆t и определить вероятности pij за ∆t. При равных интервалах эти вероятности, для того, чтобы процесс был марковским, должны быть постоянными. В противном случае поведение будет зависеть от предыстории, в данном случае от того, как долго система находится в i-ом состоянии.
Вероятность pij при малых ∆t равна pij ij t , где ij - постоянный коэффициент, называемый интенсивностью перехода из i-го состояния в j-е состояние.
Возникает вопрос, какому закону распределения должно подчиняться время перехода?
В соответствии с марковским свойством вся предыстория процесса сказывается на его поведении в будущем только через текущее состояние, которое и определяет дальнейший ход процесса.
Таким образом, нет необходимости знать, как долго процесс находится в текущем состоянии. Отсюда следует, что распределение остающегося времени пребывания
61
процесса в состоянии sj должно зависеть только от самого состояния, а не от времени пребывания в нем. Этим свойством обладает только одно распределение – экспоненциальное.
Таким образом, непременное свойство непрерывного марковского процесса – экспоненциальность распределения времени пребывания процесса в каждом из состояний.
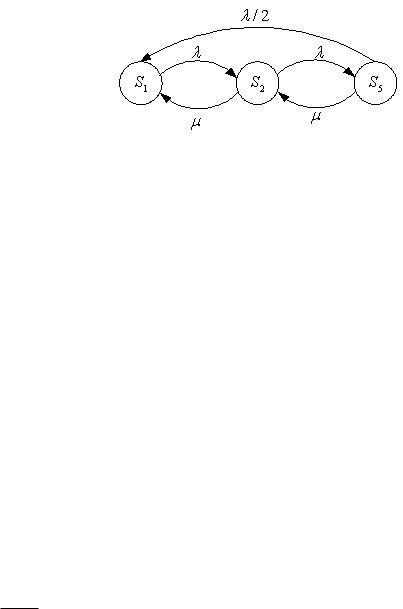
Марковский процесс с непрерывным временем переходов можно задать в виде графа (рис. 1.8.1) или описать системой дифференциальных уравнений.
Для определения финальных вероятностей состояний дифференциальные уравнения преобразуются в систему линейных уравнений.
Рис. 1.8.1 Граф марковского процесса
Иногда марковский процесс с дискретными состояниями, переходы между которыми разрешаются в любой момент времени, называется непрерывной марковской цепью.
Расчет характеристик марковских процессов
Рассмотрим, как можно получить дифференциальное уравнение, описывающее марковский процесс. Для этого используем уравнение Колмогорова-Чепмена (1.7.1.) в следующем виде:
P(t t) P(t) P .
Проведем следующие преобразования:
P(t t) P(t) P(t) P P(t) , |
|
|||
P(t t) P(t) |
|
P(t) (P E) |
|
, |
t |
|
t |
|
|
где Е – единичная матрица.
Тогда искомое дифференциальное уравнение в матричной форме примет следующий
вид:
|
|
P(t) P(t) A , |
(1.8.1) |
где A P E - матрица интенсивностей переходов.
t
Систему дифференциальных уравнений можно получить непосредственно из графа состояний. Например, имеем граф марковского процесса (рис. 1.8.2).
62
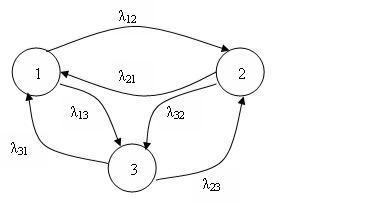
Рис. 1.8.2 Граф марковского процесса с тремя состояниями
Матрица вероятностей переходов для данного случая:
|
|
12 t |
13 t |
|
|
1 12 t 13 t |
|
||
P |
21 t |
1 21 t 23 t |
23 t |
. |
|
31 t |
32 t |
1 31 t 32 t |
|
В свою очередь матрица интенсивностей переходов имеет вид:
|
12 13 |
12 |
13 |
|
|
|
|||
A |
21 |
21 23 |
23 |
. |
|
31 |
32 |
31 32 |
|
На основе матричной записи дифференциального уравнения (1.8.1.) запишем систему уравнений:
P1 (t) ( 12 13 ) P1 (t) 21 P2 (t) 31 P3 (t)
P2 (t) 12 P1 (t) ( 21 23 ) P2 (t) 32 P3 (t)
P3 (t) 13 P1 (t) 23 P2 (t) ( 31 32 ) P3 (t)
Анализ полученной системы дает возможность сформулировать правило составления таких систем: для произвольного момента времени производная от вероятности i-го состояния равна сумме произведений всех других вероятностей на интенсивности перехода из них в i-ое состояние "минус" произведение вероятности i-го состояния на суммарную интенсивность выхода из i-го состояния.
Полученное правило можно записать в виде формулы:
|
Pj (t) Pi (t) ij . |
Pi (t) ij |
|
j |
j |
Для установившегося режима Pi (t) 0 и система дифференциальных уравнений преобразуется к системе линейных алгебраических уравнений, решением которой являются финальные вероятности состояний системы. Определение финальных вероятностей рассмотрим на примере.
Пример. Система может находиться в двух состояниях. Для описания модели системы составим граф марковского процесса (рис.1.8.3).
63

Рис. 1.8.3 Граф марковского процесса с двумя состояниями
Требуется определить финальные значения вероятностей состояний P1 (t) , P2 (t) . Решение.
Для определения вероятностей составим систему дифференциальных уравнений:
|
(t) P (t) |
|
|
|
P (t) |
|
|
|
||||
P1 |
21 |
|
|
|
||||||||
|
|
12 |
1 |
|
|
|
2 |
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) P (t) |
|
|
|
P (t) |
|
|
|
|||||
P2 |
21 |
|
|
|
||||||||
|
|
12 |
1 |
|
|
2 |
|
|
|
|||
Чтобы получить финальные значения вероятностей необходимо перейти к |
||||||||||||
алгебраическим уравнениям: |
|
|
|
|||||||||
0 12 P1 21 P2 |
|
|
|
|
|
|
|
|
||||
0 12 P1 21 P2 |
|
|
|
|
|
|
|
|
||||
После замены |
любого уравнения на нормирующую сумму |
P P 1 |
решение |
|||||||||
1 2 |
||||||||||||
системы становится очевидным: |
|
|
||||||||||
P1 |
|
21 |
, P2 |
|
|
|
|
|
12 |
. |
|
|
12 21 |
|
12 21 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
Модель "гибели и размножения"
Схема "гибели и размножения" часто встречается в разнообразных практических задачах. Своим названием эти процессы обязаны биологической задаче об изменении численности популяции и распространением эпидемий.
В технических системах данной моделью описывают процессы возникновения отказа и восстановления.
Процесс "гибели и размножения" может быть представлен марковским случайным процессом с непрерывным временем, причем число состояний может быть бесконечным или конечным. В этом случае интервалы времени между двумя моментами рождения и гибели распределены по экспоненциальному закону.
Таким образом, марковский процесс называется процессом "гибели и размножения", если его граф состояний (рис. 1.8.4) имеет вид цепочки состояний, в которой каждое состояние (кроме крайних) связано с двумя соседними состояниями, а крайние состояния только с соседним состоянием.
Рис. 1.8.4 Схема "гибели и размножения"
64
Для такого графа достаточно просто определяются финальные вероятности
состояний. Действительно |
|
|
|
|
|
|
|
|||||
01P0 10 P1 - для нулевого состояния, |
|
|
||||||||||
( |
|
)P |
01 |
P |
21 |
P |
P |
21 |
P - для первого состояния, и т.д. |
|||
12 |
10 |
1 |
0 |
2 |
12 |
1 |
2 |
|
|
|||
n 1, n Pn 1 n, m 1Pn - для последнего состояния. |
|
|||||||||||
В итоге получилась система уравнений. |
|
|
||||||||||
Добавим к ней нормировочное уравнение |
P P P ... P 1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 1 2 |
n |
Вероятность всех состояний выразим через вероятность нулевого состояния:
P |
01 P |
, |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
P |
12 P |
01 12 P |
, |
|
|||
2 |
1 |
|
|
0 |
|
|
|
|
21 |
|
21 10 |
|
|
||
… |
|
|
|
|
|
|
|
P |
n 1, n P |
|
01 12... n 1, n |
P |
|||
n |
n, n 1 |
n 1 |
|
n, n 1... 21 10 |
0 |
||
|
|
|
|
|
|||
После подстановки вероятностей в нормировочное уравнение выражение для определения вероятности нулевого состояния примет следующий вид:
P0 |
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|||
|
01 |
|
01 12 |
|
|
|||
1 |
|
.. |
01 12... n 1, n |
|
||||
|
|
n, n 1... 21 10 |
||||||
|
|
10 |
21 10 |
|
||||
Значения остальных вероятностей рассчитываются по полученным ранее соотношениям.
Модели массового обслуживания
Области применения. Основные понятия
В задачах автоматизированного управления, особенно в задачах организованного управления, часто приходится иметь дело с объектами, которые заняты обслуживанием поступающих в общем случае случайных потоков заявок или требований.
На первое место выдвигаются такие характеристики этого процесса, как время обслуживания, время нахождения заявок в системе, длина очереди и т.п.
Например: ремонтный орган, ателье, телефонный канал или АТС в целом, библиотека, медпункт, сбербанк, магазин, аэродром, процессор, память (в том числе и жесткий диск), поток отказов РЭА и т.д.
Для описания процессов в таких системах и получения характеристик разработана теория массового обслуживания. Построение модели массового обслуживания и расчет характеристик требует знания распределения времени между заявками и распределение времени обслуживания.
65

Потоком событий называется последовательность однородных событий, следующих одно за другим в какой-то случайный момент времени.
Поток событий можно наглядно изобразить рядом точек на оси времени (рис.1.9.1).
Рис. 1.9.1 Изображение потока событий на оси времени
Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока.
Говоря о «потоке событий», нужно иметь в виду, что здесь термин «событие» имеет значение, несколько отличное от того, к которому мы привыкли в теории вероятностей. Там «событием» (или «случайным событием») называется какой-то исход опыта, обладающий той или другой вероятностью. События, образующие поток, сами по себе вероятностями не обладают; вероятностями обладают другие, производные от них события, например: «на участок времени 2 (рис. 1.9.1) попадает ровно два события», или «на участок времени t попадает хотя бы одно событие», или «промежуток времени между двумя соседними событиями будет меньше t».
Важной характеристикой потока событий является его интенсивность — среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной ( = const), так и переменной, зависящей от времени t. Например, поток автомашин, движущихся по улице, днем интенсивнее, чем ночью, в часы пик — интенсивнее, чем в другие часы.
Поток событий называется регулярным, если события следуют одно за другим через определенные, равные промежутки времени. На практике чаще встречаются потоки нерегулярные, со случайными интервалами.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока должна быть постоянной. Это отнюдь не значит, что фактическое число событий, появляющееся в единицу времени, постоянно, - нет, поток неизбежно (если только он не регулярный) имеет какие-то случайные сгущения и разрежения, как, например, показано на рис. 1.9.1. Важно, что для стационарного потока эти сгущения и разрежения не носят закономерного характера: на один участок длины 1 может попасть больше, а на другой – меньше событий, но среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
Поток событий называется потоком без последействия, если для любых двух непересекающихся интервалов времени 1 и 2 (рис. 1.9.1) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. По сути, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, причем каждое вызвано своими собственными причинами.
66
Например, поток пассажиров, входящих в метро, практически не имеет последействия. А вот поток покупателей, отходящих от прилавка с купленными товарами, уже имеет последействие (хотя бы потому, что интервал времени между отдельными покупателями не может быть меньше, чем минимальное время t0 обслуживания каждого из них).
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами. Например, поток клиентов, направляющихся в парикмахерскую или к зубному врачу, обычно ординарен, чего нельзя сказать о потоке клиентов, направляющихся в загс для регистрации брака. Поток поездов, подходящих к станции, ординарен, а поток вагонов — неординарен. Если поток событий ординарен, то вероятностью попадания на малый интервал времени t двух или более событий можно пренебречь.
Простейший поток заявок
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия. Название «простейший» связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание. Самый простой, на первый взгляд, регулярный поток не является «простейшим», так как обладает последействием: моменты появления событий в таком потоке связаны жесткой функциональной зависимостью. Без специальных усилий по поддержанию его регулярности такой поток обычно не создается.
Простейший поток играет среди других потоков особую роль. А именно, при наложении (суперпозиции) достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.
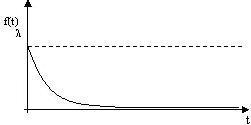
Для простейшего потока с интенсивностью интервал между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью
f (t) e t |
(t > 0) |
(1) |
, |
где - параметр показательного закона
Рис. 1.9.2 График плотности распределения экспоненциального распределения
Для случайной величины Т, имеющей экспоненциальное распределение, математическое ожидание mT есть величина, обратная параметру, а среднее квадратическое отклонение T равно математическому ожиданию:
mT |
T |
1/ |
(2) |
|
|
|
|
|
|
|
67 |
В теории вероятностей в качестве «меры случайности» неотрицательной случайной величины нередко рассматривают так называемый коэффициент вариации:
(3)
Из формул (2), (3) следует, что для показательного распределения t = 1, т. е. для простейшего потока событий коэффициент вариации интервалов между событиями равен единице.
Очевидно, что для регулярного потока событий, у которого интервал между событиями вообще не случаен ( t = 0), коэффициент вариации равен нулю. Для большинства потоков событий, встречающихся на практике, коэффициент вариации интервалов между событиями заключен между нулем и единицей и может служить некоторой мерой «степени регулярности» потока: чем ближе t к нулю, тем «регулярнее» поток. Простейший поток – это «наименее регулярный» из встречающихся на практике потоков.
В расчетах, связанных с потоками событий, очень удобно пользоваться понятием «элемента вероятности». Рассмотрим на временной оси простейший поток с интенсивностью и произвольно расположенный элементарный (очень маленький) участок времени t.
Элементом вероятности называется вероятность попадания на этот интервал хотя бы одного события потока. Легко доказать, что элемент вероятности (с точностью до малых величин более высокого порядка по сравнению с t) равен:
p t t , (4)
т. е. для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного интервала. Элемент вероятности, в силу отсутствия последействия, совершенно не зависит от того, сколько событий и когда появлялись ранее.
Рекуррентные потоки. Формула Литтла
Поток событий называется рекуррентным (иначе – «потоком «Пальма»), если он стационарен, ординарен, а интервалы времени между событиями T1, T2, T3, … представляют собой независимые случайные величины с одинаковым произвольным распределением. Приведем пример рекуррентного потока. Технический элемент (например, диод) работает непрерывно до своего отказа (выхода из строя); отказавший элемент мгновенно заменяется новым. Если отдельные экземпляры элемента выходят из строя независимо друг от друга, то поток отказов (он же «поток замен» или «восстановлений») будет рекуррентным.
Рассмотрим вывод упомянутой ранее формулы Литтла, связывающей (для предельного, стационарного режима) среднее число заявок Lсист, находящихся в системе массового обслуживания (т. е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе Wсист.
68

Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее, так как оба потока имеют одну в ту же интенсивность .
Обозначим: X(t)—число заявок, прибывших в СМО до момента t, Y(t) — число заявок, покинувших СМО до момента t. И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (Y(t)). Для любого момента t их разность Z(t) = X(t) - Y(t) — это число заявок, находящихся в СМО.
Рассмотрим очень большой промежуток времени T и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала T:
Z (t)dt
(5)
Данный интеграл представляет собой площадь фигуры, заключенной между X(t) и Y(t). Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена как t1, t2,... Правда, под конец промежутка Т некоторые прямоугольники войдут в эту фигуру не полностью, а частично, но при достаточно большом Т этим можно пренебречь. Таким образом, можно считать, что
T
Z (t)dt ti
0 |
i |
, |
(6) |
|
|
где сумма распространяется на все заявки, пришедшие за время Т.
Разделим правую и левую часть (6) на длину интервала Т. Получим, с учетом (5):
LС И СТ |
1 |
ti |
|
|
|||
|
|
|
|||||
|
T |
i |
. |
(7) |
|||
|
|
|
|
|
|||
Разделим и умножим правую часть (7) на интенсивность : |
|||||||
LС И СТ |
1 |
ti |
|
||||
T |
(8) |
||||||
|
i |
|
|||||
|
|
|
|
|
|
||
Величина T — это среднее число заявок, пришедших за время Т. Если мы разделим |
|||||||
сумму всех времен ti |
на среднее число заявок, то получим среднее время пребывания |
||||||
заявки в системе Wсист. Итак, |
|||||||
LСИСТ WСИСТ . |
(9) |
||||||
Это и есть формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания
69
среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.
Точно таким же образом выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди Wоч и среднее число заявок в очереди Lоч.
LОЧ WОЧ . |
(10) |
Системы массового обслуживания и их характеристики
При исследовании операций часто приходится сталкиваться с работой систем массового обслуживания. СМО могут быть одноканальными и многоканальными.
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (прихода новой заявки, окончания обслуживания, момента, когда заявка, которой «надоело ждать», покидает очередь).
Предмет теории массового обслуживания — построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками — показателями эффективности СМО, описывающими, с той или другой точки зрения, ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение, простои, и т. д.
Математический анализ работы СМО очень упрощается, если процесс этой работы
—марковский. Для этого достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние (потоки заявок, «потоки обслуживания»), были простейшими. Если это свойство нарушается, то математическое описание процесса становится гораздо сложнее и довести его до явных, аналитических формул удается лишь в редких случаях. Однако аппарат простейшей, марковской теории массового обслуживания может пригодиться для приближенного описания работы СМО даже в тех ситуациях, когда потоки событий — не простейшие. Во многих случаях для принятия разумного решения по организации работы СМО вовсе и не требуется точного знания всех ее характеристик
—зачастую достаточно и приближенного, ориентировочного.
Системы массового обслуживания делятся на типы (или классы) по ряду признаков. Первое деление: СМО с отказами и СМО с очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует. Примеры СМО с отказами встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы связи заняты, получает отказ и покидает СМО необслуженной. В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. На практике чаще встречаются (и имеют
70
