моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

большее значение) СМО с очередью; недаром теория массового обслуживания имеет второе название: «теория очередей».

СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь — ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания»

— заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке. Нередко встречается так называемое обслуживание с приоритетом — некоторые заявки обслуживаются вне очереди. Приоритет может быть как абсолютным — когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим, так и относительным — когда начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди.

Существуют СМО с так называемым многофазовым обслуживанием, состоящим из нескольких последовательных этапов или «фаз» (например, покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, после чего получить на контроле).

Кроме этих признаков, СМО делятся на два класса: «открытые» и «замкнутые». В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии находится сама СМО (сколько каналов занято). В замкнутой СМО — зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки. Это — пример замкнутой СМО.

n-канальная система с отказами

Это одна из первых задач теории массового обслуживания. Она возникла из практических нужд телефонии и была решена в начале 20 века датским математиком Эрлангом.

Дано: в системе имеется n – каналов, на которые поступает поток заявок с интенсивностью . Поток обслуживаний имеет интенсивность . Заявка, заставшая систему занятой, сразу же покидает ее.

Найти: финальные вероятности состояний СМО pn, а также характеристики ее эффективности:

A - абсолютную пропускную способность, т.е. среднее число заявок, обслуживаемых в единицу времени;

Q - относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

PОТК - вероятность отказа, т.е. того, что заявка, пришедшая в момент времени t, получит отказ;

k - среднее число заявок, обслуживаемых одновременно (или, другими словам, среднее число занятых каналов).

71

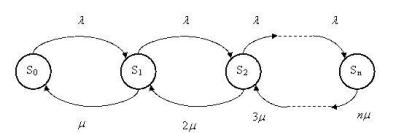
Решение. Состояние системы S (СМО) нумеруется по максимальному числу заявок, находящихся в системе (оно совпадает с числом занятых каналов):

-S0 – в СМО нет ни одной заявки;

-S1 – в СМО находится одна заявка (один канал занят, остальные свободны);

-S2 – в СМО находится две заявки (два канала заняты, остальные свободны);

-Sk – в СМО находится k заявок (k каналов заняты, остальные свободны);

…

-Sn – в СМО находится n – заявок (все n – каналов заняты).

Граф состояний СМО представлен на рисунке 1.10.1.

Рис. 1.10.1 Граф состояний для n – канальной СМО с отказами

Используя формулы для финальных вероятностей в схеме гибели и размножения,

учитывая, что 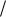, получаем:

2

k

n 1

p0 1

...

...

2!

k!

n!

;

p1

2

p0 , … ,

p1 p0 ,

2!

pk

k

n

p0

, …,

pn

p0

.

k!

n!

(11)

(12)

Эти формулы для финальных вероятностей состояний называются формулами Эрланга – в честь основателя теории массового обслуживания.

Зная финальные вероятности, нетрудно вычислить характеристики эффективности СМО, в частности, вероятность отказа:

	pn	n
P			p0
ОТК		n! .				(13)
Отсюда находим относительную пропускную способность:
Q 1 P		1		n	p0
	ОТК			n!	.	(14)

Абсолютную пропускную способность находим, умножая интенсивность потока заявок на Q:

72

		n
A Q 1			p0
		n!
				.

Среднее число занятых каналов определяется как:

		n
k A / 1			p0
		n!
				.

Одноканальная СМО с неограниченной очередью

(15)

(16)

На практике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов, процессор, выполняющий машинные команды). Поэтому необходимо рассмотреть одноканальные СМО с очередью более подробно.

Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На эту СМО поступает поток заявок с интенсивностью ; поток обслуживаний имеет интенсивность , обратную среднему времени обслуживания заявки tоб. Требуется найти финальные вероятности состояний СМО, а также характеристики ее эффективности:

LСИСТ – среднее число заявок в систем;

WСИСТ – среднее время пребывания заявки в системе; LОЧ – среднее число заявок в очереди;

WОЧ – среднее время пребывания заявки в очереди;

PЗАН — вероятность того, что канал занят (степень загрузки канала).

Что касается абсолютной пропускной способности A и относительной Q, то вычислять их нет необходимости: в силу того, что очередь неограниченна, каждая заявка

рано или поздно будет обслужена, поэтому A , по той же причине Q 1.

Решение. Состояние системы, как и раньше, будем нумеровать по числу заявок, находящихся в СМО:

-S0 – канал свободен;

-S1 – канал занят (обслуживает заявку), очереди нет;

-S2 – канал занят, одна заявка стоит в очереди;

…

- Sk – канал занят, k-1 заявок стоят в очереди.

Теоретически число состояний ничем не ограничено (бесконечно). Формулы для финальных вероятностей в схеме гибели и размножения выводились только для случая конечного числа состояний, но сделаем допущение – воспользуемся ими и для бесконечного числа состояний. Тогда число слагаемых в формуле будет бесконечным. Получим выражение для pо:

1	1 .
p0 1 2 ... k ...		(17)
Ряд в формуле (17) представляет собой геометрическую прогрессию. Мы знаем, что

при 1	ряд сходится – это бесконечно убывающая прогрессия со знаменателем . При
	73

1 ряд расходится (что является косвенным, хотя и не строгим доказательством того,

что финальные вероятности состояний pо, p1, …, pk,… существуют только при 1). Тогда:

р (1 )	,	р	2	2	(1 )	,…,	р	k	k (1 )	(18)
1

Найдем среднее число заявок в СМО LСИСТ. Случайная величина Z – число заявок в системе – имеет возможные значения 0, 1, 2, …, k, … с вероятностями pо, p1, …, pk,… Ее математическое ожидание равно:

L			k pk 1 d			k
	СИСТ
				d			1
			k 1		k 1			;	(19)

Применяя формулу Литтла (9), найдем среднее время пребывания заявки в системе:

WСИСТ 1	;	(20)

Найдем среднее число заявок в очереди. Будем рассуждать так: число заявок в очереди равно числу заявок в системе минус число заявок, находящихся под обслуживанием. Значит (по правилу сложения математических ожиданий) среднее число заявок в очереди LОЧ равно среднему числу заявок в системе LСИСТ минус среднее число заявок под обслуживанием. Число заявок под обслуживанием может быть либо нулем (если канал свободен), либо единицей (если он занят). Математическое ожидание такой случайной величины равно вероятности того, что канал занят PЗАН. Очевидно, что:

PЗА Н	1 p0		.					(21)
Следовательно, средне число заявок под обслуживанием равно:
LОБ		,						(22)
отсюда
LОЧ	LСИСТ					2
						.
			1					(23)
По формуле Литтла (9) найдем среднее время пребывания заявки в очереди:
WОЧ		2
		(1 ) .						(24)

n-канальная СМО с неограниченной очередью

Аналогично предыдущей задаче, решается задача об n-канальной СМО с неограниченной очередью. Нумерация состояний – опять по числу заявок, находящихся в системе:

-S0 – в СМО нет ни одной заявки (все каналы свободны);

-S1 – занят один канал, остальные свободны;

-S2 – занято два канала заняты, остальные свободны;

…

74

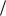
-Sk – занято k каналов, остальные свободны;

…

-Sn – заняты все n каналов (очереди нет);

-Sn+1 – заняты все n каналов, одна заявка стоит в очереди;

…

-Sn+r – заняты все n каналов, r заявок стоит в очереди;

…

Условие существования финальных вероятностей: 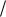n 1, в противном случае,

очередь растет до бесконечности.

Применяя формулы для схемы гибели и размножения, найдем финальные вероятности:

				2	n		n 1	1
p	1			...
	0	1! 2!			n!		n! n		(25)
								,

k

n

n r

pk k!

p0 ,

pn n!

p0 ,

pn r nr n! p0 .

(26)

Теперь найдем характеристики эффективности СМО. Из них легче всего найти

среднее число занятых каналов k

(это вообще справедливо для любой СМО с

неограниченной очередью). Найдем среднее число заявок в очереди LОЧ:

LОЧ

n 1 p

0

n n! 1 / n 2

.

(27)

Прибавляя к нему среднее число заявок под обслуживанием (оно же – среднее число

занятых каналов), получим:

LСИСТ LОЧ

.

(28)

Деля выражения LОЧ и LСИСТ на , по формуле Литтла получим средние времена

пребывания заявок в очереди и в системе:

W

1

L

W

1

L

ОЧ

ОЧ

СИСТ

СИСТ

,

.

(29)

Более сложные задачи теории массового обслуживания

Здесь мы рассмотрим вопросы, относящиеся к немарковским СМО. До этого все формулы выводились на основе схемы гибели и размножения, формулы Литтла и дифференцирования.

До сих пор рассматривались только простейшие СМО, для которых все потоки событий, перевод их из состояния в состояние, были простейшими. Для немарковских СМО существуют только отдельные, считанные результаты, позволяющие выразить в явном, аналитическом виде характеристики СМО через заданные условия задачи – число

75

каналов, характер потока заявок, распределения времен обслуживания. Рассмотрим некоторые результаты.

n-канальная СМО с отказами, с простейшим потоком заявок и произвольным распределением времени обслуживания.

Формулы 11 и 12, полученные в 1.10.1 для финальных вероятностей состояний СМО с отказами, справедливы не только при показательном, но и при произвольном распределении времени обслуживания. Это доказал Б.А.Севастьянов в 1959г.

Одноканальная СМО с неограниченной очередью, простейшим потоком заявок и произвольным распределением времени обслуживания.

Если на одноканальную СМО с неограниченной очередью поступает простейший поток заявок с интенсивностью , а время обслуживания имеет произвольное

									об 1
распределение с математическим ожиданием t										и коэффициентом вариации , то
среднее число заявок в очереди равно:
		2 1 2
LОЧ
	2 1		,							(30)
а среднее число заявок в системе
		2 1 2
LСИСТ
		2 1
							,			(31)
где, как и ранее			, а - отношение среднеквадратического отклонения времени

обслуживания к его математическому ожиданию. Формулы (30, 31) носят название формул Полячека – Хинчина.

Деля LОЧ и LСИСТ на , получим, согласно формуле Литтла, среднее время пребывания заявки в очереди и среднее время пребывания в системе:

		2 1 2
WОЧ
	2 1		,					(32)
		2 1 2
WСИСТ							1/
		2 1
							.	(33)

Заметим, что в частном случае, когда время обслуживания – показательное, = 1 и формулы 30, 31 превращаются в уже знакомые формулы для простейшей одноканальной СМО (19, 23).

Одноканальная СМО с произвольным потоком заявок и произвольным распределением времени обслуживания.

Рассматривается одноканальная СМО с неограниченной очередью, на которую поступает произвольный рекуррентный поток заявок с интенсивностью и коэффициентом вариации интервалов между заявками, заключенных между нулем и единицей. Время обслуживания Tоб также имеет произвольное распределение со средним

значением tоб 1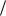 и коэффициентом вариации , тоже заключенным между нулем и

76

единицей. Для этого случая точных аналитических формул получить не удается, можно только приближенно оценить среднюю длину очереди, ограничить ее сверху и снизу.

Доказано, что в этом случае

2 2		2					1 2				2 2	2					1 1 2
									LОЧ
2 1							2				2 1						2	(34)

Если входящий поток – простейший, то обе оценки – верхняя и нижняя – совпадают, и получается формула Полячека-Хинчина (30). Для грубо приближенной оценки средней длины очереди М.А.Файнбергом получена простая формула:

		2 2	2
LОЧ
		2 1			.

Среднее число заявок в системе получается из LОЧ простым прибавлением - среднего числа обслуживаемых заявок:

LСИСТ LОЧ .

Что касается средних времен пребывания заявки в очереди и в системе, то они вычисляются через LОЧ и LСИСТ по формуле Литтла делением на .

Таким образом, характеристики одноканальных СМО с неограниченной очередью могут быть (если не точно, то приближенно) найдены и в случаях, когда потоки заявок и обслуживаний не являются простейшими.

Возникает естественный вопрос: а как же обстоят дело с многоканальными немарковскими СМО?

Точных аналитических методов для таких систем не существует. Единственное, что

всегда можно найти, это среднее число занятых каналов k . Что касается LОЧ, LСИСТ, WОЧ, WСИСТ, то для них таких общих формул написать не удается.

Правда, если каналов действительно мало (4-5 или больше), то непоказательное время обслуживания не так важно: был бы поток простейшим. Действительно, общий поток «освобождений» каналов складывается из потоков освобождений отдельных каналов, а в результате такого наложения («суперпозиции») получается, поток, близкий к простейшему. Так что в этом случае замена непоказательного распределения времени обслуживания показательным приводит к сравнительно малым ошибкам. Обычно входной поток заявок во многих задачах практически близок к простейшему.

Значительно хуже, если входной поток заведомо не простейший. В этом случае необходимо подобрать две одноканальные СМО, из которых одна по своей эффективности заведомо «лучше» данной многоканальной, а другая – заведомо «хуже» (очередь больше, время ожидания больше). Таким образом, получая характеристики одноканальной СМО на основе известных, рассмотренных нами, способов, можно получить «оптимистические» и «пессимистические» оценки характеристик эффективности рассматриваемой СМО.

77

Раздел 2. Компьютерное моделирование

Теоретические занятия (лекции) – 6 часов

Лекция 4. Статистическое моделирование

В этой лекции излагаются сущность и основные аспекты имитационного моделирования: моделирования случайных величин, событий и процессов.

Статистическое моделирование на ЭВМ

Компьютерное моделирование существует с тех пор, когда появились первые компьютеры и исследователи стали перекладывать на них трудоемкие операции.

Как новый метод научных исследований компьютерное моделирование основывается на построении математических моделей для описания изучаемых процессов и использовании новейших вычислительных машин, обладающих высоким быстродействием, способных вести диалог с человеком.

Можно дать такое определение компьютерному моделированию: это деятельность по разработке программных моделей систем, выполнение этих программ на компьютере и анализ результатов по исследованию поведения моделей.

Отмечают две области компьютерного моделирования – имитационное и статистическое моделирование.

Имитационное моделирование представляет собой численный метод проведения на ЭВМ вычислительных экспериментов с математическими моделями, имитирующими поведение реальных объектов, процессов и систем во времени в течение заданного периода. При этом их функционирование разбивается на элементарные явления, подсистемы и модули. Функционирование этих элементарных явлений, подсистем и модулей описывается набором алгоритмов, которые имитируют элементарные явления с сохранением их логической структуры и последовательности протекания во времени. В настоящее время широко применяются готовые программные продукты для моделирования различного рода систем: GPSS, VisSim, AnyLogic, DyMoLa, Dynast,

Multisim, MBTY, Simulink и другие.

Одним из видов имитационного моделирования является статистическое имитационное моделирование, позволяющее воспроизводить на ЭВМ функционирование сложных случайных процессов.

В вероятностном имитационном моделировании оперируют не с характеристиками случайных процессов, а с конкретными случайными числовыми значениями параметров системы. При этом результаты, полученные при воспроизведении на имитационной модели рассматриваемого процесса, являются случайными реализациями. Поэтому для нахождения объективных и устойчивых характеристик процесса требуется его многократное воспроизведение, с последующей статистической обработкой полученных данных. Именно поэтому исследование сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационного моделирования принято называть статистическим моделированием.

78

Статистическая модель случайного процесса - это алгоритм, с помощью которого имитируют работу сложной системы, подверженной случайным возмущениям; имитируют взаимодействие элементов системы, носящих вероятностный характер.

Применение статистического моделирования широко распространено в задачах анализа и проектирования автоматизированных систем, информационно-вычислительных сетей и других сложных организационно-технических объектов. При реализации статистического имитационного моделирования возникает задача получения случайных числовых последовательностей с заданными вероятностными характеристиками.

Таким образом, статистическое моделирование – это метод решения вероятностных и детерминированных задач, основанный на эффективном использовании случайных чисел и законов теории вероятностей.

Этот метод использует способность современных компьютеров порождать и обрабатывать за короткие промежутки времени значительное количество случайных чисел.

Организация статистического моделирования

Подавая последовательность случайных чисел на вход исследуемой модели, на еѐ выходе получают преобразованную последовательность случайных величин – выборку.

При правильной организации подобного статистического эксперимента выборка содержит ценную информацию об исследуемой модели, которую трудно или практически невозможно получить другими способами.

Информация извлекается из выборки методами математической статистики.

Метод статистического моделирования (другое его название – метод Монте-Карло) позволяет, опираясь на законы теории вероятностей, свести широкий класс сложных задач к относительно простым арифметико-логическим преобразованиям выборок. Поэтому такой метод и получил весьма широкое распространение. В частности, он почти всегда используется при имитационном моделировании реальных сложных систем.

При реализации на ЭВМ статистического моделирования возникает задача получения (генерирования) на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками, в которых каждое число – это имитация случайного значения какого-либо параметра реального процесса или системы, подверженного случайным возмущениям.

Таким образом, при имитационном моделировании стохастических систем приходится имитировать

случайное событие с заданными вероятностями,

случайные величины с заданными распределениями,

случайные процессы с заданными характеристиками (математическое ожидание, дисперсия, корреляционная функция).

Для имитации случайной величины с заданным распределением нужно иметь генератор (датчик) случайных чисел (ДСЧ), генерирующий числа с заданным законом

79

распределения. Оказывается, что достаточно для любого распределения иметь генератор равномерно распределенной величины в интервале от 0 до 1, в противном случае необходимо было бы для каждого распределения строить свой генератор.

Задачу генерирования случайных чисел на ЭВМ с заданным законом распределения решают в два этапа.

Вначале получают последовательность равномерно распределенных на интервале [0, 1] псевдослучайных чисел, а затем из равномерно распределенной последовательности получают последовательность псевдослучайных чисел с заданным законом распределения в заданном интервале. Подробнее об этом будет рассказано в следующей лекции.

Генерирование базового распределения

Датчики случайных чисел могут быть трех типов: табличные, физические и программные.

Табличный датчик – это просто таблица случайных чисел. Основной недостаток такого датчика – ограниченное количество случайных чисел в таблицах, а в статистическом эксперименте часто требуется не ограниченное заранее их количество.

Физический датчик – это специальное радиоэлектронное устройство, содержащее источник электронного шума. Шум преобразуется в случайные числа с распределением.

В качестве генератора случайностей ранее использовались физические датчики, работа которых основана на излучении радиоактивных веществ и на собственных шумах электрических ламп. В первом случае подсчитывалось число радиоактивных веществ заt, если оно четное, то случайная величина равна 0, если нечетное – 1. Во втором – в датчиках шум сравнивался с порогом в течении t, если шум превышает порог, то случайная величина равна 1, в противном случае – 0.

Недостатки физического датчика: невозможность повторения каких-либо ранее полученных реализаций z1, ... , zn без их предварительной записи в память ЭВМ, схемная нестабильность и сложность тиражирования датчика.

Поэтому, в настоящее время используют не физические, а программные датчики, которые генерируют псевдослучайные числа, идущие в строго определенной последовательности.

Сущность алгоритмических методов получения равномерно распределенных псевдослучайных чисел заключается в том, что псевдослучайные числа получают с помощью некоторой рекуррентной формулы xi 1 f (xi ) , где каждое следующее (i+1)

значение образуется из предыдущего (или группы предыдущих) путем применения некоторого алгоритма, содержащего логические и арифметические операции.

Метод середины квадрата

Первый алгоритм для получения псевдослучайных чисел был предложен Нейманом в 1946 г. Алгоритм, получивший название "метод середины квадрата", состоит в том, что

80