моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

произвольное число, меньшее 1 возводят в квадрат, затем отбрасывают цифры с обоих концов, а оставшуюся часть используют как случайное число. Далее процесс повторяют.

Например,

x	0	0,2601	x2	0,04 2477 21
			0
x		0,2477	x2	0,06 1355 29
1			1
x	2	0,1355	x2	0,01 8360 25
			2

и т.д.

Мультипликативный конгруэнтный метод

Наиболее современный способ получения равномерно распределенных случайных чисел чi заключается в расчете по формуле:

xi 1 (axi ) mod m,

где mod – операция получения остатка от деления axi на m; a и m – задаваемые целые числа;

x0 – задается в начале расчета алгоритма.

В результате получим случайное число чi mxi .

Пары чисел a и m должны быть тщательно подобраны, так как от них зависит период псевдослучайной последовательности. Известны наиболее оптимальные пары:

a 8192 213 , m 67101.323 226 .

m 231 1, a 75 .

Заметим, однако, что в настоящее время не известны правила, которые гарантировали бы высокое качество датчика без его специального статистического тестирования.

Существуют также генераторы, построенные по более общей формуле xi 1 axi c mod m , здесь уже три параметра: целые числа a, m и c.

Последовательность, полученная из последнего соотношения, называется линейной конгруэнтной последовательностью.

Метод получения случайных чисел при c = 0 называется мультипликативным конгруэнтным методом, а при с ≠ 0 - смешанным конгруэнтным методом. При c = 0, выработка последовательностей происходит быстрее, но при этом уменьшается длина периода последовательностей.

Датчик называют мультипликативно-конгруэнтным потому, что он использует две основные операции – умножение (англ. multiplication) и вычисление остатка (в теории чисел – получение конгруэнтного числа).

Выражения, по которым определяются случайные числа, позволяют оценить периодичность псевдослучайной последовательности. В теории чисел доказано, что период псевдослучайной последовательности равен m, если m 2 p , a 2b 1 b 2 , c - нечетное.

81

Линейные конгруэнтные последовательности – не единственные из предложенных источников случайных чисел. Его можно обобщить, превратив его, например, в квадратичный конгруэнтный метод xi 1 dxi2 axi c mod m .

Проверка качества датчика случайных чисел

Поскольку псевдослучайная последовательность строится по эмпирическим формулам, то обязательно необходимо проверять требования, которым должен удовлетворять датчик случайных чисел (ДСЧ).

Основные требования, предъявляемые к ДСЧ:

1.Равномерность распределения псевдослучайных чисел.

2.Независимость чисел.

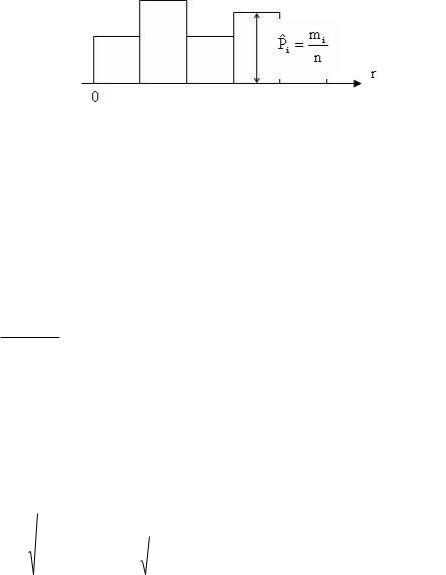
Равномерность можно проверить визуально по гистограмме (рис. 2.1.1).

Рис. 2.1.1 Гистограмма

где mi – количество чисел, попавших в i-ый интервал; n – общее число чисел.

Высота столбиков пропорциональна частотам попадания чисел в интервалы. При большом значении n столбики должны выравниваться.

Более точное заключение о равномерности можно сделать с учетом числа опытов. Известно, что дисперсия оценки вероятности события при n опытах и биномиальной схеме испытаний (да - нет) равна

D P

ˆ P 1 P ,

n

где P – истинное значение вероятности события.

В действительности оценка может отличаться от истинного значения на 3 (‗три сигма‘). Если число интервалов гистограммы равно m и распределение действительно равномерное, то истинное значение вероятности события должно равняться 1/m.

Таким образом, если высота столбиков гистограммы отличается от 1/m на величину, не превышающую

			1	1	1
									3		m 1
ˆ			m		m
3 Pi	3			n					m		n		,

то нет оснований утверждать, что равномерность не подтверждается. Другими словами, если оценка входит в интервал:

82

ˆ	1		ˆ
P			3 P
			i
	m				,
то нет основания отвергать гипотезу о равномерности.

Независимость чисел можно проверить, так же как проверяется независимость случайных величин – путем определения ковариации:

			~ ~	~ ~	~	~	. ,
		Kxy cov x, y		M x y	M x	M y
где	~	~	– случайные величины.
	x ,	y

Ковариация может находиться в пределах от – σ[x] ∙ σ[y] до + σ[x] ∙ σ[y], принимая нулевое значение для независимых величин.

Для случайной последовательности подобной характеристикой служит автокорреляционная функция, (или просто корреляционная функция), она отражает корреляцию между элементами последовательности, расположенными на расстоянии s, (s = 0,1,2,...).

Корреляционная функция К(s) идеальной псевдослучайной последовательности должна равняться D[r] при s = 0 и нулю при s > 0, где r – случайная величина, значениями которой являются числа, генерируемые ДСЧ, D[r] – дисперсия равномернораспределѐнной случайной величины в диапазоне (Δ), равная 2/12.

Оценку корреляционной функции можно вычислить по формуле

ˆ

1

n s

1

n s

1

n

ri ri s

ri

ri )

K (s)

(

)(

n

s i 1

n s i 1

n s i s 1 .

Теоретически корреляционная функция равна

0,

s 1,2...

K s

1

s 0.

12

,

где 1/ – значение дисперсии случайной величины с равномерным законом и единичным
12
интервалом.
Действительно:
D[x] 0.5	x2 dx	1
0.5		12 .

Моделирование случайных событий и дискретных случайных величин

Наступление события А с заданной вероятностью Р(А) имитируется с помощью ДСЧ следующим образом (рис.2.1.2).

83

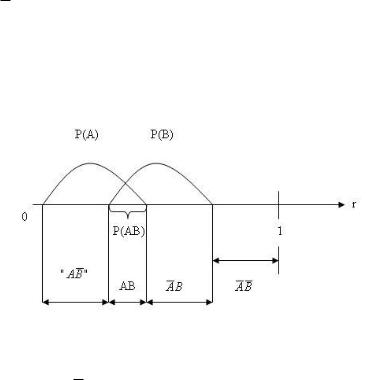
Рис. 2.1.2 Моделирование случайных событий

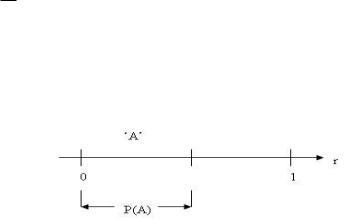
На интервале (0,1) в любой его части (обычно начинают отчет от границ интервала) выделяется область ―A‖ размером P(A). При обращении к ДСЧ выбирается число r и принимается решение о наступлении (или нет) события А:

if r " A" then A if r " A" then A

При моделировании нескольких событий каждому отводится своя область размером, совпадающим с вероятностью события. Если события не совместны, то области не должны пересекаться. При этом одним обращением к ДСЧ определяется выполнение всех событий. При совместных событиях области пересекаются (рис. 2.1.3).

Рис. 2.1.3 Моделирование совместных событий

Например, попадание r в область ‗AB‘ соответствует тому, произошли события и A и B, а попадание r в область " АВ" означает, что наступило только событие A.

Можно также определять наступление событий многократным обращением к ДСЧ. Дискретная случайная величина задается перечнем случайных величин и их

вероятностями, в сумме они равны 1.

То, что случайная величина приняла какое-то значение – есть событие, причем события, связанные с различными значениями несовместны.

Поэтому моделирование распределения дискретной случайной величины аналогично моделированию несовместимых событий и состоит в том, что интервал (0,1) разбивается на области, размеры которых совпадают с вероятностями распределения. На рис. 2.1.4 показано моделирование дискретной случайной величины, принимающей значения 0, 2 и 5 с вероятностями 0,5, 0,2 и 0,3 соответственно.

84

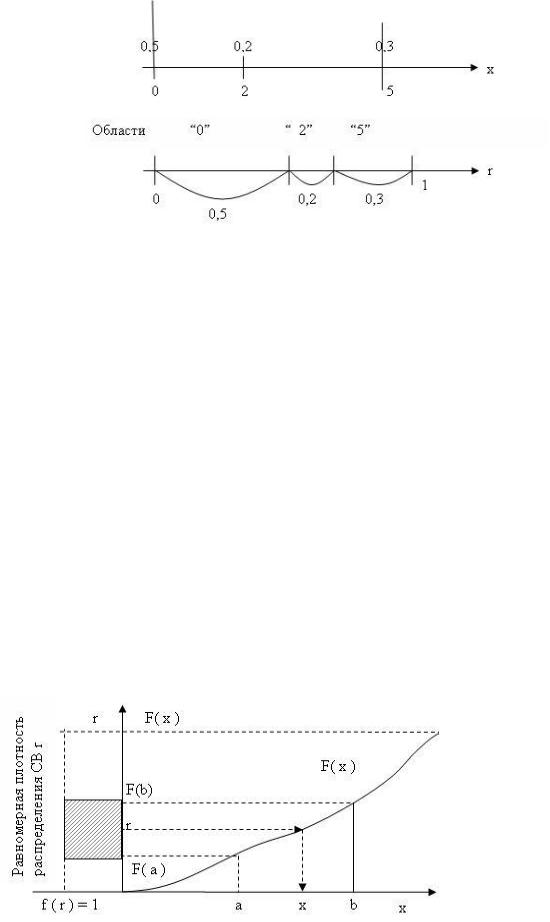
Рис. 2.1.4 Моделирование дискретных величин

Каждый раз при обращении к ДСЧ выбирается то значение случайной величины, в чью область попало случайное число r. Очевидно, что частоты выбора значений будут стремиться к вероятностям.

Лекция 5. Моделирование непрерывных случайных величин с произвольными законами распределения

Данная лекция посвящена моделированию случайных величин с произвольным законом распределения. Сначала подробно раскрывается механизм моделирования случайной величины с произвольным законом распределения, а затем в качестве примера реализации указанного механизма показываются алгоритмы моделирования случайных величин.

Механизм моделирования случайной величины с произвольным законом распределения

Пусть распределение случайной величины X задано плотностью распределения или функцией распределения F(x).

Оказывается, что случайная величина Х будет иметь заданное распределение, если сначала функцию распределения определять как случайную величину с равномерным распределением, а затем Х определять по известному значению функции F(x) (рис.2.2.1).

Рис. 2.2.1 Моделирование СВ с произвольным законом распределения

85

1 e x

F(x) и r имеют одну и туже область значений [0,1] и их можно приравнять. Порядок определения СВ X следующий:

1.Выбирается r (с помощью ДСЧ).

2.Определяется F( x ) = r.

3.Рассчитывается x = F-1 ( r )

Докажем справедливость алгоритма определения Х.

Зададимся некоторым произвольным интервалом (a,b). Известно, что если F (x) – функция распределения СВ X, то

~	b F b F a	(*)
Р a x

Ввиду взаимнооднозначного соответствия между значениями Х и r очевидно, что справедливо равенство

~

Р a x b P F a r F b

F b F a f r F b F a

Таким образом, равенство (*) справедливо и случайная величина X действительно имеет заданное распределение.

Моделирование экспоненциального и нормального распределений

Моделирование экспоненциального распределения

Известно, что функция экспоненциального распределения определяется следующим выражением F (x) 1 e x .

Тогда имеем r .

Получим выражение для определения искомой величины:

x ln 1 r .

Так как СВ (1-r) имеет такое же распределение, что и СВ r, то последовательность случайных чисел, подчиненных экспоненциальному распределению можно определить с помощью следующего соотношения:

x ln(r) .

Таким образом, каждое обращение к ДСЧ позволяет получить СВ с экспоненциальным законом распределения.

Моделирование нормального распределения

Нормальному распределению уделяется особое внимание ввиду его распространенности. В этом случае выразить зависимость x от r в явном виде не всегда возможно и приходиться решать уравнение r = F(x) численно или искать обходные пути.

Существуют несколько эмпирических формул. Например,

86

x			1			3 3
					20n
или
x						41		,
					13440 n2 5		10 3 15
где
	1				n
					ri ,
		n			i 1

где n – число обращений к ДСЧ.

Первая формула дает распределение близкое к нормальному распределению уже при n = 5, а вторая при n = 2.

Обходным можно считать путь, связанный с переходом от одномерного нормального к двумерному. Затем осуществляется переход к полярным координатам. После дополнительных преобразований приходят к аналитической формуле

x 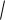2ln(r1 ) sin(2 r2 ) .

Существует еще один путь (и достаточно простой) формирования нормального распределения из равномерного. Он основан на центральной предельной теореме теории вероятностей: сумма случайных величин имеет распределение асимптотически стремящееся к нормальному, если все СВ имеют конечные математические ожидания и дисперсии и ни одна из величин по своему значению резко не отличается от остальных.

Таким образом, СВ с нормальным законом можно получить путем суммирования величин r. Уже при двух слагаемых с равномерным законом получается величина с треугольным законом распределения. Для практических задач можно ограничиться 12-ю слагаемыми. Это позволяет получить распределение с единичной дисперсией.

Для того чтобы распределение нормализовать (нормализованным нормальным называется распределение с нулевым МО и единичным СКО) необходимо от каждой величины r вычесть 0,5:

12	12
x	ri 0,5 ri 6.
i 1	i 1

Следовательно, для получения одного x требуется 12 раз обратиться к ДСЧ.

Приближенные методы моделирования непрерывных случайных величин

Описанный в предыдущем вопросе прием можно делать только для нормального распределения.

Для моделирования СВ с другими законами распределения, не позволяющими выражать в явном виде решения уравнения r = F(x), можно использовать приближенные методы моделирования:

1.Метод численного интегрирования.

2.Интервальный метод.

87

3. Метод просеивания.

Следует отметить, что названия методов условные (т.е. не общепринятые).

Метод численного интегрирования

Для определения x требуется решить уравнение

F(x) = r:

F(x) ax f x dx r .

Последовательность действий:

1.С помощью ДСЧ выбирается r.

2.Интегрируется f(x) до тех пор, пока интеграл не превзойдет r.

3.То значение x, при котором F(x) r и есть искомое значение x.

Для ускорения процесса можно задать опорные точки с известными значениями интеграла и интегрирование выполнять только между ними.

Интервальный метод

Интервальный метод заключается в разбиении области значений х на непересекающиеся интервалы.

Попадание х в эти интервалы есть несовместные события, которые моделируются достаточно просто. При выборе r становится известным, какому интервалу принадлежит х (рис. 2.2.2). Остается перейти от r к х в пределах данного интервала:

x a			ai 1 ai		r
	i
		i 1		i	i
						,

где ai – границы интервалов на оси x; αi – границы интервалов на оси r.

Рис. 2.2.2 Интервальный метод

Поясним рисунок. Ось x разбивается на равные интервалы. Затем на оси r отмечаются точки αi, причем расстояния между ними пропорциональны значениям плотности в соответствующих точках на оси x. Пусть выпало случайное число "3" из интервала α3 – α4. Это соответствует интервалу a3 – a4 на оси x, и по предложенной формуле рассчитывается искомое значение случайной величины x.

Метод просеивания

88

Идея метода состоит в том, что в области задания случайной величины точки выбираются по равномерному закону. Из них принимается равными x только часть, пропорциональная заданной плотности f(x).

Таким образом, плотность генерируемых значений х (плотность точек х) будет пропорциональна функции f(x). Для сортировки точек (относить их к x или нет) требуется еще один генератор, который строится на том же датчике. В итоге для определения значения x требуется как минимум двойное обращение к ДСЧ: при первом выбирается значение x, при втором решается, использовать ли эту точку (рис.2.2.3).

Рис. 2.2.3 Метод просеивания

Алгоритм получения случайных чисел:

1.Выбирается r1 и r2 из датчика случайных чисел.

2.Определяется = a + (b – a) r1 и = M r2.

3.Если f ( ) то принимаем x = , в противном случае возвращаемся снова к расчету .

Лекция 6. Организация компьютерного моделирования инфокоммуникационных систем

В данной лекции раскрываются вопросы реализации моделирования марковских цепей с дискретным и непрерывным временем переходов, а также моделирование систем массового обслуживания с применением ЭВМ.

Введение

Имитация работы конечного автомата сводится к определению реакций автомата на входную последовательность сигналов. При моделировании используются алгоритмические управляющие структуры выбора и множественного выбора, которые достаточно просто программируются на языке высокого уровня.

Если рассматривать методы моделирования динамических систем, в которых входные переменные являются функциями от времени или каких–либо других параметров, то следует учесть, что описываются эти системы дифференциальными и интегральными уравнениями. Например, большая часть законов механики,

89

электротехники, теории упругости, теории управления и т.д. описываются с помощью дифференциальных уравнений.

В связи с этим моделирование динамических систем, связанных с движением тел, с расчетом потоков энергии, с расчетом потоков материальных ресурсов, с расчетом оборотов денежных средств и т.д. в конечном счете, сводится к построению и численному решению дифференциальных уравнений, как правило, II-го порядка (например, методами Эйлера, Рунге-Кутта).

Особый интерес представляют методы имитационного моделирования марковских цепей с дискретным и непрерывным временем переходов и систем массового обслуживания.

Моделирование марковских цепей с дискретным временем переходов

Марковская цепь задается дискретными состояниями, но в отличие от конечных автоматов в них присутствует управление, и переходы из состояния в состояние происходят случайно.

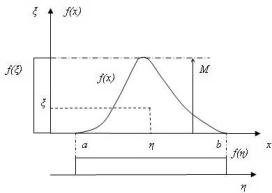
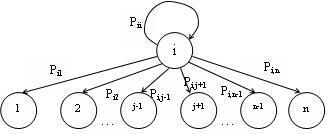
Для марковских цепей переходы осуществляются в соответствии с заданными вероятностями (рис. 2.3.1).

Для моделирования переходов с заданными вероятностями можно воспользоваться принципом моделирования дискретной СВ, описанном в предыдущей лекции: используется ДСЧ, который выдает СВ r, распределенную равномерно в диапазоне от 0 до 1. Далее этот диапазон разбивается на интервалы, равные этим вероятностям.

Рис. 2.3.1 Граф переходов марковской цепи

Переход в новое состояние связывается с попаданием СВ r в интервал: если r попал в интервал ―j", то переход на шаге (t + 1) произойдет в состояние j. В этом случае переходы будут происходить с частотами, в пределе совпадающими с вероятностями.

Моделирование марковских процессов с непрерывным временем переходов

Для марковских процессов с непрерывным временем переходы осуществляются в соответствии с заданными интенсивностями.

Для моделирования можно свести марковский процесс к марковской цепи, разбив время на интервалы t и определив вероятности перехода за это время: Pij ij t . Но,

во-первых, число шагов до перехода могут быть большими (процесс будет медленным), и, во-вторых, могут накапливаться ошибки ввиду конечного значения t . Поэтому

90