
3. Учебно-методическое обеспечение дисциплины(твимс 36л)
.pdf
3. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Конспект лекций (сокращенный)
по теории вероятностей и математической статистике
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Тема 1. Случайные события
Лекция 1
1.Основные понятия и определения теории вероятностей. Классификация событий
2.Классическое определение вероятности. Статистическое определение вероятности. Свойства вероятности событий.
3.Непосредственный подсчет вероятностей. Основные формулы комбинаторики.
Основные понятия и определения теории вероятностей. Классификация событий
Косновным понятиям относятся испытание, исход (событие), вероятность.
Испытанием называют осуществление некоторого комплекса условий, который может быть воспроизведен неограниченное число раз.
Результат испытания называют событием или исходом.
Некоторое событие называется случайным по отношению к определенному комплексу условий, если при его осуществлении оно может произойти, а может и не произойти.
Кнеслучайным относятся достоверные и невозможные события. Достоверное событие обязательно происходит при данном испытании.
Невозможное событие не может произойти ни при одном испытании. События А и В называются несовместными, если при данном
испытании наступление одного из них исключает возможность наступления другого. В противном случае события называются совместными.
События называются единственно возможными, если в результате испытания наступит хотя бы одно из этих событий.
События А1, А2 , ..., Аn образуют полную группу, если они представляют собой совокупность единственно возможных и несовместных событий.
Событие называется противоположным событию А, если оно
заключается в ненаступлении события А. Обозначается А (не А). Взаимно противоположные события всегда образуют полную группу событий, так как они несовместны и единственно возможны.
1

События А1, А2, ..., Аn называются равновозможными, если нет оснований считать, что одно из них наступает чаще других.
Возможность наступления рассмотренных выше событий различна.
Количественную меру возможности наступления события |
называют |
вероятностью этого события. |
|
Рассмотрим действия над событиями. |
|
Суммой или объединением событий А и В называют такое событие С, которое состоит в том, что происходит хотя бы одно из событий А или В. Иногда говорят, что наступит хотя бы А или В.
Объединение событий обозначается одним из следующих способов:
"А+В", "А В", "А или В".
Произведением или пересечением событий А и В называют такое событие С, которое заключается в том, что должно наступить и событие А, и событие В.
Пересечение событий обозначается одним из следующих способов:
"А·В" , "А В", "А и В".
Классическое определение вероятности событий. Свойства вероятности событий
В классической модели вероятность любого события есть отношение числа благоприятствующих событию исходов (М) к общему числу всех равновозможных, единственно возможных и несовместных исходов (N), то есть
P( A ) MN .
Это определение вероятности называют классическим.
Основные свойства вероятности
1.Вероятность достоверного события равна единице.
2.Вероятность невозможного события равна нулю.
3.Вероятность случайного события заключена между 0 и 1, то есть: 0 < P(A) <1.
Тема 2. Основные теоремы теории вероятностей
Лекция 1
1.Теорема сложения вероятностей.
2.Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей.
3.Формула полной вероятности. Формула Байеса.
2

Теорема сложения вероятностей для несовместных событий
Вероятность наступления одного из нескольких несовместных событий равна сумме вероятностей этих событий, то есть
P(A1 или A2 или ...или Аn ) P(A1 ) P(A2 ) ... |
P(An ) . |
Следствие. Сумма вероятностей событий, образующих полную группу событий, равна единице, то есть
P(A1 ) P(A2 ) ... P(An ) 1,
где A1 ,A2 ,...,An – полная группа событий.
Противоположные события A и A образуют полную группу событий, следовательно,
P( A) P( A) 1 .
Теорема сложения вероятностей для совместных событий
Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, то есть
P( A или B) P( A) P( B ) - P(A и B) .
Зависимые и независимые события. Условная вероятность события.
Вероятность события А, вычисленная при условии, что событие В наступило, называется условной вероятностью события А и обозначается -
PB(А)
События называются независимыми, если при данном испытании наступление одного события не изменяет вероятности наступления других, в противном случае события будут зависимыми.
Теорема умножения вероятностей
Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже произошло, то есть
P(A и B) P(A) PA (B) .
Если события A и B независимые, то вероятность их совместного наступления равна произведению их вероятностей, то есть
P(A и B) P(A) P(B).
Теорема умножения вероятностей справедлива для любого конечного числа событий, а именно:
а) для зависимых событий:
3

P( A1 и A2 и A3 и ... и An-1 и An ) P(A1 ) PA1 (A2 ) PA1A2 (A3 ) ... PA1A2 A3 ... An 1 ( An )
б) для независимых событий:
P(A1 и A2 и A3 и ...и An ) P(A1 ) P(A2 ) P(A3 ) ... P(An ).
Формула полной вероятности. Формула Байеса
Вероятность наступления события B с одним из событий A1 , A2 ,..., An ,
образующих полную группу событий, равна сумме произведений вероятностей каждого из событий Ai на соответствующую условную
вероятность события B , то есть
n
P(B) P( A1 ) PA1 (B) P( A2 ) PA2 (B) ... P( An ) PAn (B) P( Ai ) PAi (B).
i 1
Эта формула называется формулой полной вероятности. События Ai (i 1, , n) называют гипотезами.
Предположим, что событие B уже наступило. Требуется определить вероятность того, что событие B наступило при осуществлении, например, гипотезы Ai , то есть найти PB ( Ai ) . Эта вероятность вычисляется по формуле
Байеса (по формуле гипотез):
PB ( Ak ) |
P( Ak ) PA (B) |
||
k |
|
, k = 1,2,…,n. |
|
n |
|
||
|
P( Ai ) PAi |
(B) |
|
|
i 1 |
|
|
Тема 3. Повторные испытания
Лекция 1.
1.Повторные независимые испытания. Формула Бернулли.
2.Асимптотические формулы Пуассона, Муавра-Лапласа.
Повторные независимые испытания. Формула Бернулли.
Испытания называются независимыми относительно события A , если вероятность наступления события A в каждом испытании не зависит от исходов других испытаний. Будем рассматривать испытания, в которых событие A имеет одну и ту же вероятность.
Пусть проводится n независимых испытаний, в каждом из которых событие A может наступить с вероятностью p одинаковой при каждом
испытании, или не наступить (событие A ) с вероятностью q = 1 – p. Тогда вероятность того, что событие A наступит m раз, можно найти по формуле
Бернулли:
Pm ,n (A) C nm pm qn m .
4

Асимптотические формулы Пуассона, Муавра – Лапласа
Если по отношению к событию A проводится большое число испытаний, то вычисление вероятности Pm,n ( A) по формуле Бернулли
становится громоздким. В этом случае для вычисления Pm,n (A) применяются
асимптотические (приближенные) формулы. Одна из таких формул вытекает из теоремы Муавра – Лапласа.
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
e |
u 2 |
|
m |
np |
|
|
|
|
P |
|
(A) |
|
|
|
f (u) , где |
f ( u ) |
|
|
|
2 |
, u |
|
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m ,n |
|
|
npq |
|
|
|
2 |
|
|
|
|
|
|
npq |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Значения функции f (u) |
табулированы. Следует помнить, что функция |
f (u) |
|||||||||||||||||||
четная, то есть |
f ( u) f (u) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если число независимых испытаний n, проводимых по отношению к |
|||||||||||||||||||||
событию A , неограниченно возрастает, а вероятность |
p при каждом |
||||||||||||||||||||
испытании неограниченно |
убывает |
( p 0), |
|
то |
есть |
событие |
A – |
||||||||||||||
маловероятное, при этом m – величина небольшая, то вероятность Pm ,n (A) ,
вычисленная по формуле Муавра – Лапласа, получается с большой погрешностью. В этом случае применяется другая асимптотическая формула, вытекающая из теоремы Пуассона:
P |
(A) |
am |
e a , |
где a np. |
|
|
|
||||
m ,n |
|
m! |
|
|
|
|
|
|
|
||
Обычно эту формулу применяют, когда n 100, a |
np 10. Функция |
||||
Пуассона табулирована при различных значениях a и m .
Тема 4. Случайные величины и способы их описания
Лекция 1.
1.Случайная величина (дискретная и непрерывная). Способы описания случайных величин (табличный, графический, аналитический).
2.Интегральная функция распределения случайной величины, ее свойства.
3.Дифференциальная функция распределения случайной
величины (плотность |
распределения вероятности), ее |
свойства. |
|
4.Выражение интегральной функции через дифференциальную функцию распределения случайной величины.
Лекция 2.
1.Числовые характеристики непрерывной и дискретной случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение.
5
2.Математическое ожидание. Свойства математического ожидания.
3.Дисперсия. Свойства дисперсии.
Случайные величины. Способы их описания
Случайная величина – это переменная величина, которая принимает различные значения в зависимости от случайных обстоятельств с определенными вероятностями для каждого значения. Случайные величины бывают дискретные и непрерывные.
Случайная величина X считается заданной, если известен закон ее распределения, под которым понимают определенное соотношение между
значениями случайной величины xi и соответствующими им вероятностями
pi ( i 1, , n ).
Закон распределения может быть задан:
а) таблично, с указанием всех значений случайной величины и соответствующих им вероятностей, причем сумма всех вероятностей равна единице, то есть
n
pi 1;
i 1
б) аналитически, с помощью интегральной функции (функции распределения вероятностей) F( x ) P( X < x ) и/или дифференциальной функции (плотности распределения вероятностей) f (x) F (x) ;
в) графически, в виде графиков интегральной (для дискретной и непрерывной случайных величин) и/или дифференциальной (для непрерывной случайной величины) функций или в виде полигона (для дискретной случайной величины).
Интегральная функция может быть выражена через дифференциальную:
x
F (x ) f (x )dx .
Вероятность попадания непрерывной случайной величины в интервал ( , ) рассчитывается по одной из следующих формул:
P( X ) F( ) F( ) ;
P( X ) f (x )dx .
6

Числовые характеристики случайной величины
Основными числовыми характеристиками случайной величины X являются математическое ожидание M ( X ) , дисперсия D(X), среднее
квадратическое отклонение (X ) .
Математическое ожидание случайной величины – это среднее
значение случайной величины, взвешенное по вероятностям.
Если случайная величина Х является дискретной и известен ее ряд распределения:
хi |
х1 |
х2 |
х3 |
... |
хn |
|
pi |
р1 |
p2 |
p3 |
... |
pn . , |
|
n
то M ( X ) = хi pi .
i 1
Если случайная величина Х является непрерывной и известна ее дифференциальная функция (плотность распределения вероятностей) f(x).
то M ( X ) = хf ( x )dx .
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть
D(X)= M X M (X ) 2 .
n
D(X) = xi M ( X ) 2 pi – для дискретной случайной величины;
i 1
D(X) = x M (X ) 2 f (x )dx – для непрерывной случайной величины.
Альтернативная формула для вычисления дисперсии
D(X) = M( X 2 ) M 2 ( X ),
то есть дисперсия случайной величины равна математическому ожиданию квадрата случайной величины без квадрата ее математического ожидания.
Средним квадратическим отклонением случайной величины называют арифметическое значение квадратного корня из ее дисперсии, то есть
( X ) 
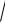 D ( X ) .
D ( X ) .
Дисперсия и среднее квадратическое отклонение характеризуют вариацию (колеблемость) значений случайной величины около ее среднего значения. Так, (X ) показывает, на сколько в среднем отклоняются значения случайной величины от ее математического ожидания.
7
Тема 5. Основные законы распределения случайных величин
Лекция 1.
1.Биномиальный закон распределения случайной величины, его свойства, характеристики случайной величины, полигон распределения.
2.Распределение Пуассона, его характеристики Биномиальное распределение
Лекция 2.
1. Равномерное распределение случайной величины: дифференциальная и интегральная функции распределения, их графики; характеристики распределения; вероятность попадания случайной величины в заданный интервал.
2.Показательное распределение случайной величины: дифференциальная и интегральная функции распределения, их графики, характеристики распределения, вероятность попадания случайной величины в заданный интервал. Характеристическое свойство показательного распределения.
Лекция 3.
1.Нормальный закон распределения случайной величины. Дифференциальная функция распределения. Параметры распределения. Нормированное нормальное распределение. Кривая Гаусса. Влияние параметров распределения на форму и положение нормальной кривой.
2.Интеграл вероятностей (функция Лапласа). Свойства функции Лапласа. Выражение интегральной функции нормального распределения через функцию Лапласа.
3.Вероятность попадания в заданный интервал нормально распределенной случайной величины. Вероятность заданного отклонения значений случайной величины от ее математического ожидания.
4.Распределения Пирсона, Стьюдента, Фишера-Снедекора.
Биномиальный закон распределения случайной величины, его свойства, характеристики случайной величины, полигон распределения
Пусть проводится n независимых испытаний, причем вероятность наступления некоторого события А в каждом испытании постоянна и равна р, то есть P( A) p . При этом событие А может наступить ноль раз (ни разу), или 1, или 2, или ..., или m, ... , или n раз в зависимости от случайных обстоятельств. Следовательно, частота наступления события А есть величина случайная, причем дискретная. Обозначим ее через Х и составим закон
8

распределения вероятности случайной величины Х, который представим в виде следующей таблицы:
|
xi (m) |
0 |
1 |
|
|
|
|
2 |
|
|
|
|
... |
|
|
|
m |
|
|
... |
n-1 |
|
n |
|
|||
|
pi |
q |
n |
npq |
n 1 |
C |
2 |
p |
2 |
q |
n 2 |
|
... |
C |
m |
p |
m |
q |
n m |
... |
np |
n 1 |
q |
p |
n |
||
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|||||||||||||
|
Каждое значение случайной величины рассмотрено как событие. |
||||||||||||||||||||||||||
Соответствующие вероятности pi найдены по формуле Бернулли: |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
P |
|
A |
Cm pmqn m . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
m,n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Составленный закон распределения называется биномиальным законом |
||||||||||||||||||||||||||
распределения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Нетрудно убедиться, что pi Cnm pm qn m |
( p q)n 1n 1. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Биномиальное распределение обладает следующими свойствами: с |
||||||||||||||||||||||||||
возрастанием частоты m от 0 до n вероятности |
Pm,n A |
сначала растут до |
|||||||||||||||||||||||||
некоторого момента, а потом начинают убывать. Это распределение асимметрично, кроме случая, когда р=0,5.
Частота наступления события A , которой соответствует наибольшая вероятность Pm,n ( A) , называется наивероятнейшей частотой и обозначается
m0, то есть Pm0 ,n A Pm0 1,n А и Pm0 ,n A Pm0 1,n А .
Найдем m0 из этих двух неравенств, используя формулу Бернулли: np q m0 np p .
При достаточно большом n наивероятнейшая частота становится близка к np , то есть m0 [np] .
Числовые характеристики случайной величины Х (частоты m наступления события A в n независимых испытаниях):
М Х М m np;
D( X ) D m npq ;
( X ) (m) 
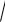 npq .
npq .
Равномерное распределение
Непрерывная случайная величина X имеет равномерное распределение, если плотность распределения вероятности постоянна в интервале ( a, b), а вне его равна нулю, то есть
9
0
f ( x ) 1
b a
0
,если
,если
,если
x a ,
a x b ,
x b .
Интегральная функцию равномерного распределения:
|
0 |
, если |
x a , |
|
|
|
|
x - a |
|
|
|
F( x ) |
|
, если |
a x b , |
|
|||
b a |
|
x b . |
|
|
1 |
, если |
|
|
|
|
|
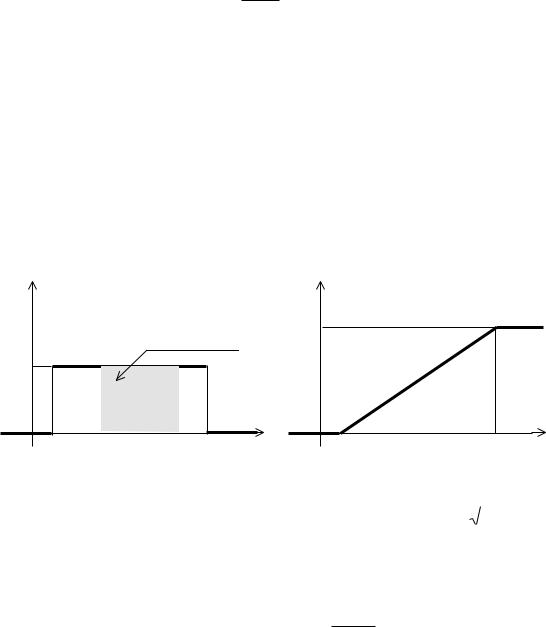
Графики функций f (x ) и F( x ) имеют вид:
f(x) |
|
|
|
|
|
F(x) |
|
|
|
|
|
|
P |
X ) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
b-a |
|
|
|
|
|
|
|
|
|
0 |
a |
|
|
b |
x |
0 |
a |
b |
x |
Характеристики равномерного распределения:
|
|
|
(b a)2 |
|
|
|
|
|
a b |
|
(b a) 3 |
|
|||
M ( X ) |
|
; D( X ) = |
|
; ( X ) |
|
|
. |
2 |
12 |
6 |
|
||||
|
|
|
|
|
|||
Вероятность попадания равномерно распределенной случайной величины в интервал ( , ) ( a, b) находится по формуле:
P( < X < ) = . b a
Показательное распределение
Непрерывная случайная величина X имеет показательное
распределение, если ее плотность распределения вероятности имеет вид:
0 |
, ecли |
x 0, |
f (x ) |
x , ecли |
x 0, |
e |
||
|
|
|
где 0 – параметр распределения.
Интегральная функция показательного распределения имеет вид:
10
