3. Учебно-методическое обеспечение дисциплины(твимс 36л)

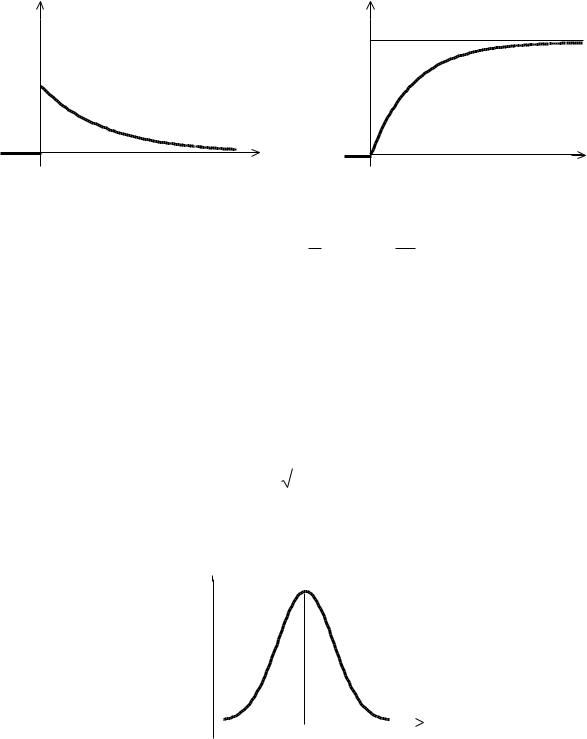
	0	, ecли	x 0,
F( x ) 1 e x , ecли			x 0.

Графики дифференциальной и интегральной функций, соответственно, имеют вид:

f(x)		F(x)
		1
0	x	0	x

Характеристики показательного распределения:

M ( X ) ( X ) 1 , D( X ) 12 .

Вероятность попадания случайной величины в интервал ( , ) (0, ) рассчитывается по формуле: P( < X < ) e e .

Нормальное распределение

Непрерывная случайная величина X имеет нормальное распределение, если ее плотность распределения вероятности имеет вид:

		1					(x a)2
f (x)					e		2 2
			2

где a и – параметры распределения, причем a График дифференциальной функции

нормальной кривой, или кривой Гаусса:

,

= M(X), = (X).

распределения называют

f(x)

0	a	x

11

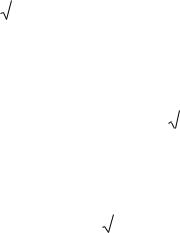
Если M (X) = 0,

(X) = 1, то нормально распределенная случайная

величина называется

нормированной, ее

дифференциальная функция

1

x 2

распределения f (x)

e

2 табулирована.

2

Вероятность попадания нормально распределенной случайной

величины в интервал ( , ) находим по формуле:

1

(x a)2

P( X ) f (x)dx

e

2 2

dx.

2

Данный интеграл выражается через функцию Лапласа, которую еще называют интегралом вероятностей и обозначают Ф(t):

			1		t		x2
	Ф(t)				e		2	dx .
			2
				0

Функция Лапласа – это вероятность попадания нормированной нормально распределенной случайной величины в интервал ( 0, t).

Таким образом, вероятность попадания значений нормально распределенной случайной величины в интервал ( , ):

		a			a
	P( X ) Ф			Ф		.

При решении задач часто возникает необходимость определения вероятности отклонения нормально распределенной случайной величины от ее математического ожидания:

P	X a		2Ф		.

Распределения, связанные с нормальным распределением (распределения Пирсона, Стьюдента, Фишера - Снедекора)

Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения. Однако на практике встречаются и другие законы, связанные с нормальным. Они представляют собой распределения некоторых функций от нормально распределенной величины. Рассмотрим такие распределения.

	Распределение Пирсона (распределение 2 )
Пусть Х1 , Х 2 ,...,Х k -		независимые случайные величины,		имеющие
		распределение, М Х i 0 , Х i 1,
нормированное	нормальное				i 1, k .
Величина 2 ,	равная сумме квадратов случайных величин Х		i	,	то есть
					12

2	k
	X 2	, также будет случайной величиной. Она имеет распределение
	i
	i 1
Пирсона или распределение 2			(хи-квадрат) с k степенями свободы.
	Из определения следует,		что случайная величина 2 может принимать

только неотрицательные значения. Число степеней свободы k распределения 2 является параметром этого распределения, поэтому часто распределение Пирсона с k степенями свободы обозначают 2 k .

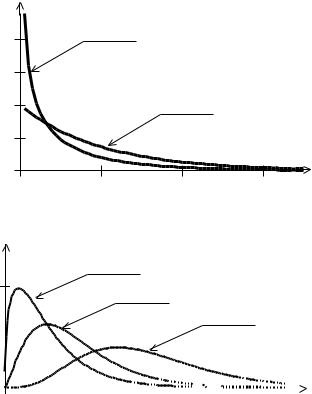
Графики функции	плотности вероятности распределения			2 с
различными степенями	свободы изображены ниже, где	2	Х 2	k 1 ;
		1	1

2	Х 2	Х 2	k 2 ; 2	Х 2	Х 2	Х 2	k 3 .
2	1	2	3	1	2	3
			f( )		k= 1
			1
			0,75
			0,5				k= 2
			0,25
			0
			0		2		4	6
			f( )		k= 3

0,25

k= 5

k= 10

0
																									20
0		10
Можно показать, что числовые характеристики 2 -распределения с k
степенями свободы равны: M ( 2 ) k и D( 2 ) 2k .
С увеличением числа		степеней свободы																				k распределение 2

приближается к нормальному. Это распределение асимметричное (имеет положительную правостороннюю асимметрию).

Распределение Стьюдента (t-распределение)

Пусть Z - нормированная нормально распределенная случайная

величина, то есть М Z 0,	Z 1, а	2 - случайная величина, не
		13

зависящая от Z и имеющая распределение 2 с k степенями свободы. Тогда

случайная величина t	Z	имеет распределение Стьюдента (t-

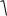1k 2 k

распределение) с k степенями свободы.

Из данного определения следует, что случайная величина t может принимать значения любого знака, а число степеней свободы k является параметром этого распределения.

Числовые характеристики распределения Стьюдента: М t 0 ,

D t k . k 2

Кривая распределения Стьюдента симметрична относительно оси ординат, как и кривая нормированного нормального распределения, но является более пологой по сравнению с нормированной нормальной кривой.

				f(t)
						k =10
				0,4
				0,3		k =1
				0,2
				0,1
				0				t
	-3	-2	-1	0	1	2	3

С ростом числа степеней свободы k распределение Стьюдента быстро приближается к нормированному нормальному распределению. Практически при k>30 можно считать t-распределение приближенно нормальным.

Распределение Фишера - Снедекора (F-распределение)

Пусть

2 (k )

и

2 (k

2

)

- независимые случайные величины, имеющие

1

распределение

2

с

k

и k

2

степенями свободы, соответственно. Тогда

1

случайная величина

F

2 (k

1

) / k

1

имеет распределение

Фишера -

2 (k

2

) / k

2

Снедекора (F-распределение) с k1

и k2 степенями свободы.

Из определения следует, что случайная величина F может принимать

только положительные

значения. Степени свободы k1 и k2

являются

14

параметрами этого распределения, поэтому часто распределение Фишера -
Снедекора обозначают F k1 , k2 .
График функции плотности вероятности F-распределения показан
ниже при различных k1	и k2 .	Распределение асимметричное,			удлиненное
вправо.
f(F)	k 1=1, k 2=5
1		k 1=10, k 2=10
0,75
0,5
0,25
0
0	1	2	3	4F

Числовые характеристики распределения Фишера - Снедекора:

k

2

2k 2 k k

2

2

2

1

М F

, D F

, k2>4 .

k2 2

k k

2

2 2

k

2

4

1

При k

lim М F 1

, а

lim D F

2

.

2

k2

k2

k1

При больших

значениях

k1

и k2

F-распределение приближается к

нормальному.

Тема 6. Закон больших чисел. Центральная предельная теорема

Лекция 1.

1.Неравенство Маркова. Неравенство Чебышева. Теорема Чебышева, частный случай теоремы. Теорема Бернулли.

2.Особая роль нормального закона распределения: центральная предельная теорема

Кзакону больших чисел относят, в основном, следующие теоремы: лемма Маркова (неравенство Маркова), неравенство Чебышева, теоремы Чебышева, Бернулли, Пуассона.

Закон больших чисел - это обобщенное название указанных предельных теорем, из которых следует, что при неограниченном увеличении числа испытаний при соблюдении определенных условий средние величины стремятся к некоторым постоянным значениям.

15

Неравенство Маркова

Если случайная величина Х принимает только неотрицательные значения и имеет конечное математическое ожидание, то для некоторого положительного числа

P( X ) 1 M ( X ) .

Данное неравенство называют неравенством Маркова.

Неравенство Чебышева

Вероятность того, что отклонение случайной величины Х от ее математического ожидания M ( X ) по абсолютной величине не превзойдет

некоторого положительного числа , будет больше разности 1

D( X )

,

то

2

есть

P(| X M ( X ) | ) 1

D( X )

.

2

Другая форма неравенства Чебышева:

P

Х М Х

D Х

.

2

Теорема Чебышева

Если Х1, Х 2 ,..., Х n

- независимые

случайные

величины,

имеющие

вполне определенные

математические

ожидания

М ( Xi ) ai , i 1, n ,

а

дисперсии их равномерно ограничены, то есть D Х i C , где С - постоянное

число, то при неограниченном увеличении числа случайных величин с вероятностью, близкой к единице, можно утверждать, что отклонение

средней арифметической случайных величин Х от средней арифметической

их математических ожиданий M ( X )

по абсолютной величине будет сколь

угодно малым, то есть

lim Р

1.

Х

М Х

n

Х1, Х 2 ,...,Х n - независимые

Частный случай теоремы Чебышева: если

случайные величины, имеющие

равные

математические ожидания

М X i a ( i

), дисперсии

1, n

которых равномерно ограниченны, то при

неограниченном увеличении

числа

случайных величин с вероятностью,

16

lim Р Х а 1.

n

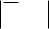
близкой к единице, можно утверждать, что средняя арифметическая этих случайных величин отклоняется от их математического ожидания по абсолютной величине не более, чем на сколь угодно малую положительную величину, то есть

Теорема Бернулли

Если в каждом из n независимых испытаний вероятность р наступления события А постоянна, то при неограниченном увеличении числа испытаний с вероятностью, близкой к единице, можно утверждать, что частость наступления события отклоняется от вероятности р по абсолютной величине не более, чем на сколь угодно малую положительную величину, то есть

				m
	lim P					p			1 .
					n
	n

Центральная предельная теорема (теорема Ляпунова)

Рассмотренные выше теоремы являются одной из форм закона больших чисел. Эти теоремы утверждают о приближении некоторых случайных величин к определенным предельным значениям независимо от их распределения. В теории вероятностей существует другая группа теорем, относящихся к предельным законам распределения суммы случайных величин. Эта группа теорем носит общее название центральной предельной теоремы. Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на сумму составляющих случайных величин. Так, если независимые случайные величины не распределены по нормальному закону, то можно наложить на них некоторые ограничения и их сумма будет иметь нормальное распределение.

Теорема Ляпунова

Распределение суммы независимых случайных величин Хi i 1,2,...,n

приближается к нормальному распределению при неограниченном увеличении числа случайных величин, если выполняются следующие условия:

1)все величины имеют конечные математические ожидания и дисперсии;

2)ни одна из величин по своему значению резко не отличается от всех остальных.

Примечание. Фактически приведена не теорема Ляпунова, а одно из ее следствий, которого достаточно для практического применения.

Частный случай теоремы Ляпунова

17

	Если случайные величины	Х1 , Х 2 ,..., Х n независимые, имеют равные
	математические ожидания	М X		a , i			и равные	дисперсии
			i		1, n
	D Х i 2 , то не только случайная величина						n			1	n
						Х Х i , но и		Х			Х i
							i 1			n i 1

имеют распределение, близкое к нормальному.

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Выборочный метод

Лекция 1

1.Генеральная совокупность и выборка. Ряды распределения (дискретные и интервальные).

2.Графическое изображение рядов распределения.

Лекция 2

1.Выборочные характеристики статистических распределений: средняя, мода, медиана, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Генеральная совокупность и выборка. Ряды распределения.

Полученная в результате статистического наблюдения выборка из n значений (вариант) изучаемого количественного признака X образует

вариационный ряд. Ранжированный вариационный ряд получают,

расположив варианты xj , где j 1,2, , n , в порядке возрастания значений, то есть x1 x2 x j xn .

Изучаемый признак X может быть дискретным, то есть его значения отличаются на конечную, заранее известную величину (год рождения, тарифный разряд, число людей), или непрерывным, то есть его значения отличаются на сколь угодно малую величину (время, вес, объем, стоимость).

Частотой mi в случае дискретного признака X называют число одинаковых вариант xi , содержащихся в выборке. В ранжированном вариационном ряду одинаковые варианты очевидно расположены подряд.

Вариационный ряд для дискретного признака X принято наглядно и компактно представлять в виде таблицы, в первой строке которой указаны k различных значений xi изучаемого признака, а во второй строке – соответствующие этим значениям частоты mi , где i 1,2, , k . Такую таблицу называют статистическим (выборочным) распределением.

Статистическое распределение для непрерывного признака X принято представлять интервальным рядом – таблицей, в первой строке которой указаны k интервалов значений изучаемого признака X вида (xi–1 – xi ), а во

18

второй строке – соответствующие	этим интервалам частоты mi ,		где
i 1,2, , k .Обозначение (xi–1 – xi ) – указывает не разности,		а все значения
признака X от xi–1 до xi , кроме правой границы интервала xi .
Для непрерывного признака X	частота mi – число	различных	xj ,

попавших в соответствующий интервал: xj [xi–1 ; xi ).

Если число различных значений дискретного признака очень велико, то для удобства дальнейших вычислений и наглядности статистическое распределение такого дискретного признака также может быть представлено в виде интервального ряда.

Вместо частот mi во второй строке могут быть указаны относительные

	частоты	wi	mi	(частости). Очевидно,			что сумма частот равна объему
			n
	выборки	(выборочной совокупности) n				,	а	сумма относительных частот
	(частостей) равна единице:
				k	k		k	m
				mi n,	wi			i	1.
				i 1	i 1		i 1	n

Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд распределения называют кумулятивным.

Накопленной частотой называется число значений признака Х, меньших заданного значения x: H(x) = m(Х x), то есть, число вариант xj в выборке, отвечающих условию xj < x.

Накопленной относительной частотой (накопленной частостью)

называется отношение числа значений признака Х, меньших заданного

	значения x , к объему выборки n : F x	H (x)		m( X x)	, то есть, доля
		n		n

вариант xj в выборке, отвечающих условию xj < x.

По аналогии с теоретической функцией распределения генеральной совокупности F (x ) , которая определяет вероятность события Х x :

F (x ) = P(Х x ), вводят понятие эмпирической функции распределения

F * (x ) , которая определяет относительную частоту этого же события Х x ,

	то есть F * (x ) =	m( X x)	. Таким образом, эмпирическая функция
		n

распределения F * (x ) задается рядом накопленных относительных частот.

Графическое изображение статистических распределений

Для наглядности принято использовать следующие формы

графического представления статистических распределений:

дискретный ряд изображают в виде полигона. Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами ( x i

19

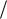
, m i); аналогично, полигон относительных частот – ломаная, отрезки которой соединяют точки с координатами ( xi , wi );

интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых – интервалы длиной hi , а высоты – плотности частот

mi

. В

случае

гистограммы

относительных

частот

высоты

hi

прямоугольников – плотности относительных частот

wi

mi

. Здесь в

n h

h

i

i

общем случае hi

xi xi 1 , однако на практике чаще всего полагают

величину

h

одинаковой

для

всех

интервалов:

hi h (xk x0 )

k ,

где i 1,2, k .

Очевидно

для

ранжированного

вариационного ряда

x0 xmin x 1 ;

xk xmax x n .

В скобках указаны

индексы j исходного ранжированного вариационного ряда.

кумулятивные ряды графически изображают в виде кумуляты. Для ее

построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат – накопленные частоты Н( x ) или относительные накопленные частоты F * (x ) , а затем точки с координатами ( x i ; H( x i )) или ( x i ; F * (x i ) ) соединяют отрезками прямых.

Выборочные характеристики статистических распределений

1) средние

Выборочная

а) характеризует типичное для выборки значение

средняя:

признака X;

б) приближенно характеризует (оценивает) типичное

для генеральной совокупности значение признака X

(см. п. 3.2);

1

n

– средняя арифметическая;

x

в

x j

применяется к вариационному ряду

n j 1

(данные наблюдения не

сгруппированы);

k

– взвешенная средняя

xi mi

1

k

k

арифметическая (частоты mi , и

в

i 1

xi mi

в xi wi

x

x

частости wi называют весами);

k

mi

n i 1

i 1

используется, если данные

i 1

сгруппированы; непосредственно

применима только к статистическому

распределению дискретного

признака (дискретному ряду).

20