3. Учебно-методическое обеспечение дисциплины(твимс 36л)

Структурные (порядковые) средние.

Если

x

в = хмo = хме , то

распределение симметричное.

При нарушении симметрии

равенство нарушается (хотя бы

одно).

xме

x

j

x

j

1

, если n = 2j – четное;

Медиана – середина

ранжированного вариационного

2

ряда; согласно

хме = хj+1 , если n = 2j+1 – нечетное.

определению имеем:

F x

1

.

ме

2

хмo = xi , если mi = mmax (справедливо только

Мода – наиболее часто

для дискретного ряда).

встречающееся значение

признака X.

2) характеристики вариации (рассеяния)

– выборочная дисперсия есть выборочная средняя

D

(x x )2

арифметическая квадратов отклонений значений признака

в

в

Dв

x

2

2

X от выборочной средней

x

в (равна “среднему квадрату

xв

без квадрата средней”):

1

n

– выборочная дисперсия;

Dв

(x j

x

в )2

применяется к вариационному ряду

n j 1

(данные наблюдения не

сгруппированы);

k

– выборочная взвешенная дисперсия;

(xi

в )2 mi

x

k

используется, если данные

1

Dв

i 1

(xi

x

в )2 mi

сгруппированы; непосредственно

k

n i 1

применима только к

mi

i 1

статистическому распределению

k

Dв

(xi

в )2 wi

дискретного признака (дискретному

x

i 1

ряду);

1

n

– средний квадрат есть выборочная

x2

x

2j

средняя арифметическая квадратов

n j 1

значений признака X (для

1

k

x2

xi2 mi

вариационного ряда и для

n i 1

дискретного распределения

соответственно).

– выборочное среднее квадратическое отклонение есть

σв

Dв

арифметическое значение корня квадратного из дисперсии;

оно показывает, на сколько в среднем отклоняются значения xj

признака X от выборочной средней

x

в .

21

R = хmax – хmin					– размах вариации.
v σв 100 %					– коэффициент вариации; применяют для сравнения
					вариации признаков сильно отличающихся по величине,
	xв
					или имеющих разные единицы измерения (разные
					наименования).

Замечание. Если исходный вариационный ряд недоступен, приведенные выше формулы вычисления выборочных характеристик, применимые только к дискретному ряду, могут быть использованы для приближенного вычисления выборочных характеристик непрерывного признака, представленного интервальным рядом. Для этого предварительно каждый интервал xi–1–xi заменяется его серединой xi = (xi–1+ xi) / 2, то есть

производится замена интервального ряда дискретным, соответствующим ему приближенно.

Тема 8. Статистическое оценивание

Лекция 1

1.Понятие статистических оценок параметров распределения.

2.Точечные оценки. Свойства статистических оценок параметров распределения (несмещенность, состоятельность, эффективность).

Лекция 2

1.Интервальные оценки. Точность оценки. Доверительная вероятность (надежность оценки).

2.Доверительные интервалы для оценки математического ожидания нормально распределенной случайной величины при известном и неизвестном среднем квадратическом отклонении.

Точечные оценки параметров распределения

Задачу статистического оценивания, а также основные виды статистических оценок, рассмотрим для частного случая: пусть признак X генеральной совокупности распределен нормально, то есть теоретическое распределение имеет вид:

		1					( x a)2
f (x)					e		2 2
			2

с параметрами: a M (X ) xген – математическое ожидание признака X ;

M ((X M ( X ))2 ) ген – среднеквадратическое отклонение признака

X.

22

Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах.

Точечной оценкой генеральной средней xген и параметра a может служить выборочная средняя xв .

Точечными оценками генеральной дисперсии Dген 2 могут служить

выборочная дисперсия Dв , или,

при малых объемах выборки n ,

исправленная выборочная дисперсия:

S 2

n

D .

n 1

в

Точечными оценками для генерального среднеквадратического

ген

σв

отклонения

могут

служить:

Dв

– выборочное среднее

квадратическое

отклонение

или

S

S 2

– исправленное

выборочное

среднее квадратическое отклонение.

Для

того

чтобы

точечные

статистические

оценки

обеспечивали

“хорошие” приближения неизвестных параметров, они должны быть

несмещенными, состоятельными и эффективными.

Пусть – точечная оценка неизвестного параметра .

Несмещенной называют такую точечную статистическую оценку ,

математическое ожидание которой равно оцениваемому параметру:

M .

Состоятельной называют такую точечную статистическую оценку,

которая при n стремится по вероятности к оцениваемому параметру.

В частности, если дисперсия несмещенной оценки при n стремится к нулю, то такая оценка оказывается и состоятельной.

Эффективной называют такую точечную статистическую оценку,

которая при фиксированном n имеет наименьшую дисперсию.

Можно показать,

что выборочная средняя

x

в является несмещенной,

состоятельной и эффективной оценкой генеральной средней

x

ген .

Интервальные оценки параметров распределения

Для построения интервальной оценки рассмотрим событие,

заключающееся в том,

что отклонение точечной оценки параметра

от

истинного значения этого параметра

по абсолютной величине

не

превышает

некоторую

положительную величину . Вероятность такого

события

P

. Заменив

неравенство

на

равносильное, получим:

23

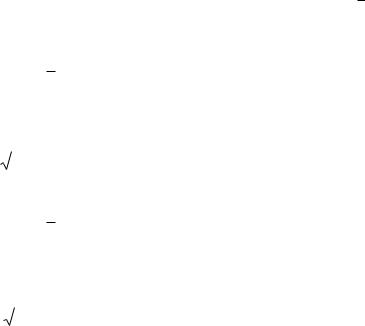
P				.
Вероятность того, что		доверительный интервал ( , )

заключает в себе (покрывает) неизвестный параметр равна и называется

доверительной вероятностью или надежностью интервальной оценки.

Величину называют точностью оценки.

Построим интервальную оценку параметра a xген для двух случаев:

1) параметр нормального закона распределения признака Х генеральной совокупности известен. В этом случае интервальная оценка параметра a xген с заданной надежностью определяется формулой:

							в a		в ,
						x		x
где =	t			,	t – аргумент функции Лапласа: Ф(t) =					.
		n								2

2) параметр нормального закона распределения признака Х генеральной совокупности неизвестен. В этом случае интервальная оценка параметра a xген с заданной надежностью определяется формулой:

						в a		в ,
					x		x
где =	t	S		, S – точечная оценка параметра , t						t( , n) – значения
		n

распределения Стьюдента, которые находим по таблице.

Тема 9. Проверка гипотез

Лекция 1

1.Статистические гипотезы. Ошибки 1-го и 2-го рода. Уровень значимости.

2.Статистический критерий. Наблюдаемое значение критерия. Критическая область. Область принятия гипотезы. Критические точки. Отыскание критической области.

Лекция 2

1.Проверка гипотезы о нормальном законе распределения признака генеральной совокупности.

2.Проверка гипотезы о равенстве дисперсий двух нормально распределенных генеральных совокупностей.

Лекция 3

1.Сравнение средних двух нормально распределенных генеральных совокупностей при неизвестных дисперсиях.

24

2.Сравнение средних двух нормально распределенных генеральных совокупностей при известных дисперсиях.

3.Проверка гипотезы о равенстве вероятностей.

Статистические гипотезы. Ошибки первого и второго рода

Под статистической гипотезой понимают всякое высказывание о генеральной совокупности, которое можно проверить статистически, то есть опираясь на результаты наблюдений в случайной выборке. Рассматривают два вида статистических гипотез: гипотезы о законах распределения генеральной совокупности и гипотезы о параметрах известных распределений.

Подлежащая проверке гипотеза называется нулевой, или основной, и обозначается Н0. Нулевой гипотезе противопоставляют конкурирующую, или альтернативную, гипотезу, которую обозначают Н1.

При проверке статистической гипотезы пользуются специально составленной случайной величиной, называемой статистическим критерием (или статистикой).

При проверке гипотезы возможны ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута нулевая гипотеза, хотя на самом деле она верна.

Ошибка второго рода состоит в том, что будет принята нулевая гипотеза, хотя в действительности верна конкурирующая.

Вероятность совершить ошибку первого рода называют уровнем значимости критерия и обозначают .

В большинстве случаев уровень значимости критерия принимают равным 0,01 или 0,05.

Вероятность совершить ошибку второго рода обозначают .

Вероятность 1 не совершить ошибку второго рода, то есть отвергнуть

нулевую гипотезу, когда она неверна, называется мощностью критерия.

Единственный путь одновременного уменьшения риска ошибок заключается в увеличении объема выборки.

Статистический критерий. Критическая область. Область принятия гипотезы. Отыскание критической области

Статистическую гипотезу проверяют с помощью специально подобранной случайной величины, точное или приближенное распределение которой известно (обозначим ее К). Эту случайную величину называют

статистическим критерием (или просто критерием).

25

Kнабл

Множество значений критерия, при которых нулевая гипотеза отвергается, называется критической областью. Будем обозначать критическую область через W.

Множество значений критерия, при которых нулевая гипотеза принимается, называется областью принятия гипотезы (или областью

допустимых значений критерия). Будем обозначать эту область как W .

Для проверки справедливости нулевой гипотезы по данным выборок вычисляют наблюдаемое значение критерия. Будем обозначать его Кнабл.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия попало в критическую область (то есть Kнабл W ), то нулевую гипотезу отвергают; если

же наблюдаемое значение критерия попало в область принятия гипотезы (то естьW ), то нет оснований отвергать нулевую гипотезу.

В зависимости от вида конкурирующей гипотезы Н1 строят

одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области. Точки, отделяющие критическую область W от области принятия гипотезы W , называют критическими точками и обозначают kкрит. Для отыскания критической области необходимо знать критические точки.

Правосторонняя критическая область может быть описана неравенством W :К>kкрит. пр, где предполагается, что правая критическая

точка kкрит. пр>0. Для нахождения kкрит. пр задают сначала уровень значимости

критерия . Далее правую критическую точку kкрит. пр находят из условия
PH0 K kкрит.пр .
Левосторонняя критическая область описывается неравенством W :
К<kкрит. л, где	kкрит.л<0.	Критическую точку kкрит.л	находят	из условия
PH 0 (К<kкрит. л)	, то	есть вероятность того, что	критерий	принимает

значение, меньшее kкрит.л, равна принятому уровню значимости , если нулевая гипотеза верна.

Двусторонняя критическая область W описывается следующими

неравенствами: (К<kкрит.л или К>kкрит. пр), где предполагается, что kкрит.л<0 и kкрит. пр>0. Такая область представляет собой множество достаточно больших

по модулю значений критерия. Критические точки находят из требования:

PH 0 (К<kкрит. л)+ PH 0 (К>kкрит. пр)= .

Если распределение критерия К симметрично относительно начала координат, то критические точки будут располагаться симметрично относительно нуля, поэтому kкрит. л = - kкрит. пр. Тогда двусторонняя критическая область становится симметричной и может быть описана

следующим неравенством: К >kкрит. дв, где kкрит. дв = kкрит. пр Критическую точку kкрит. дв можно найти из условия

Р(К<-kкрит. дв)=Р(К>kкрит. дв)= 2 .

26

Проверка гипотезы о нормальном распределении генеральной совокупности

Во многих практических задачах точный закон распределения исследуемого признака Х генеральной совокупности неизвестен. В этом случае необходимо проверить гипотезу о предполагаемом законе распределения. Выдвигаются нулевая гипотеза Н0 и ей конкурирующая Н1.

Н0: признак Х имеет нормальный закон распределения.

Н1: признак Х имеет закон распределения, отличный от нормального. Нулевая гипотеза проверяется с помощью критерия согласия. Критерий 2 (“хи-квадрат”) Пирсона – наиболее часто употребляемый

критерий, может применяться для проверки гипотезы о любом законе распределения. Независимо от того, какое распределение имеет Х, распределение случайной величины 2:

	s	(mэ mт )2
2			i i	,
			mт
	i 1
			i
где m э – эмпирические частоты,	m т		– теоретические частоты; при		n
i		i

стремится к 2 – распределению с k степенями свободы.

Теоретические частоты определяются, исходя из предположения о законе распределения генеральной совокупности, в данном случае о

нормальном законе. Так как

p

mi

, где рi – теоретическая вероятность, то

i

n

m т

n p .

i

i

Для дискретного ряда:

u2

h

f (u

xi xв

f (u)

1

e

p

) , где

u

,

2 –дифференциальная

i

в

i

i

в

2

функция нормированного нормального распределения, шаг h xi xi 1 , xв – выборочная средняя, σв – выборочное среднее квадратическое отклонение.

Для интервального ряда:

	x
			i		x	в
pi P(xi 1
	X xi ) Ф			в

	x
			i 1		x	в
	Ф		в

, где Ф(t) – функция

Лапласа.

Рассчитав теоретические частоты, находят набл2 . Из таблицы

критических точек распределения 2 по заданному уровню значимости

(достаточно малая вероятность) и числу степеней свободы k находят крит2 ( ,

k) – границу правосторонней критической области. Здесь k = s – r – 1 , где s – число различных значений xi дискретного или число интервалов (xi–1 – xi ) непрерывного признака Х, r – число параметров предполагаемого закона

27

распределения, для нормального распределения r = 2, отсюда k = s – 3. Затем сравнивают набл2 и крит2 ( , k) и делают вывод.

При формулировке вывода руководствуются следующим

правилом:

если наблюдаемое значение критерия набл2 попало в область принятия гипотезы ( набл2 крит2 ( , k)), то нет оснований отвергать нулевую гипотезу, по данным наблюдения признак Х имеет нормальный закон распределения, расхождение между эмпирическими и теоретическими частотами ( miэ и miт ) случайное;

если наблюдаемое значение критерия набл2 попало в критическую

область ( 2	2	( , k)), то нулевая гипотеза отвергается,
набл	крит

справедлива конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, расхождение между

эмпирическими и теоретическими частотами ( miэ и miт ) значимо.

Проверка гипотезы о равенстве дисперсий двух нормально распределенных генеральных совокупностей (выборки независимые)

Даны две генеральные совокупности Х и Y, которые имеют нормальный закон распределения. Есть основание предположить, что их генеральные дисперсии равны. Чтобы проверить справедливость этого предположения, выдвигаем основную и конкурирующие гипотезы.

Н0: D(Х) = D(Y),

Н1: D(Х) D(Y) (критическая область правосторонняя).

Для проверки нулевой гипотезы делают выборки из данных генеральных совокупностей объемами, соответственно, nx и ny, по данным выборок рассчитывают несмещенные точечные оценки генеральных

дисперсий S 2	,	S 2	. Затем с помощью случайной величины	F	Sбольшая2	,
x		y			Sменьшая2
которая имеет распределение Фишера – Снедекора с k1 n1 1				и k2 n2 1

степенями свободы, проверяется нулевая гипотеза. Здесь: n1 – объем

выборки, по которой рассчитана Sбольшая2 , n2 – соответственно, S меньшая2 .

По выборочным данным рассчитывают Fнабл, по таблице критических точек распределения Фишера – Снедекора находят Fкрит( , k1, k2) – границу правосторонней критической области, а затем сравнивают Fнабл и Fкрит( , k1, k2) и делают вывод.

При формулировке вывода руководствуются следующим правилом:

28

если наблюдаемое значение критерия Fнабл попало в область принятия гипотезы (Fнабл Fкрит( , k1, k2)), то нет оснований отвергать нулевую гипотезу, по данным наблюдения D(Х) = D(Y), расхождение между исправленными выборочными дисперсиями случайное;

если наблюдаемое значение критерия Fнабл попало в критическую область (Fнабл Fкрит( , k1, k2)), то нулевая гипотеза отвергается,

справедлива конкурирующая гипотеза: D(Х) D(Y), расхождение между исправленными выборочными дисперсиями значимо.

Сравнение средних двух нормально распределенных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)

Даны две генеральные совокупности Х и Y, имеющие нормальное распределение, их дисперсии неизвестны, но предполагается, что они равны. Есть основание высказать предположение, что генеральные средние данных

совокупностей	равны.	Выдвигается	гипотеза		Н0: М(Х) = М(Y).
Конкурирующая	гипотеза	может быть одной		из трех:	Н1: М(Х) М(Y)
(критическая область правосторонняя);			Н1: М(Х) М(Y) (критическая
область двусторонняя		и Н1: М(Х) М(Y)		(критическая область
левосторонняя).
Гипотеза Н0 проверяется по выборочным данным с помощью
случайной величины

в

в

nx ny (nx + ny 2)

T

x

y

,

(n

x

1)S 2 (n

y

1)S 2

nx ny

x

y

которая имеет

распределение

Стьюдента с k = nx + ny – 2 степенями

свободы.

Для проверки гипотезы делаются выборки объемами nx и ny

соответственно.

По выборочным

данным

рассчитываются несмещенные

точечные оценки генеральных средних: xв и yв , генеральных дисперсий: S x2 и S y2 . Далее рассчитывают наблюдаемое значение критерия Тнабл , а по

таблице критических точек распределения Стьюдента находят tкрит( , k). Затем сравнивают Тнабл и tкрит( , k) и делают вывод.

Примечание. Если в условии задачи неизвестно ничего о генеральных дисперсиях, то предварительно проверяется вспомогательная гипотеза о равенстве генеральных дисперсий. Если получим, что дисперсии равны, то далее проверяется основная гипотеза по критерию Стьюдента, в противном случае решение задачи прекращается.

29

При формулировке вывода руководствуются следующим правилом:

Если наблюдаемое значение критерия попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу, по данным наблюдения М(Х) = М(Y), расхождение между выборочными средними

случайное;

если наблюдаемое значение критерия попало в критическую область, то

нулевая гипотеза отвергается, справедлива конкурирующая гипотеза, расхождение между выборочными средними значимо.

Проверка гипотезы о равенстве вероятностей

По отношению к событию А проводят n независимых испытаний с вероятностью р при каждом испытании. Эта вероятность неизвестна, но есть основание предположить, что она равна некоторой величине р0, называемой гипотетической вероятностью. Чтобы проверить это предположение,

находят статистическую вероятность mn , она, как правило, отличается от

гипотетической вероятности. Выдвигается нулевая гипотеза Н0: р = р0. Конкурирующая гипотеза может быть трех видов:

Н1: р р0 (критическая область правосторонняя); Н1: р р0 (критическая область левосторонняя); Н1: р р0 (критическая область двусторонняя).

Нулевая гипотеза проверяется по выборочным данным с помощью случайной величины, имеющей нормированное нормальное распределение:

U m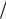n p0 n , где q0 = 1 – p0 .

p0 q0

По данным наблюдения вычисляется наблюдаемое значение критерия Uнабл . Критическое значение критерия находится с помощью функции Лапласа с учетом вида критической области, а именно:

1)Н1: р р0 , тогда Ф(Uкрит.пр) = 12 ;

2)Н1: р р0 , Uкрит.лев = –Uкрит.пр, так как случайная величина U имеет нормированное нормальное распределение;

3)Н1: р р0 , в этом случае Ф(Uкрит.дв) = 12 2 .

Далее сравниваем Uкрит и Uнабл.

30